Решение систем линейных уравнений с помощью обратной матрицы.

Пусть в системе(I) (см. §1) m=n и основная матрица системы невырожденная 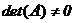. Запишем систему (I) в матричном виде (см. §2):

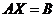, (2)

т.к. матрица A невырожденная, то она имеет обратную матрицу 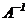(см. теорему 1 §6 главы 1). Умножим обе части равенства (2) на матрицу 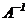, тогда

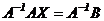. (3)

По определению обратной матрицы 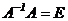. Из равенства (3) имеем

,

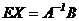отсюда

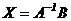. (4)

Пример 1.

Решить систему с помощью обратной матрицы

.

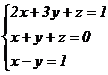Обозначим

; ; .

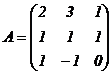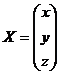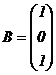В примере (§ 3)мы вычислили определитель 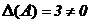, следовательно, матрица A имеет обратную матрицу 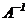. Тогда в силу (4)

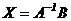, т.е.

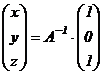. (5)

Найдем матрицу 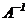(см. §6 главы 1)

, , ,

, , ,

, , ,

,

.

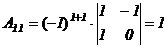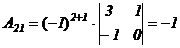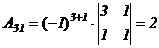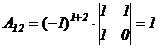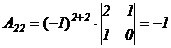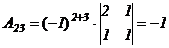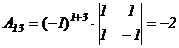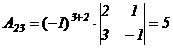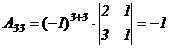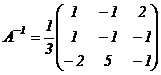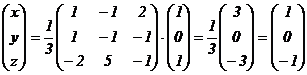Ответ: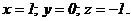

Метод Гаусса.

Пусть задана система линейных уравнений:

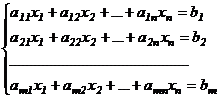. (I)

Требуется найти все решения системы (I) или убедиться в том, что система несовместна.

Определение 1. Назовем элементарным преобразованием системы (I) любое из трёх действий :

1) вычёркивание нулевого уравнения;

2) прибавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на число l;

3) перемена местами слагаемых в уравнениях системы так, чтобы неизвестные с одинаковыми номерами во всех уравнениях занимали одинаковые места, т.е. если, например, в 1-ом уравнении мы поменяли 2-ое и 3-е слагаемые, тогда то же самое необходимо сделать во всех уравнениях системы.

Метод Гаусса состоит в том, что система (I) с помощью элементарных преобразований приводится к равносильной системе, решение которой находится непосредственно или устанавливается её неразрешимость.

Как было описано в §2 система (I) однозначно определяется своей расширенной матрицей и любое элементарное преобразование системы (I) соответствует элементарному преобразованию расширенной матрицы :

.

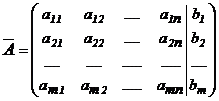Преобразование 1) соответствует вычёркиванию нулевой строки в матрице 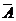, преобразование 2) равносильно прибавлению к соответствующей строке матрицы 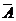другой её строки, умноженной на число l, преобразование 3) эквивалентно перестановке столбцов в матрице .

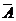Легко видеть, что, наоборот, каждому элементарному преобразованию матрицы 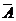соответствует элементарное преобразование системы (I). В силу сказанного, вместо операций с системой (I) мы будем работать с расширенной матрицей этой системы.

В матрице 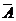1-ый столбец состоит из коэффициентов при х₁, 2-ой столбец - из коэффициентов при х₂ и т.д. В случае перестановки столбцов следует учитывать, что это условие нарушается. Например, если мы поменяем 1-ый и 2-ой столбцы местами, то теперь в 1-ом столбце будут коэффициенты при х₂, а во 2-ом столбце - коэффициенты при х₁.

Будем решать систему (I) методом Гаусса.

1. Вычеркнем в матрице 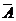все нулевые строки, если такие имеются (т.е. вычеркнем в системе (I) все нулевые уравнения).

2. Проверим, есть ли среди строк матрицы 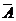строка, в которой все элементы, кроме последнего, равны нулю (назовём такую строку несовместной). Очевидно, что такой строке соответствует несовместное уравнение в системе (I) , следовательно, система (I) решений не имеет и на этом процесс заканчивается.

3. Пусть матрица 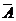не содержит несовместных строк (система (I) не содержит несовместных уравнений). Если a₁₁=0, то находим в 1-ой строке какой-нибудь элемент (кроме последнего) отличный от нуля и переставляем столбцы так, чтобы в 1-ой строке на 1-ом месте не было нуля. Будем теперь считать, что 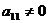(т.е. поменяем местами соответствующие слагаемые в уравнениях системы (I)).

4. Умножим 1-ую строку на 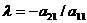и сложим результат со 2-ой строкой, затем умножим 1-ую строку на 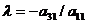и сложим результат с 3-ей строкой и т.д. Очевидно, что этот процесс эквивалентен исключению неизвестного x₁ из всех уравнений системы (I), кроме 1-ого. В новой матрице 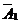получаем нули в 1-ом столбце под элементом a₁₁ :

.

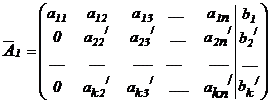5. Вычеркнем в матрице 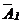все нулевые строки, если они есть, проверим, нет ли несовместной строки (если она имеется, то система несовместна и на этом решение заканчивается). Проверим, будет ли a₂₂ ^/=0, если да, то находим во 2-ой строке элемент, отличный от нуля и переставляем столбцы так, чтобы 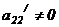. Далее умножаем элементы 2-ой строки на 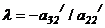и складываем с соответствующими элементами 3-ей строки, затем - элементы 2-ой строки на 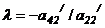и складываем с соответствующими элементами 4-ой строки и т.д., пока не получим нули под a₂₂ ^/

.

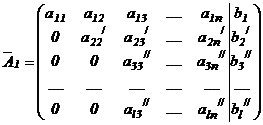Произведенные действия эквивалентны исключению неизвестного х₂ из всех уравнений системы (I), кроме 1-ого и 2-ого. Так как число строк конечно, поэтому через конечное число шагов мы получим, что либо система несовместна, либо мы придём к ступенчатой матрице (см. определение 2 §7 главы 1) :

,

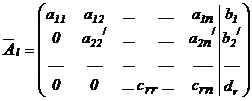где

.

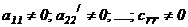Выпишем систему уравнений, соответствующую матрице 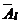. Эта система равносильна системе (I)

.

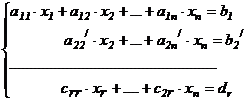Из последнего уравнения выражаем 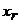; подставляем 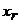в предыдущее уравнение, находим 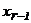и т.д., пока не получим .

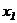Замечание 1. Таким образом, при решении системы (I) методом Гаусса мы приходим к одному из следующих случаев.

1. Система (I) несовместна.

2. Система (I) имеет единственное решение, если в матрице 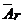число строк равно числу неизвестных ( ).

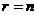3. Система (I) имеет бесчисленное множество решений, если число строк в матрице 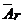меньше числа неизвестных ( ).

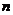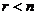Отсюда имеет место следующая теорема.

Теорема. Система линейных уравнений либо несовместна, либо имеет единственное решение, либо – бесконечное множество решений.

Примеры. Решить систему уравнений методом Гаусса или доказать ее несовместность:

а) ;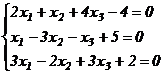

б) ;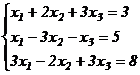

в) .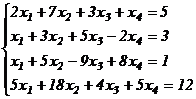

Решение.

а) Перепишем заданную систему в виде:

.

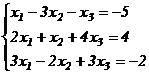Мы поменяли местами 1-ое и 2-ое уравнение исходной системы, чтобы упростить вычисления (вместо дробей мы с помощью такой перестановки будем оперировать только целыми числами).

Составляем расширенную матрицу:

.

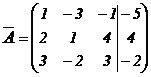Нулевых строк нет; несовместных строк нет, 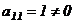; исключим 1-ое неизвестное 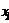из всех уравнений системы, кроме 1-го. Для этого умножим элементы 1-ой строки матрицы 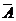на «-2» и сложим с соответствующими элементами 2-ой строки, что равносильно умножению 1-го уравнения на «-2» и сложению со 2-ым уравнением. Затем умножим элементы 1-ой строки на «-3» и сложим с соответствующими элементами третьей строки, т.е. умножим 2-ое уравнение заданной системы на «-3» и сложим с 3-им уравнением. Получим

.

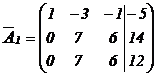Матрице 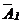соответствует система уравнений

.

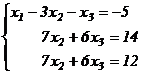В матрице 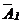нулевых строк нет, несовместных строк также нет, исключим неизвестное 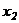из 3-го уравнения системы, для этого умножим элементы 2-ой строки матрицы 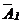на «-1» и сложим с элементами 3-ей строки :

.

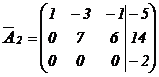Матрица 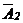содержит несовместную строку (в 3-ей строке все элементы равны нулю, кроме последнего). Этой строке соответствует несовместное уравнение 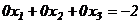. Следовательно, система решений не имеет ( 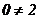), система несовместна.

б) Составляем расширенную матрицу:

.

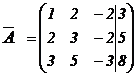Нулевых строк нет, несовместных строк нет, 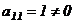, исключаем неизвестное 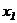из 2-го и 3-го уравнения заданной системы, для этого умножим элементы 1-ой строки матрицы 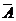на «-2», затем на «-3» и сложим соответственно с элементами 2-ой и 3-ей строк, получим

.

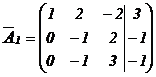Рекомендуем читателю проанализировать, какие операции при этом совершаются с заданной системой уравнений. Умножаем элементы 2-ой строки матрицы 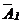на «-1» и складываем с элементами 3-ей строки, получаем:

,

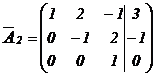где 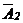- матрица ступенчатого вида.

Записываем систему уравнений, соответствующую этой матрице

.

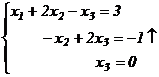Теперь двигаемся снизу вверх. Из последнего уравнения находим .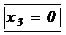

Подставляя это равенство в предпоследнее уравнение, находим .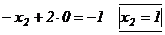

Подставляя 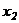и 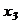в первое уравнение, получаем : .

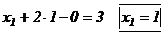Ответ: 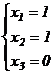- система имеет единственное решение.

в) Составляем расширенную матрицу:

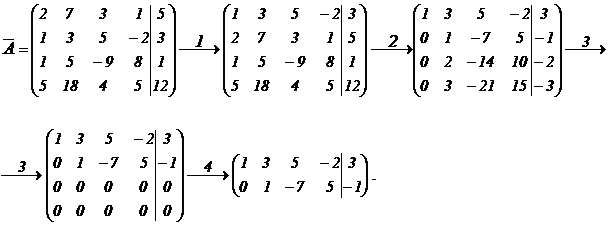
1. Переставим местами 1-ую и 2-ую строку для упрощения вычислений (меняем местами уравнения в заданной системе).

2. Умножим элементы 2-ой строки матрицы последовательно на «-2», «-1» и «-5» и сложим соответственно с элементами 2-ой, 3-ей и 4-ой строк (для получения нулей под элементом ).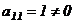

3. Аналогичным образом, получаем нули под элементом .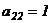

4. Вычеркиваем нулевые строки.

Последняя матрица – ступенчатая. Переходим от нее к системе уравнений:

;

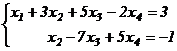из последнего уравнения получаем:

,

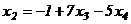подставляя это равенство в 1-ое уравнение системы, находим

.

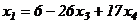Ответ: 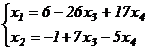- система имеет бесчисленное множество решений. Давая произвольные значения переменным 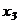и 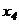, мы каждый раз будем получать частные решения заданной системы уравнений.

Замечание . Количество уравнений в окончательной системе при решении методом Гаусса всегда равно рангу матрицы 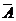- 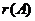(см. определение 3§7 главы 1).