V. Дифференциальные уравнения.
Для решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами вида
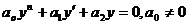 (1)
(1)
Составляют характеристическое квадратное уравнение
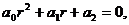 (2)
(2)
Которое получается из уравнения (1) заменой в нем производных искомой функции у соответствующими степенями r, причем сама функция у заменяется единицей. Тогда общее решение уравнения (1) строится в зависимости от дискриминанта Д квадратного уравнения (2).
Практика показывает, что наиболее трудным является случай Д<0, когда уравнение (2) имеет пару сопряженных комплексных корней
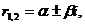 где
где  а α и β – действительные числа, причем β>0. Общее решение в этом случае таково:
а α и β – действительные числа, причем β>0. Общее решение в этом случае таково: 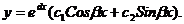
Задача 1. Найти α и β, если корни уравнения (2) имеют вид:
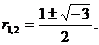
Решение: Преобразуем выражения для 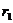 и
и 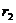 :
:
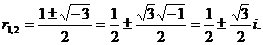
Нетрудно видеть, что 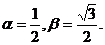
В частном случае, если 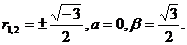
Задача 2. Найти частное решение уравнения 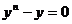 , удовлетворяющее начальным условиям у(0)=0,
, удовлетворяющее начальным условиям у(0)=0, 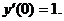
Решение: Данная задача с начальными условиями носит название задачи Коши. Составим характеристическое уравнение: r2-1=0. Его решениями являются 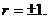 Общее решение уравнения в этом случае (Д>0) находится по формуле
Общее решение уравнения в этом случае (Д>0) находится по формуле 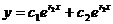 , т.е.
, т.е. 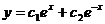 . (3)
. (3)
Найдем 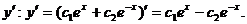 (4)
(4)
Подставим в уравнения (3) и (4) начальные условия:
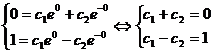
Решая эту систему, получаем 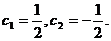 Найденные значения постоянных с1 и с2 подставляем в общее решение (3) и получаем искомое решение
Найденные значения постоянных с1 и с2 подставляем в общее решение (3) и получаем искомое решение 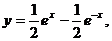 или
или 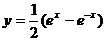
Вопросы для самопроверки:
1. Какое уравнение называется дифференциальным? Что такое порядок дифференциального уравнения?
2. Что называется решением дифференциального уравнения? Какое из решений называется общим, а какое частным?
3. Сформулируйте понятие задачи Коши.
4. Какое уравнение называется дифференциальным уравнением первого порядка с разделяющимися переменными? Как оно интегрируется?
5. Приведите формулы общих решений линейных однородных дифференциальных уравнений второго порядка.
Задачи для самоконтроля
Решить уравнения:
1. а) 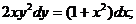 б)
б) 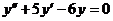 при условиях y(0)=1;
при условиях y(0)=1; 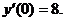
2. а) 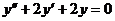 б)
б) 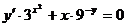 при условии y(0)=1.
при условии y(0)=1.
3. а) 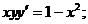 б)
б) 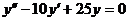 при условиях y(0)=0;
при условиях y(0)=0; 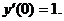
4. а) 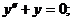 б)
б) 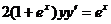 при условии y(0)=0.
при условии y(0)=0.
5. а) 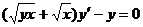 б)
б) 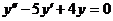 при условиях y(0)=5;
при условиях y(0)=5; 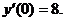
6. а) 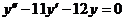 б)
б) 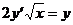 при условии y(4)=1.
при условии y(4)=1.
7. а) 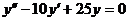 б)
б) 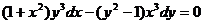 при условии y(1)=-1.
при условии y(1)=-1.
8. а) 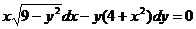 б)
б) 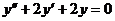 при условиях y(0)=1,
при условиях y(0)=1, 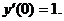
9. а) 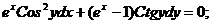 б)
б) 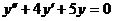 при условиях y(0)=-3,
при условиях y(0)=-3, 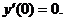
10. а) 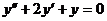 ; б)
; б) 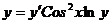 при условиях
при условиях 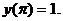
VI. Числовые и функциональные ряды.
Числовые ряды
Пусть задана бесконечная последовательность чисел 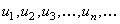 . Выражение
. Выражение
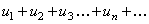
 (1)
(1)
называется числовым рядом. Числа 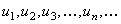 называются членами этого ряда. Член
называются членами этого ряда. Член 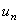 ряда (97), стоящий на
ряда (97), стоящий на 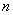 -м месте, считая от начала, называется общим членом этого ряда. Ряд (97) считается заданным, если известен общий член его, выраженный как функция номера
-м месте, считая от начала, называется общим членом этого ряда. Ряд (97) считается заданным, если известен общий член его, выраженный как функция номера 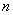 .
.
Выражение (1) удобно обозначать следующим образом: 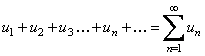 .
.
Сумма конечного числа n первых членов ряда называетсяn-ой частичной суммой ряда.
Рассмотрим частичные суммы: 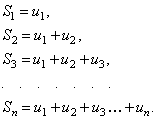
Если существует конечный предел 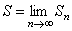 , то его называют суммой ряда (1) и говорят, что ряд (1) сходится.
, то его называют суммой ряда (1) и говорят, что ряд (1) сходится.
Если 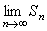 не существует (например
не существует (например 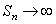 , при
, при 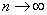 ), то говорят, что ряд (1) расходится и суммы не имеет.
), то говорят, что ряд (1) расходится и суммы не имеет.
Пример 1. Определить сходимость числового ряда
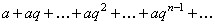 . (2)
. (2)

Решение. Данный числовой ряд – сумма всех членов геометрической прогрессии с первым членом 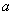 и знаменателем
и знаменателем 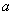
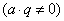 Вычисляя сумму первых
Вычисляя сумму первых 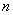 чисел, получаем:
чисел, получаем:
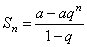 или
или 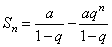 .
.
Переходя к вычислению предела, заметим, что в зависимости от значений 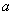 и
и 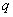 частичная сумма ряда принимает различные значения.
частичная сумма ряда принимает различные значения.
1). Если 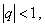 , то
, то 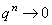 при
при 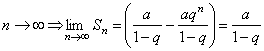 . Значит, в случае
. Значит, в случае 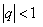 ряд (2) сходится и его сумма
ряд (2) сходится и его сумма 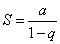 .
.
2). Если 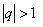 , то
, то 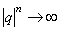 и тогда
и тогда 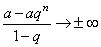 при
при 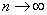 , т.е.
, т.е. 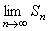 не существует. Таким образом, в случае
не существует. Таким образом, в случае 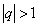 ряд (98) расходится.
ряд (98) расходится.
3) Если 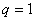 , то ряд (2) имеет вид:
, то ряд (2) имеет вид: 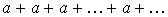 . В этом случае
. В этом случае 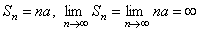 , т.е. ряд расходится.
, т.е. ряд расходится.
Если 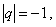 то
то 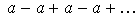 . В этом случае:
. В этом случае: 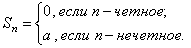
Следовательно, частичная сумма предела не имеет.
Таким образом, сумма членов геометрической прогрессии (с первым членом отличным от нуля) сходится только тогда, когда знаменатель прогрессии по абсолютной величине меньше единицы. ►
Теорема. Если сходится ряд, получившийся из данного ряда (1) отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов.
Теорема. Если ряд (97) сходится и его сумма равная S, то ряд
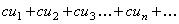 (3)
(3)
где 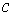 – произвольное действительное число, так же сходится и его сумма равна
– произвольное действительное число, так же сходится и его сумма равна 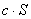 .
.
Теорема.
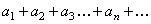 , (4)
, (4)
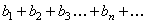 (5)
(5)
сходятся и их суммы, соответственно равны 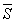 и
и 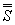 , то ряды
, то ряды
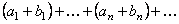 , (6)
, (6)
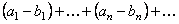 (7)
(7)
также сходятся и их суммы равные соответственно 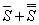 и
и 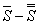 .
.
Теорема. (Необходимый признак сходимости ряда). Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n.
Следствие. Если n-й член ряда не стремится к нулю, то ряд расходится.
Пример 7.1.2. Определить сходимость числового ряда 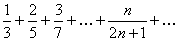 .
.
Решение. Воспользуемся необходимым признаком сходимости ряда. Для данного числового ряда записываем формулу общего члена и вычисляем предел
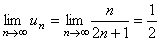 .
.
Так как предел не равен нулю, то исходный ряд расходится. ►
Подчеркнем, что рассмотренный признак является только необходимым, но не является достаточным, то есть из того, что n-й член ряда стремится к нулю, ещё не следует, что ряд сходится – ряд может и расходиться.
Пример 7.1.3. Определить сходимость числового ряда
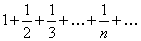 . (8)
. (8)
Решение. Для данного числового ряда записываем формулу общего члена и вычисляем предел 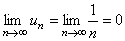 . Необходимый признаквыполнен.Докажем, однако,что исходный ряд расходится. Распишем его подробнее:
. Необходимый признаквыполнен.Докажем, однако,что исходный ряд расходится. Распишем его подробнее:
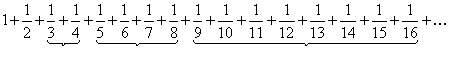 (9)
(9)
и составим вспомогательный ряд:
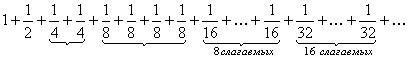 . (10)
. (10)
Ряд (106) строится следующим образом: его первый член равен 1, второй – 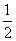 , третий и четвёртый равны
, третий и четвёртый равны 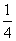 , члены с пятого по восьмой равны
, члены с пятого по восьмой равны 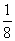 , члены с девятого по 16-й равны
, члены с девятого по 16-й равны 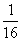 , с 17-го по 32-й –
, с 17-го по 32-й – 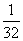 , и т.д.
, и т.д.
Обозначим через Sn(1) сумму первых n членов гармонического ряда (105), а через Sn(2) сумму первых n членов ряда (106). Так как каждый член ряда (105) больше соответствующего члена ряда (106), то для (n > 2) выполнено
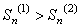 . (11)
. (11)
Подсчитаем частичные суммы ряда (106) для значений n равных степеням двойки: 21, 22, 23, 24, 25 и т.д. Имеем:
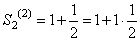 ,
,
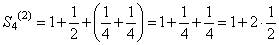 ,
,
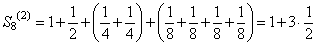 ,
,
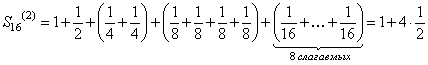 ,
,
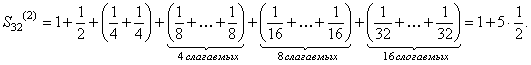
Заметим, что 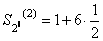 ,
, 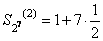 , и т.д. Следовательно
, и т.д. Следовательно 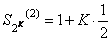 , т.е. частичные суммы Sn(2) при
, т.е. частичные суммы Sn(2) при 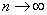 неограниченно увеличиваются или
неограниченно увеличиваются или 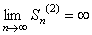 . Но тогда из соотношения (11) следует, что
. Но тогда из соотношения (11) следует, что 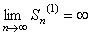 . Таким образом, исходный числовой ряд расходится. Числовой ряд (8) часто называют гармоническим. ►
. Таким образом, исходный числовой ряд расходится. Числовой ряд (8) часто называют гармоническим. ►
Пусть даны два ряда с положительными членами
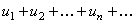 , (12)
, (12)
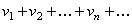 . (13)
. (13)
Для них справедливы следующие утверждения.
Теорема (Первый признак сравнения числовых рядов). Пусть члены ряда (12) не больше соответствующих членов ряда (13), т.е. при n=1, 2, ...
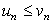 . (14)
. (14)
Тогда, если ряд (109) сходится, то сходится и ряд (12).
Пример 7.1.4. Определить сходимость числового ряда 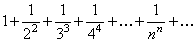 .
.
Решение. Поскольку все слагаемые данного числового ряда положительны, воспользуемся теоремой первым признаком сравнения. Все члены исходного ряда больше соответствующих членов ряда 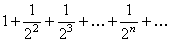 , члены которого образуют геометрическую прогрессию со знаменателем
, члены которого образуют геометрическую прогрессию со знаменателем 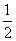 . В примере.1 было показано, что такие числовые ряды (
. В примере.1 было показано, что такие числовые ряды ( 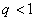 ) сходятся. Более того, сумма этого ряда равна
) сходятся. Более того, сумма этого ряда равна 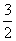 и, следовательно, сумма первоначального ряда не больше чем
и, следовательно, сумма первоначального ряда не больше чем 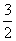 .►
.►
Теорема (Второй признак сравнения числовых рядов). Пусть члены ряда (108) не меньше соответствующих членов ряда (14), т.е. при n=1, 2, ...
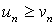 . (15)
. (15)
Тогда, если ряд (12) расходится, то расходится и ряд (13).
Пример 7.1.5. Определить сходимость числового ряда 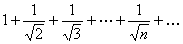 .
.
Решение. Поскольку все слагаемые данного числового ряда положительны, воспользуемся вторым признаком сравнения. Так как 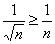 , то члены данного ряда больше соответствующих членов гармонического ряда
, то члены данного ряда больше соответствующих членов гармонического ряда 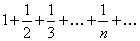 , который расходится (см. пример 3). Поэтому исходный числовой ряд также расходится. ►
, который расходится (см. пример 3). Поэтому исходный числовой ряд также расходится. ►
Теорема (Признак сходимости Даламбера).Пусть дан числовой ряд (97) с положительными членами. Если отношение (n+1)-го члена к n-му члену при 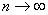 имеет конечный предел, т.е.
имеет конечный предел, т.е.
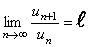 , (16)
, (16)
то 1) при 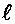 <1 – ряд сходится;
<1 – ряд сходится;
2) при 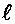 >1 – ряд расходится.
>1 – ряд расходится.
Замечание. Ряд будет расходиться и в том случае, когда 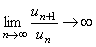 . Это следует из того, что если
. Это следует из того, что если 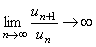 , то, начиная с некоторого номера n=N, будет иметь место неравенство:
, то, начиная с некоторого номера n=N, будет иметь место неравенство: 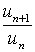 >1. Следовательно,
>1. Следовательно, 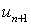 >
> 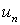 .
.
Пример 7.1.6. Исследовать сходимость ряда 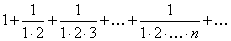
Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим отношение 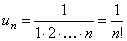 ,
, 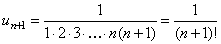 ,
, 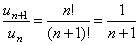 . Вычисляя предел, получим
. Вычисляя предел, получим
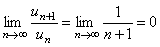 <1.
<1.
Таким образом, исходный ряд сходится. ►
Пример 7.1.7. Исследовать сходимость ряда 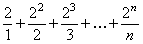 .
.
Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим отношение 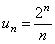 ,
, 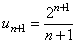 ,
, 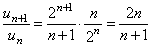 . Вычисляя предел, получим
. Вычисляя предел, получим
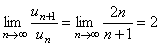 > 1.
> 1.
Таким образом, исходный ряд расходится. ►
Признак Даламбера дает ответ на вопрос о том сходится ли данный положительный ряд в случае, когда 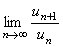 существует и отличен от 1. Если же этот предел не существует или
существует и отличен от 1. Если же этот предел не существует или 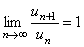 , то признак Даламбера не дает возможности установить, сходится ряд или расходится, так как в этом случае ряд может оказаться или сходящимся, или расходящимся. Для решения вопроса о сходимости надо применить какой-либо другой признак.
, то признак Даламбера не дает возможности установить, сходится ряд или расходится, так как в этом случае ряд может оказаться или сходящимся, или расходящимся. Для решения вопроса о сходимости надо применить какой-либо другой признак.
Если 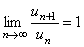 , но отношение
, но отношение 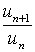 для всех номеров n, начиная с некоторого больше 1, то ряд расходится. Это следует из того, что если
для всех номеров n, начиная с некоторого больше 1, то ряд расходится. Это следует из того, что если 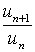 >1, то
>1, то 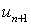 >
> 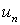 и общий член ряда не стремится к 0 при n®¥.
и общий член ряда не стремится к 0 при n®¥.
Пример 7.1.8. Исследовать сходимость ряда 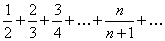 .
.
Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим предел отношения
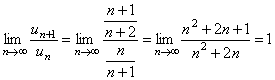 .
.
В данном случае ряд расходится, так как 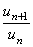 >1 для всех n. Действительно,
>1 для всех n. Действительно,
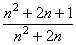 >1 Û
>1 Û 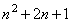 >
> 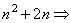 1>0. ►
1>0. ►
Пример 7.1.9. Определить сходимость числового ряда 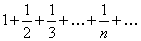 .
.
Решение. Применяя признак сходимости Даламбера к гармоническому ряду, получаем 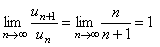 . Признак Даламбера в данном случае не дает ответа на вопрос о сходимости, но в примере 7.1.3 была установлена расходимость данного числового ряда. ►
. Признак Даламбера в данном случае не дает ответа на вопрос о сходимости, но в примере 7.1.3 была установлена расходимость данного числового ряда. ►
Пример 7.1.10. Исследовать сходимость ряда 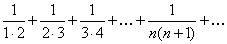 .
.
Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим предел отношения
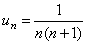 ,
, 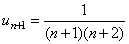 ,
, 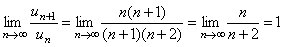 .
.
На основании признака Даламбера сходимость установить нельзя. Однако, так как 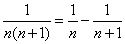 , то можно преобразовать данный ряд
, то можно преобразовать данный ряд
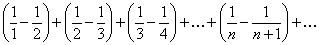
Вычисляя частичные суммы 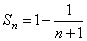 и предел, получаем
и предел, получаем
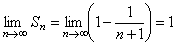 .
.
Таким образом, исходный ряд сходится. ►
Теорема (Признак Коши). Если для ряда с положительными членами (97) величина 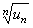 имеет конечный предел
имеет конечный предел 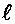 при
при 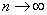 , т.е.
, т.е.
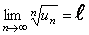 ,
,
то 1) при 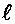 < 1 – ряд сходится;
< 1 – ряд сходится;
 2) при 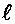 > 1 – ряд расходится.
> 1 – ряд расходится.
Замечание. Как и в признаке Даламбера, случай 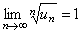 , требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся. Так для гармонического ряда имеем:
, требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся. Так для гармонического ряда имеем: 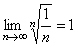 , но он расходится. Рассмотрим другой числовой ряд
, но он расходится. Рассмотрим другой числовой ряд 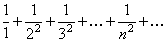 . Для него так же имеет место равенство
. Для него так же имеет место равенство 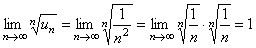 , но он сходится по первому признаку сходимости. Заметим, что если отбросить первый член, то члены оставшегося ряда будут меньше соответствующих членов ряда
, но он сходится по первому признаку сходимости. Заметим, что если отбросить первый член, то члены оставшегося ряда будут меньше соответствующих членов ряда 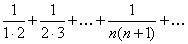 , который сходится (см. пример 7.1.10).
, который сходится (см. пример 7.1.10).
Пример 7.1.11. Исследовать сходимость ряда 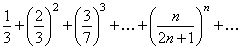
Решение. Воспользуемся признаком сходимости Коши. Определим формулу общего члена числового ряда и вычислим предел 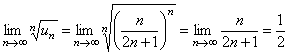 .
.
Так как предел конечен и меньше единицы, то по признаку Коши исходный числовой ряд сходится. ►
Приведем без доказательства признак сходимости числовых рядов с положительными членами, который удобно использовать, когда признаки Даламбера и Коши не дают ответа на вопрос о сходимости ряда.
Теорема (Интегральный признак сходимости).Пусть дан ряд 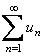 , члены которого положительны и не возрастают, т.е.
, члены которого положительны и не возрастают, т.е. 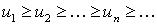 , а функция
, а функция 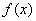 , определена при
, определена при 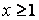 , непрерывная и не возрастающая и
, непрерывная и не возрастающая и 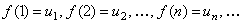 . Тогда для сходимости ряда
. Тогда для сходимости ряда 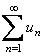 необходимо и достаточно, чтобы сходился несобственный интеграл
необходимо и достаточно, чтобы сходился несобственный интеграл 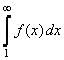 .
.
Пример 7.1.12. Исследовать сходимость обобщенного гармонического ряда 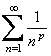 .
.
Решение. Пусть 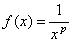 . Функция
. Функция 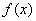 при
при 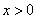 (а значит и при
(а значит и при 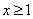 ) положительна и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла
) положительна и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла 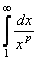 . Имеем
. Имеем 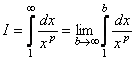 .
.
Если 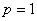 , то
, то 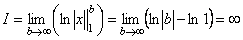 .
.
Если 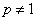 , то
, то 
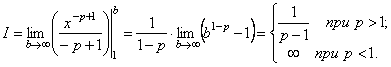
Итак, данный обобщенный гармонический ряд сходится при 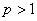 и расходится при
и расходится при 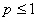 . ►
. ►
Знакочередующимся рядом называется ряд
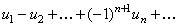 , (17)
, (17)
где 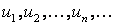 , – положительные числа.
, – положительные числа.
Теорема (Признак Лейбница). Если в знакочередующемся ряде (17) члены таковы, что
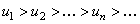 (18)
(18)
и
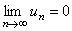 (19)
(19)
то ряд (17) сходится, его сумма положительна и не превосходит первого члена.
Замечание. Теорема Лейбница справедлива, если неравенства выполняются, начиная с некоторого номера N.
Теорема Лейбница иллюстрируется геометрически следующим образом. На числовой прямой будем откладывать (рис. 21)частичные суммы:
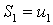 ,
, 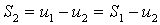 ,
, 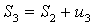 ,
, 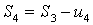 , …
, …
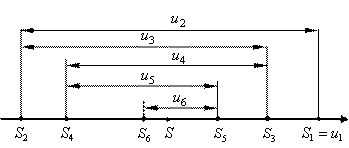
Рис. 21. Геометрический смысл теоремы Лейбница
Тогда точки, соответствующие частичным суммам будут приближаться к некоторой точке S. При этом точки, соответствующие чётным суммам располагаются слева от S, а нечетным суммам – справа от S.
Пример 7.1.13. Исследовать сходимость ряда 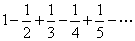 .
.
Решение. Поскольку данный ряд является знакочередующимся, воспользуемся признаком сходимости Лейбница. Определим формулу общего члена числового ряда и проверим условия теоремы. Имеем:
1) 1 > 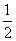 >
> 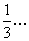 ;
;
2) 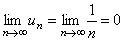 .
.
Так как оба условия выполнены, то исходный ряд сходится по признаку Лейбница. ►
Пример 7.1.14. Исследовать сходимость ряда 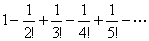
Решение. Поскольку данный ряд является знакочередующимся, воспользуемся признаком Лейбница. Определим формулу общего члена числового ряда и проверим условия теоремы. Имеем:
3) 1 > 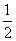 >
> 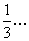 ;
;
4) 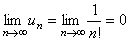 .
.
Так как оба условия выполнены, то исходный ряд сходится по признаку Лейбница. ►
Ряд называется знакопеременным, если среди его членов имеются как положительные так и отрицательные.
Знакочередующиеся ряды являются частным случаем знакопеременных рядов.
Теорема. Если знакопеременный ряд
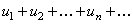 (20)
(20)
таков, что ряд, составленный из абсолютных величин его членов
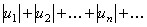 (21)
(21)
сходится, то, и данный знакопеременный ряд также сходится.
Пример 7.1.15. Исследовать сходимость ряда
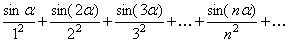 (22)
(22)
где a – любое число.
Решение. Наряду с данным рядом, рассмотрим два следующих ряда:
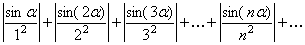 , (23)
, (23)
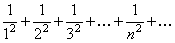 (24)
(24)
Ряд (24) сходится (см. замечание к теореме Коши). Так как члены ряда (23) не больше соответствующих членов ряда (24), т.е.
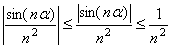 ,
,
то по первому признаку сравнения ряд (23) сходится. Следовательно, по теореме ряд (22) так же сходится. ►
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд называется условно сходящимся.
Пример 7.1.16. Исследовать сходимость ряда 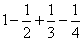 .
.
Решение. Данныйзнакопеременный ряд является условно сходящимся, так как ряд, составленный из абсолютных величин его членов, есть гармонический ряд 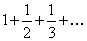 , который расходится. Сам же ряд сходится (см. пример 7.1.13) по признаку Лейбница. ►
, который расходится. Сам же ряд сходится (см. пример 7.1.13) по признаку Лейбница. ►
Пример 7.1.17. Исследовать сходимость ряда 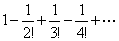 .
.
Решение. Данный знакопеременный ряд абсолютно сходящийся, так как ряд, составленный из абсолютных величин его членов
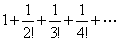
сходится (см. пример 7.1.6). ►
Теорема. (Погрешности при вычислении сумм сходящегося знакопеременного ряда). Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
Теорема. Если ряд сходится условно, то какое бы мы не задали число А, можно так переставить его члены, чтобы его сумма оказалась в точности равной А. Более того, можно так переставить члены условно сходящегося ряда, чтобы ряд, полученный после перестановки, оказался расходящимся.
Пример 7.1.18. Исследовать сходимость ряда
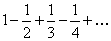 (25)
(25)
Решение. Докажем, что данный знакопеременный ряд сходится не абсолютно. Обозначим его сумму через 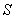 . Очевидно, что
. Очевидно, что 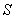 >0. Сделаем перестановку членов этого ряда следующим образом:
>0. Сделаем перестановку членов этого ряда следующим образом:
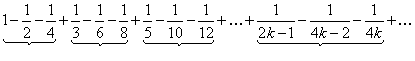 . (122)
. (122)
Покажем, что полученный ряд сходится, но его сумма 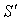 в два раза меньше суммы ряда (25), т.е. равна
в два раза меньше суммы ряда (25), т.е. равна 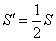 . Обозначим через
. Обозначим через 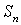 и
и 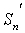 частичные суммы рядов (25) и (26). Рассмотрим сумму 3k членов ряда (26):
частичные суммы рядов (25) и (26). Рассмотрим сумму 3k членов ряда (26):
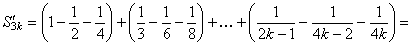
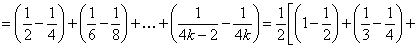
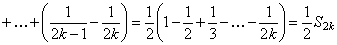 .
.
Вычислим предел суммы 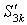 , учитывая, что сумма ряда (25) равна
, учитывая, что сумма ряда (25) равна 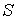 :
:
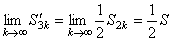 .
.
Заметим, что
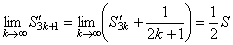 ,
,
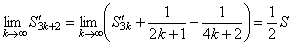 .
.
Таким образом, 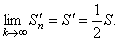 т.е. в данном случае сумма ряда (26) изменилась после перестановки его членов (уменьшилась в 2 раза). ►
т.е. в данном случае сумма ряда (26) изменилась после перестановки его членов (уменьшилась в 2 раза). ►
Функциональные ряды
Ряд
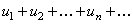
называется функциональным, если его члены являются функциями от х, т.е. 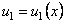 ,
, 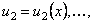
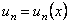 , которые определены на некотором множестве X.
, которые определены на некотором множестве X.
Если переменной 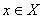 придавать различные числовые значения, то будут получаться сходящиеся или расходящиеся числовые ряды. Совокупность таких значений переменной х, при которых функциональный ряд сходится, называют областью сходимости. Областью сходимости ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.
придавать различные числовые значения, то будут получаться сходящиеся или расходящиеся числовые ряды. Совокупность таких значений переменной х, при которых функциональный ряд сходится, называют областью сходимости. Областью сходимости ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.
По аналогии с числовыми рядами определяются частичные суммы функционального ряда, предел которых определяет сумму ряда (если существует). Очевидно, что сумма функционального ряда в области сходимости является функцией от х, т.е.
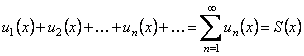 .
.
Говорят, что последовательность функций 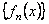 сходится равномерно к функции
сходится равномерно к функции 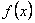 на множестве D, если для любого
на множестве D, если для любого 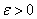 можно определить такой номер N, зависящий только от
можно определить такой номер N, зависящий только от 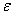 , что для любого
, что для любого 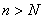 и для всех
и для всех 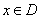 выполняется неравенство
выполняется неравенство
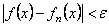 .
.
Ряд 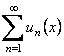 сходится равномерно на множестве D к сумме
сходится равномерно на множестве D к сумме 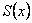 , если последовательность его частичных сумм
, если последовательность его частичных сумм 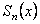 сходится равномерно на множестве D к функции
сходится равномерно на множестве D к функции 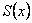 .
.
Приведем достаточный признак равномерной сходимости, который удобен в практическом применении.
Теорема (Признак Вейрштрассе). Если для членов функционального ряда 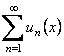 выполняются неравенства
выполняются неравенства
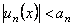 ,
,
где 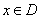 , а
, а 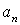 – некоторые числа, не зависящие от х, и при этом числовой ряд
– некоторые числа, не зависящие от х, и при этом числовой ряд 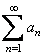 сходится, то ряд
сходится, то ряд 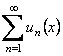 сходится на множестве D равномерно.
сходится на множестве D равномерно.
Следующие теоремы устанавливают основные свойства равномерно сходящихся функциональных рядов.
Теорема. Если функции 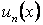 определены и непрерывны на множестве D, а ряд
определены и непрерывны на множестве D, а ряд 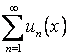 на этом же множестве сходится равномерно к сумме
на этом же множестве сходится равномерно к сумме 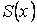 , то эта сумма будет непрерывной на D функцией.
, то эта сумма будет непрерывной на D функцией.
Теорема. Если функции 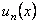 определены и непрерывны на множестве
определены и непрерывны на множестве 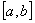 , а функциональный ряд
, а функциональный ряд 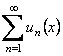 на этом же множестве сходится равномерно к сумме
на этом же множестве сходится равномерно к сумме 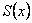 , то его можно почленно интегрировать на
, то его можно почленно интегрировать на 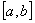 , т.е.
, т.е.
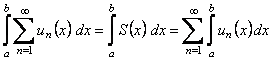 .
.
Теорема. Пусть функции 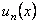 определены на
определены на 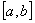 и имеют непрерывные первые производные
и имеют непрерывные первые производные 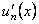 на
на  . Если функциональный ряд
. Если функциональный ряд 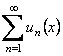 сходится на отрезке
сходится на отрезке 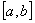 , а функциональный ряд
, а функциональный ряд 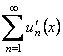 равномерно сходится на
равномерно сходится на 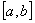 к сумме
к сумме 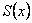 , то
, то 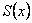 имеет на
имеет на  производную, причем
производную, причем
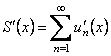 .
.
Заметим, что условия теорем достаточно жесткие, т.е. нельзя просто интегрировать и, особенно, дифференцировать функциональные ряды почленно. Это может привести к неверным результатам.
Степенным рядом называется функциональный ряд вида:
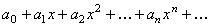 (123)
(123)
где 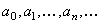 – постоянные числа, называемые коэффициентами ряда.
– постоянные числа, называемые коэффициентами ряда.
Теорема (Абеля)
1) Если степенной ряд сходится при некотором значении 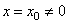 , то абсолютно сходится при всяком значении
, то абсолютно сходится при всяком значении 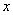 , для которого справедливо
, для которого справедливо 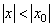 .
.
2) Если степенной ряд расходится при некотором значении 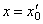 , то он расходится при всяком
, то он расходится при всяком 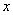 :
: 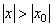 .
.
Заметим, что теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда. Действительно, если точка х0 – точка сходимости, то интервал 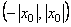 заполнен точками абсолютной сходимости. Если
заполнен точками абсолютной сходимости. Если 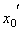 – точка расходимости, то вся бесконечная полупрямая вправо от точки
– точка расходимости, то вся бесконечная полупрямая вправо от точки 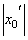 и вся полупрямая влево от точки –
и вся полупрямая влево от точки – 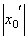 состоит из точек расходимости. Из этого можно заключить, что существует число R>0, что при
состоит из точек расходимости. Из этого можно заключить, что существует число R>0, что при 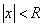 мы имеем точки абсолютной сходимости, а при
мы имеем точки абсолютной сходимости, а при 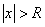 – точки расходимости.Интервалом сходимости степенного ряда называется такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится при том абсолютно, а для точек х, лежащих вне его, ряд расходится (рис. 22). Число R называется радиусом сходимости степенного ряда.
– точки расходимости.Интервалом сходимости степенного ряда называется такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится при том абсолютно, а для точек х, лежащих вне его, ряд расходится (рис. 22). Число R называется радиусом сходимости степенного ряда.
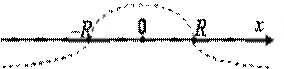
Рис. 22. Интервал сходимости степенного ряда
На концах интервала (т.е. при х = R, х = –R) вопрос о сходимости или расходимости остается не ясным. И для конкретного ряда решается индивидуально. Отметим, что у некоторых рядов интервал сходимости вырождается в точку R = 0, у дру
