III. Введение в математический анализ. Дифференциальное исчисление функции.
Тема 1. Введение в математический анализ.Область определения функции 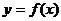 совпадает с ОДЗ (областью допустимых значений) правой части
совпадает с ОДЗ (областью допустимых значений) правой части 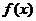 , т.е. с множеством всех значений х, при которых
, т.е. с множеством всех значений х, при которых 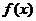 вычисляется.
вычисляется.
Задача 1. Найти область определения функции 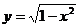
Решение. Первая часть вычисляется при всех значениях х, для которых подкоренное выражение неотрицательно. Поэтому область определения D(y) будет найдена из условия 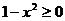 . Решая это неравенство, получаем
. Решая это неравенство, получаем 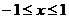 , т.е.
, т.е. 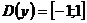
При анализе функции полезно проверить, обладает ли она свойством четности или нечетности. Наличие этих свойств позволяет упростить построение графика функции. Достаточно построить график функции для 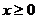 . Тогда для четной функции часть графика для
. Тогда для четной функции часть графика для 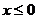 получается симметричным отображением построенного графика относительно оси Оу, а для нечетной – относительно начала координат.
получается симметричным отображением построенного графика относительно оси Оу, а для нечетной – относительно начала координат.
Задача 2. Выяснить, обладают ли данные функции свойством четности или нечетности:
а) 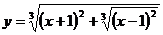 б)
б) 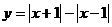 .
.
Решение.
а) 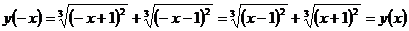 .
.
Итак, 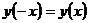 и, следовательно, функция является четной.
и, следовательно, функция является четной.
б) 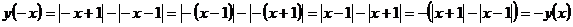 , т.е.
, т.е. 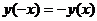 и, следовательно, функция у(х) является нечетной. Здесь использовано свойство модуля (абсолютной величины) числа:
и, следовательно, функция у(х) является нечетной. Здесь использовано свойство модуля (абсолютной величины) числа: 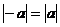 .
.
Вопросы для самопроверки:
1. Что называется функцией?
2. Какие способы задания функции Вы знаете?
3. Какая функция называется четной, а какая нечетной?
Тема 2. Пределы
Функция называется непрерывной в точке 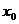 , если имеет место равенство:
, если имеет место равенство:
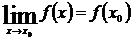 (1), которое помогает очень просто находить пределы непрерывных функций. Для вычисления предела такой функции находят ее значение в предельной точке
(1), которое помогает очень просто находить пределы непрерывных функций. Для вычисления предела такой функции находят ее значение в предельной точке 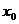 . К непрерывным относятся все элементарные функции, а также многочлены в любой точке их области определения.
. К непрерывным относятся все элементарные функции, а также многочлены в любой точке их области определения.
Например,
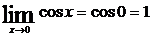 ;
; 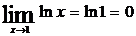
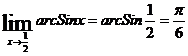 ;
; 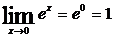
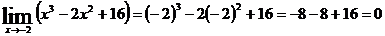
Если равенство (1) не выполняется, то функция разрывна в точке 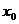 .
.
Но, если не существует значение 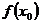 , это не означает, что не вычисляется предел функции при
, это не означает, что не вычисляется предел функции при 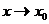 .
.
Задача 1. Найти 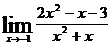
Решение:
Дробь при 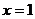 не вычисляется, причем
не вычисляется, причем 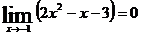 и
и 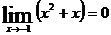 , т.е. дробь представляет собой отношение двух бесконечно малых функций (неопределенность вида
, т.е. дробь представляет собой отношение двух бесконечно малых функций (неопределенность вида 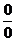 ). Для вычисления предела дроби (раскрытия неопределенности) следует разложить и числитель, и знаменатель на множители и при наличии одинакового множителя, стремящегося к 0 при
). Для вычисления предела дроби (раскрытия неопределенности) следует разложить и числитель, и знаменатель на множители и при наличии одинакового множителя, стремящегося к 0 при 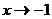 , дробь на этот множитель сократить:
, дробь на этот множитель сократить: 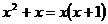 .
.
Для разложения на множители числителя необходимо вспомнить формулу 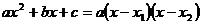 , где
, где 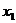 и
и 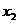 - действительные корни квадратного трехчлена,
- действительные корни квадратного трехчлена, 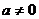 .
.
Для трехчлена 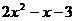 ,
, 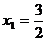 ,
, 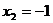 ,
, 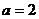 .
.
Поэтому 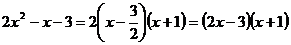 .
.
Для 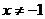 преобразования будут такими:
преобразования будут такими:
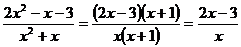 ;
;
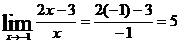 .
.
Задача 2. Найти 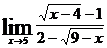 .
.
Решение:
При х=5 дробь не вычисляется, пределы числителя и знаменателя равны 0, т.е. имеем неопределенность вида 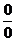 . Для раскрытия неопределенности следует избавиться от конкретных иррациональностей в числителе и знаменателе, а при наличии общего множителя дробь на него сократить. Достигается это с помощью следующих тождественных преобразований для
. Для раскрытия неопределенности следует избавиться от конкретных иррациональностей в числителе и знаменателе, а при наличии общего множителя дробь на него сократить. Достигается это с помощью следующих тождественных преобразований для 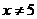 :
:
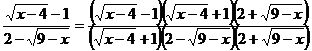 =
= 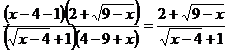 .
.
Теперь 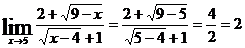 .
.
Хорошо известен 1 замечательный предел: 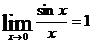 . Но часто аргументом синуса является функция
. Но часто аргументом синуса является функция 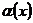 , стремящаяся к 0 при
, стремящаяся к 0 при 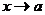 . В этом случае
. В этом случае 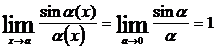 .
.
Задача 3. Найти 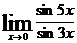 .
.
Решение: Дробьпри х=0 не вычисляется 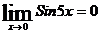 ,
, 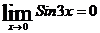 , имеем неопределенность вида
, имеем неопределенность вида 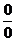 . Преобразуем дробь следующим образом:
. Преобразуем дробь следующим образом: 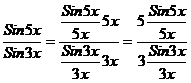 .
.
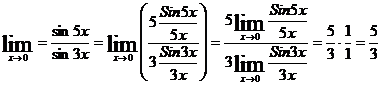 .
.
Следует отметить, что если функция 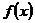 есть дробь, числитель который при
есть дробь, числитель который при 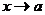 имеет предел, отличный от 0, а знаменатель, напротив, имеет пределом 0, то
имеет предел, отличный от 0, а знаменатель, напротив, имеет пределом 0, то 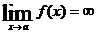 .
.
Задача 4. Найти 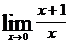 .
.
Решение: 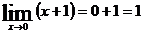 ,
, 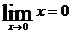 .
.
Следовательно, 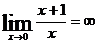 .
.
Задача 5. Найти 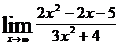 .
.
Решение: При 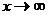 и числитель, и знаменатель – Бесконечно большие функции (неопределенность вида
и числитель, и знаменатель – Бесконечно большие функции (неопределенность вида 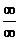 ). Для раскрытия неопределенности преобразуем дробь, разделив числитель на знаменатель на старшую степень
). Для раскрытия неопределенности преобразуем дробь, разделив числитель на знаменатель на старшую степень 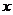 , т.е. на
, т.е. на 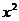 :
:
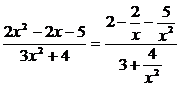 . Теперь
. Теперь 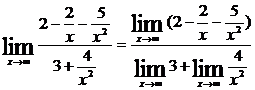 =
= 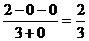
Задача 6. Найти 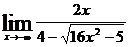 .
.
Решение: Имеем неопределенность вида 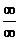 . Разделим числитель и знаменатель на
. Разделим числитель и знаменатель на 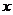 . Тогда:
. Тогда:
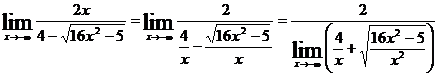
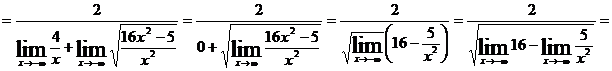
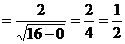 .
.
Здесь была использована формула: 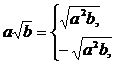
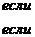
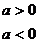 .
.
Задача7. Найти 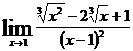 ,
,
Решение:
При 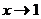 и числитель, и знаменатель дроби стремятся к 0, т.е. имеем неопределенность вида
и числитель, и знаменатель дроби стремятся к 0, т.е. имеем неопределенность вида 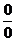 . Для раскрытия неопределенности предварительно избавимся от иррациональности, сделав замену
. Для раскрытия неопределенности предварительно избавимся от иррациональности, сделав замену 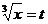 . Тогда
. Тогда 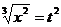 ,
, 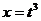 .
.
При 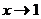
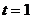 . Теперь
. Теперь 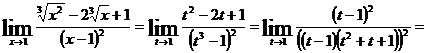
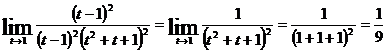
Вопросы для самопроверки:
1. Какая функция называется бесконечно малой?
2. Какова связь между бесконечно малой и бесконечно большой функциями?
3. Сформулируйте основные теоремы о пределах.
4. Дайте определение непрерывной функции в точке и на промежутке (а;в).
Тема 3. Дифференциальное исчисление
Полезно выписать производные основных элементарных функций для случая, когда аргумент этих функций U есть в свою очередь функция от независимой переменной х, т.е. U=U(x):
1. 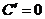 ,
, 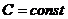 ; 2.
; 2. 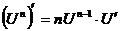 ,
, 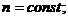
3. 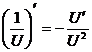 ; 4.
; 4. 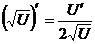 ; 5.
; 5. 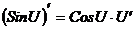 ;
;
6. 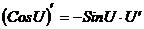 ; 7.
; 7. 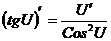 ;
;
8. 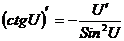 ; 9.
; 9. 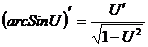 ;
;
10. 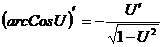 ;
;  11.
11. 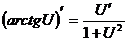 ;
;
12. 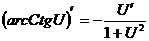 ; 13.
; 13. 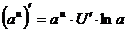 ;
;
14. 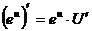 ; 15.
; 15. 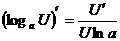 ; 16.
; 16. 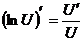 ;
;
Данные производные позволяют дифференцировать всякую сложную функцию, которая представляет собой цепочку основных элементарных функций. Если 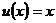 , то
, то 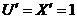 и вышеприведенный перечень упрощается:
и вышеприведенный перечень упрощается:
1. 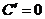 ,
, 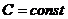 ;
;
2. 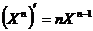 ,
, 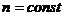 ;
;
3. 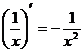 ; и т.д.
; и т.д.
Задача 1. Найти производную функции 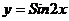 .
.
Решение: 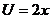
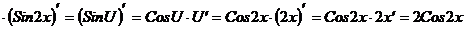
Задача 2. Найти 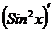 .
.
Решение: 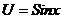 Тогда
Тогда 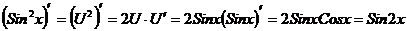 .
.
Если известна производная 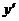 функции
функции 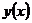 , то дифференциал функции может быть легко вычислен по формуле:
, то дифференциал функции может быть легко вычислен по формуле: 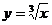 .
.
Решение: Найдем производную 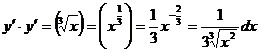 .
.
Вопросы для самопроверки:
1. Дайте определение производной функции. Найдите производную функции 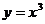 с помощью определения производной.
с помощью определения производной.
2. Геометрический смысл производной функции.
3. Физический смысл первой и второй производной.
4. Сформулируйте правила дифференцирования сложных функций.
5. Чем отличается дифференциал функции от ее приращения?
Тема 4. Приложения дифференциального исчисления
Согласно правилу Лопиталя, если функции 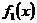 и
и 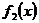 одновременно стремится к 0 или
одновременно стремится к 0 или 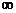 при
при 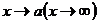 , то
, то 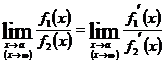 .
.
Если отношение производных функций тоже имеет вид 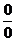 или
или 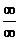 , то можно снова применить правило Лопиталя и так несколько раз до получения результата.
, то можно снова применить правило Лопиталя и так несколько раз до получения результата.
Задача 1. Найти 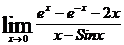 .
.
Решение:
При х, стремящемся к 0, числитель и знаменатель стремятся также к 0, т.е. имеем неопределенность вида 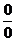 и применимо правило Лопиталя:
и применимо правило Лопиталя:
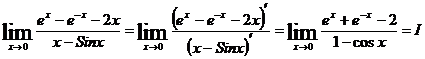
При х, стремящемся к 0, числитель и знаменатель новой дроби стремятся к 0. По правилу Лопиталя:
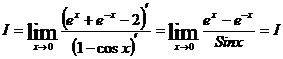
По-прежнему имеем неопределенность вида 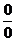 , т.к.
, т.к. 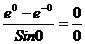
Применяя еще раз правило Лопиталя, получаем:
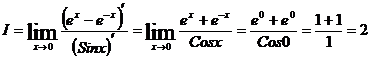
Для отыскания экстремумов и промежутков монотонности функции 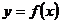 поступаем следующим образом:
поступаем следующим образом:
1. Находим производную 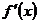 .
.
2. Находим точки, в которых 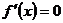 или
или 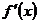 не существует.
не существует.
3. Разбиваем этими точками область определения 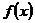 на промежутки.
на промежутки.
4. Методом проб определяем знак 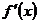 в этих промежутках и находим интервалы монотонности.
в этих промежутках и находим интервалы монотонности.
5. Применяем достаточное условие экстремума. Согласно ему точка, в которой 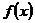 определена, а
определена, а 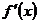 меняет знак с минуса на плюс, есть точка минимума. Точка, в которой
меняет знак с минуса на плюс, есть точка минимума. Точка, в которой 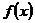 определена, а
определена, а 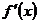 меняет знак с плюса на минус, есть точка максимума.
меняет знак с плюса на минус, есть точка максимума.
Задача 2. Найти интервалы монотонности и точки экстремума функции 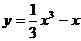 .
.
Решение: 1. 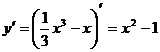 ;
;
2. 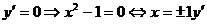 существует для
существует для 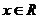 .
.
3. Разбиваем значениями Х= 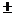 1 числовую ось Х на промежутки:
1 числовую ось Х на промежутки:
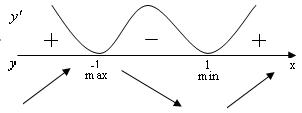
4. 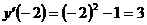 и, следовательно,
и, следовательно, 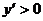 во всем промежутке
во всем промежутке 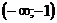 Функция в этом промежутке возрастает.
Функция в этом промежутке возрастает.
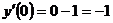 и, следовательно,
и, следовательно, 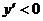 во всем промежутке
во всем промежутке 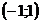 и здесь функция убывает.
и здесь функция убывает.
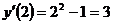 и, следовательно,
и, следовательно, 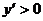 в промежутке
в промежутке 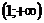 , а функция возрастает.
, а функция возрастает.
5. Из чертежа следует, что 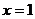 есть точка максимума, а
есть точка максимума, а 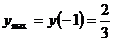
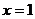 есть точка минимума, а
есть точка минимума, а 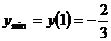 .
.
Вопросы для самопроверки:
1. В чем заключается правило Лопиталя?
2. Каковы признаки возрастания и убывания функции?
3. Сформулируйте достаточные условия экстремума функции.
4. Как находятся интервалы выпуклости и вогнутости и точки перегиба кривой 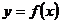 ?
?
Тема 5. Функции нескольких переменных
Основная проблема при изучении этой темы возникает в момент дифференцирования указанных функций. Это связано с тем, что при дифференцировании функции по одной переменной все другие переменные предполагаются постоянными величинами. Например,
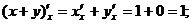
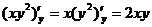
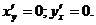
Задача 1. Найти частные производные функции 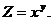
Решение: Найдем производную функции Z по переменной x. В этом случае, при дифференцировании величина y считается постоянной и поэтому: 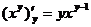
Аналогично найдем производную функции по y, считая величину x постоянной: 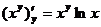
Вопросы для самопроверки:
1. Что называется функцией двух переменных?
2. Дайте определения частных производных.
3. Как находится экстремум функции нескольких переменных?
4. В чем состоит способ наименьших квадратов построения эмпирических формул?
Задачи для самоконтроля
Задание 1. Вычисление пределов
1.а) 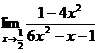 ; б)
; б) 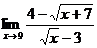 ;
;
в) 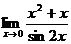 ; г)
; г) 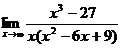 .
.
2. а) 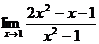 ; б)
; б) 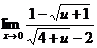 ;
;
в) 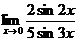 ; г)
; г) 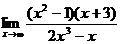 .
.
3. а) 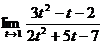 ; б)
; б) 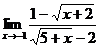 ;
;
в) 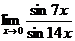 ; г)
; г) 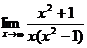 .
.
4. а) 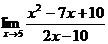 ; б)
; б) 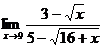 ;
;
в) 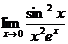 ; г)
; г) 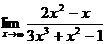 .
.
5. а) 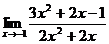 ; б)
; б) 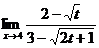 ;
;
в) 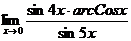 ; г)
; г) 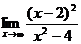 .
.
6. а) 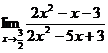 ; б)
; б) 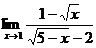 ;
;
в) 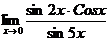 ; г)
; г) 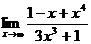 .
.
7. а) 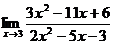 ; б)
; б) 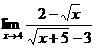 ;
;
в) 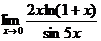 ; г)
; г) 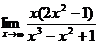 .
.
8. а) 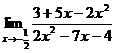 ; б)
; б) 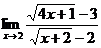 ;
;
в) 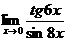 ; г)
; г) 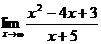 .
.
9. а) 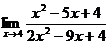 ; б)
; б) 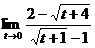 ;
;
в) 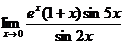 ; г)
; г) 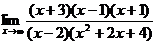 .
.
10. а) 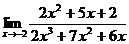 ; б)
; б) 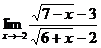 ;
;
в) 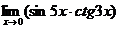 ; г)
; г) 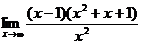 .
.
Задание 2. Дифференциальное исчисление
Найти производную и дифференциал функций:
11. 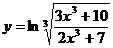 ; 16.
; 16. 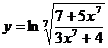 ;
;
12. 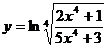 ; 17.
; 17. 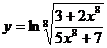 ;
;
13. 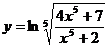 ; 18.
; 18. 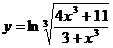 ;
;
14. 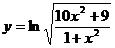 ; 19.
; 19. 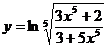 ;
;
15. 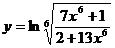 ; 20.
; 20. 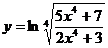 .
.
Найти производную 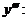
21. 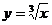 ; 26.
; 26. 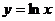 ;
;
22. 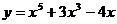 ; 27.
; 27. 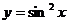 ;
;
23. 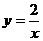 ; 28.
; 28. 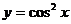 ;
;
24. 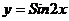 ; 29.
; 29. 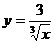 ;
;
25. 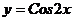 ; 30.
; 30. 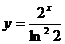 .
.
Найти пределы функций с помощью правила Лопиталя:
31. 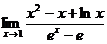 ; 36.
; 36. 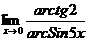 ;
;
32. 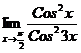 ; 37.
; 37. 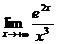 ;
;
33. 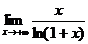 ; 38.
; 38. 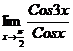 ;
;
34. 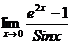 ; 39.
; 39. 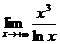 ;
;
35. 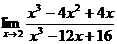 ; 40.
; 40. 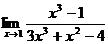 .
.
Исследовать функцию и построить график :
41. 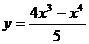 ; 46.
; 46. 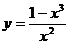 ;
;
42. 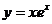 ; 47.
; 47. 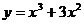 ;
;
43. 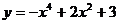 ; 48.
; 48. 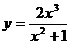 ;
;
44. 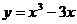 ; 49.
; 49. 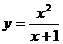 ;
;
45. 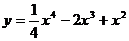 ; 50.
; 50. 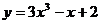 .
.
Задание 4. Функции нескольких переменных.
Найти частные производные функции Z = Z(x,y)
61. Z = 2x3-3xy2+y5;
62. Z = x4+2x2-xy3 ;
63. Z = 5x-2x3y2+2y4;
64. Z = -x2+5xy5-2y3x;
65. Z = x3-3x2y+xy2-y3;
66. Z = 4x-7x4y+3y5;
67. Z = x4+2x2y2+y4;
68. Z = x3+3x2y+3xy2+y3;
69. Z = 6x3-5x2y3+x3y2;
70. Z = x6+2x3y2+y4.
Найти экстремумы функций:
71. Z = x3+8y3+6xy+5;
72. Z = x2+xy+y2-3x-6y;
73. Z = x2+y2+8x-2;
74. Z = y2+yx+x2-6y-9x;
75. Z = x2-xy+y2+9x-6y+20;
76. Z = 3x2-y2+4y+5;
77. Z = x2-4x+y2;
78. Z = x2+xy+2y2-x+y;
79. Z = 3x2-6x-y2+4y+8;
80. Z = x2+xy+x+2y2+2y.
