I. Элементы линейной алгебры и аналитической геометрии.
II.Элементы функционального и комплексного анализа.
Понятие множества.
Задачи для самоконтроля
Задание 1. Вычисление пределов
1.а) 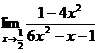 ; б)
; б) 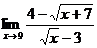 ;
;
в) 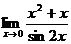 ; г)
; г) 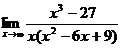 .
.
2. а) 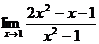 ; б)
; б) 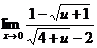 ;
;
в) 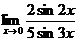 ; г)
; г) 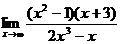 .
.
3. а) 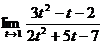 ; б)
; б) 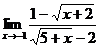 ;
;
в) 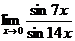 ; г)
; г) 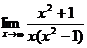 .
.
4. а) 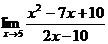 ; б)
; б) 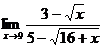 ;
;
в) 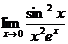 ; г)
; г) 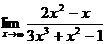 .
.
5. а) 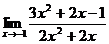 ; б)
; б) 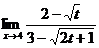 ;
;
в) 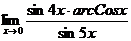 ; г)
; г) 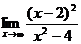 .
.
6. а) 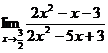 ; б)
; б) 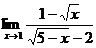 ;
;
в) 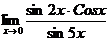 ; г)
; г) 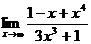 .
.
7. а) 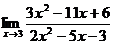 ; б)
; б) 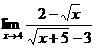 ;
;
в) 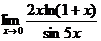 ; г)
; г) 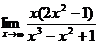 .
.
8. а) 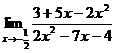 ; б)
; б) 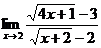 ;
;
в) 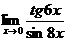 ; г)
; г) 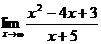 .
.
9. а) 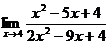 ; б)
; б) 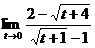 ;
;
в) 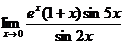 ; г)
; г) 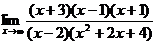 .
.
10. а) 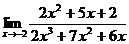 ; б)
; б) 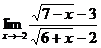 ;
;
в) 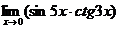 ; г)
; г) 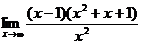 .
.
Задание 2. Дифференциальное исчисление
Найти производную и дифференциал функций:
11. 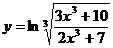 ; 16.
; 16. 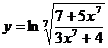 ;
;
12. 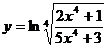 ; 17.
; 17. 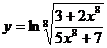 ;
;
13. 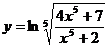 ; 18.
; 18. 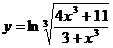 ;
;
14. 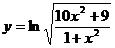 ; 19.
; 19. 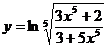 ;
;
15. 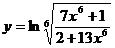 ; 20.
; 20. 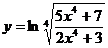 .
.
Найти производную 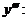
21. 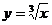 ; 26.
; 26. 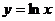 ;
;
22. 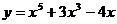 ; 27.
; 27. 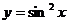 ;
;
23. 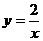 ; 28.
; 28. 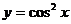 ;
;
24. 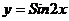 ; 29.
; 29. 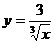 ;
;
25. 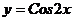 ; 30.
; 30. 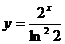 .
.
Найти пределы функций с помощью правила Лопиталя:
31. 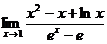 ; 36.
; 36. 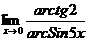 ;
;
32. 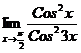 ; 37.
; 37. 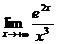 ;
;
33. 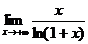 ; 38.
; 38. 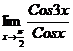 ;
;
34. 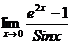 ; 39.
; 39. 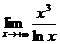 ;
;
35. 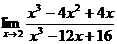 ; 40.
; 40. 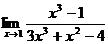 .
.
Исследовать функцию и построить график :
41. 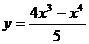 ; 46.
; 46. 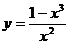 ;
;
42. 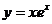 ; 47.
; 47. 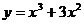 ;
;
43. 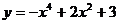 ; 48.
; 48. 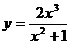 ;
;
44. 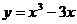 ; 49.
; 49. 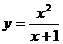 ;
;
45. 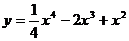 ; 50.
; 50. 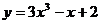 .
.
Задание 4. Функции нескольких переменных.
Найти частные производные функции Z = Z(x,y)
61. Z = 2x3-3xy2+y5;
62. Z = x4+2x2-xy3 ;
63. Z = 5x-2x3y2+2y4;
64. Z = -x2+5xy5-2y3x;
65. Z = x3-3x2y+xy2-y3;
66. Z = 4x-7x4y+3y5;
67. Z = x4+2x2y2+y4;
68. Z = x3+3x2y+3xy2+y3;
69. Z = 6x3-5x2y3+x3y2;
70. Z = x6+2x3y2+y4.
Найти экстремумы функций:
71. Z = x3+8y3+6xy+5;
72. Z = x2+xy+y2-3x-6y;
73. Z = x2+y2+8x-2;
74. Z = y2+yx+x2-6y-9x;
75. Z = x2-xy+y2+9x-6y+20;
76. Z = 3x2-y2+4y+5;
77. Z = x2-4x+y2;
78. Z = x2+xy+2y2-x+y;
79. Z = 3x2-6x-y2+4y+8;
80. Z = x2+xy+x+2y2+2y.
IV. Интегральное исчисление функции одной переменной.
Тема 1. Неопределенный интеграл
[1, гл IX, §9.1 – 9.3],[4, гл VII]
Эффективным способом интегрирования функций является замена переменной. Его целью является получение с помощью новой переменной более простого интеграла.
Задача 1. Найти 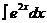
Решение:
Сделаем замену 2x=t. Для нахождения dx через t продифференцируем обе части уравнения:
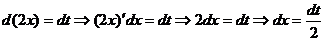 . Теперь
. Теперь 
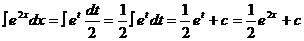 .
.
Задача 2. Найти 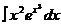 .
.
Решение:1-й способ. Сделаем замену
э 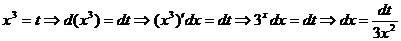
Очевидно, выразить dx только через t рациональным способом не удается. Однако после подстановки полученных выражений для 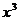 и dx через t исходный интеграл принимает вид:
и dx через t исходный интеграл принимает вид:
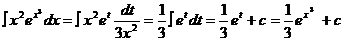 . Можно было поступить по-другому. Нетрудно видеть, что в равенстве
. Можно было поступить по-другому. Нетрудно видеть, что в равенстве 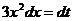 левая часть содержит часть подынтегрального выражения, а именно
левая часть содержит часть подынтегрального выражения, а именно 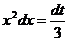 . Поэтому
. Поэтому 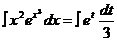 и т.д.
и т.д.
2-й способ. Сделаем другую замену:
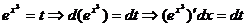
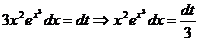 и подынтегральное выражение сразу очень просто выражается через t:
и подынтегральное выражение сразу очень просто выражается через t:
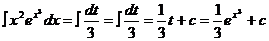 .
.
Вопросы для самопроверки.
1. Дайте определение первообразной.
2. Что называется неопределенным интегралом? Чем он отличается от первообразной?
3. Каковы основные методы интегрирования?
Тема 6. Определенный интеграл
[3, гл IX, § 9.4-9.6, зад и упр. 6-8,15,16],[4, гл IX, § 1-4].
Одним из наиболее распространенных приложений определенного интеграла является решение физически задач. Если точка движется по некоторой кривой со скоростью V(t)≥0, то путь пройденный точкой за время 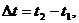 равен:
равен: 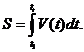
Задача 1. Скорость точки равна 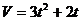 (м/c). Найти путь, который точка преодолела за время t=4c, прошедшее с начала движения.
(м/c). Найти путь, который точка преодолела за время t=4c, прошедшее с начала движения.
Решение: В нашем случае 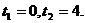
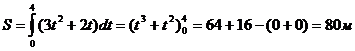 .
.
Вопросы для самопроверки:
1. Что называется определенным интегралом функции f(x) на отрезке [a;b]?
2. Каковы основные свойства определенного интеграла?
3. Каков геометрический смысл определенного интеграла?
4. Каковы особенности нахождения определенного интеграла с помощью подстановки?
5. Какие приложения определенного интеграла Вы знаете?
Задачи для самоконтроля
Найти неопределенные интегралы:
1. а) 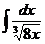 ; б)
; б) 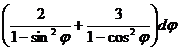 ; в)
; в) 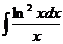 .
.
2. а) 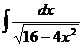 ; б) а)
; б) а) 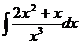 ; в)
; в) 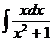 .
.
3. а) 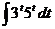 ; б)
; б) 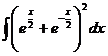 ; в)
; в) 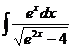 .
.
4. а) 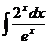 б)
б) 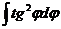 ; в)
; в) 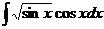 .
.
5. а) 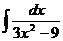 ; б)
; б) 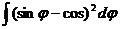 ; в)
; в) 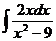 .
.
6. а) 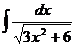 ; б)
; б) 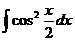 ; в)
; в) 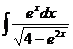 .
.
7. а) 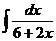 ; б)
; б) 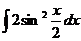 4 в)
4 в) 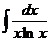 .
.
8. а) 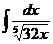 ; б)
; б) 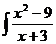 ; в)
; в) 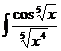 .
.
9. а) 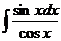 ; б)
; б) 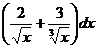 ; в)
; в) 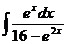 .
.
10. а) 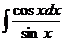 ; б)
; б) 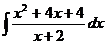 ; в)
; в) 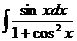 .
.
Вычислить определенные интегралы:
11. 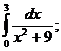 16.
16. 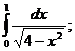
12. 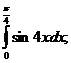 17.
17. 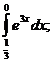
13. 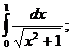 18.
18. 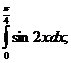
14. 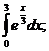 19.
19. 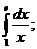
15. 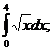 20.
20. 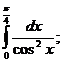
Вычислить площадь фигуры, ограниченной указанными ниже линиями. Сделать чертеж.
21. y = x2, y = x+2;
22. y = x2-3, y = -2x;
23. y = x2-4x, y = -3;
24. y = 2x2-2x-3, y =x2 +3x+3;
25. y = 3x2+2x+1, y =2x2 +3x+3;
26. y = x2, y =4x-3;
27. y = x2-6, y =5x;
28. y = x2+2x, y 3;
29. y = x2-2x-3, y =2x2 –x-5;
30. y = 2x2, y =-x2+3.
Задачи для самоконтроля
Решить уравнения:
1. а) 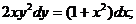 б)
б) 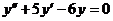 при условиях y(0)=1;
при условиях y(0)=1; 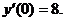
2. а) 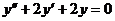 б)
б) 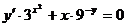 при условии y(0)=1.
при условии y(0)=1.
3. а) 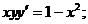 б)
б) 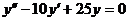 при условиях y(0)=0;
при условиях y(0)=0; 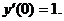
4. а) 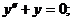 б)
б) 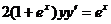 при условии y(0)=0.
при условии y(0)=0.
5. а) 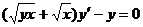 б)
б) 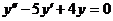 при условиях y(0)=5;
при условиях y(0)=5; 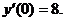
6. а) 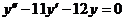 б)
б) 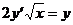 при условии y(4)=1.
при условии y(4)=1.
7. а) 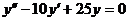 б)
б) 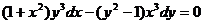 при условии y(1)=-1.
при условии y(1)=-1.
8. а) 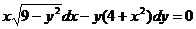 б)
б) 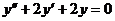 при условиях y(0)=1,
при условиях y(0)=1, 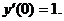
9. а) 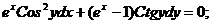 б)
б) 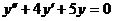 при условиях y(0)=-3,
при условиях y(0)=-3, 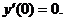
10. а) 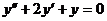 ; б)
; б) 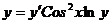 при условиях
при условиях 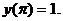
Числовые ряды
Пусть задана бесконечная последовательность чисел 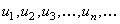 . Выражение
. Выражение
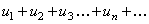
 (1)
(1)
называется числовым рядом. Числа 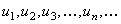 называются членами этого ряда. Член
называются членами этого ряда. Член 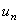 ряда (97), стоящий на
ряда (97), стоящий на 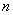 -м месте, считая от начала, называется общим членом этого ряда. Ряд (97) считается заданным, если известен общий член его, выраженный как функция номера
-м месте, считая от начала, называется общим членом этого ряда. Ряд (97) считается заданным, если известен общий член его, выраженный как функция номера 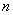 .
.
Выражение (1) удобно обозначать следующим образом: 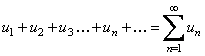 .
.
Сумма конечного числа n первых членов ряда называетсяn-ой частичной суммой ряда.
Рассмотрим частичные суммы: 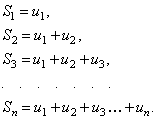
Если существует конечный предел 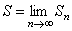 , то его называют суммой ряда (1) и говорят, что ряд (1) сходится.
, то его называют суммой ряда (1) и говорят, что ряд (1) сходится.
Если 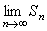 не существует (например
не существует (например 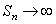 , при
, при 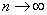 ), то говорят, что ряд (1) расходится и суммы не имеет.
), то говорят, что ряд (1) расходится и суммы не имеет.
Пример 1. Определить сходимость числового ряда
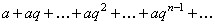 . (2)
. (2)

Решение. Данный числовой ряд – сумма всех членов геометрической прогрессии с первым членом 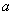 и знаменателем
и знаменателем 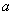
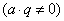 Вычисляя сумму первых
Вычисляя сумму первых 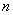 чисел, получаем:
чисел, получаем:
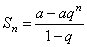 или
или 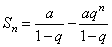 .
.
Переходя к вычислению предела, заметим, что в зависимости от значений 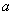 и
и 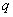 частичная сумма ряда принимает различные значения.
частичная сумма ряда принимает различные значения.
1). Если 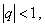 , то
, то 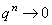 при
при 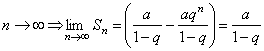 . Значит, в случае
. Значит, в случае 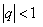 ряд (2) сходится и его сумма
ряд (2) сходится и его сумма 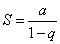 .
.
2). Если 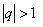 , то
, то 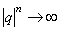 и тогда
и тогда 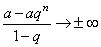 при
при 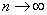 , т.е.
, т.е. 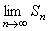 не существует. Таким образом, в случае
не существует. Таким образом, в случае 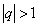 ряд (98) расходится.
ряд (98) расходится.
3) Если 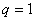 , то ряд (2) имеет вид:
, то ряд (2) имеет вид: 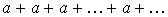 . В этом случае
. В этом случае 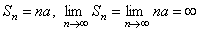 , т.е. ряд расходится.
, т.е. ряд расходится.
Если 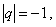 то
то 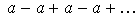 . В этом случае:
. В этом случае: 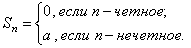
Следовательно, частичная сумма предела не имеет.
Таким образом, сумма членов геометрической прогрессии (с первым членом отличным от нуля) сходится только тогда, когда знаменатель прогрессии по абсолютной величине меньше единицы. ►
Теорема. Если сходится ряд, получившийся из данного ряда (1) отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов.
Теорема. Если ряд (97) сходится и его сумма равная S, то ряд
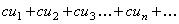 (3)
(3)
где 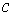 – произвольное действительное число, так же сходится и его сумма равна
– произвольное действительное число, так же сходится и его сумма равна 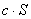 .
.
Теорема.
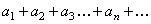 , (4)
, (4)
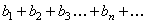 (5)
(5)
сходятся и их суммы, соответственно равны 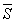 и
и 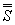 , то ряды
, то ряды
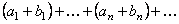 , (6)
, (6)
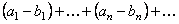 (7)
(7)
также сходятся и их суммы равные соответственно 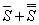 и
и 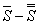 .
.
Теорема. (Необходимый признак сходимости ряда). Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n.
Следствие. Если n-й член ряда не стремится к нулю, то ряд расходится.
Пример 7.1.2. Определить сходимость числового ряда 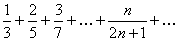 .
.
Решение. Воспользуемся необходимым признаком сходимости ряда. Для данного числового ряда записываем формулу общего члена и вычисляем предел
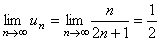 .
.
Так как предел не равен нулю, то исходный ряд расходится. ►
Подчеркнем, что рассмотренный признак является только необходимым, но не является достаточным, то есть из того, что n-й член ряда стремится к нулю, ещё не следует, что ряд сходится – ряд может и расходиться.
Пример 7.1.3. Определить сходимость числового ряда
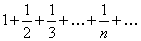 . (8)
. (8)
Решение. Для данного числового ряда записываем формулу общего члена и вычисляем предел 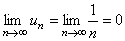 . Необходимый признаквыполнен.Докажем, однако,что исходный ряд расходится. Распишем его подробнее:
. Необходимый признаквыполнен.Докажем, однако,что исходный ряд расходится. Распишем его подробнее:
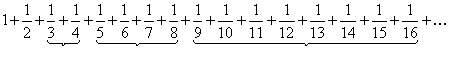 (9)
(9)
и составим вспомогательный ряд:
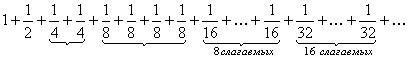 . (10)
. (10)
Ряд (106) строится следующим образом: его первый член равен 1, второй – 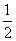 , третий и четвёртый равны
, третий и четвёртый равны 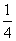 , члены с пятого по восьмой равны
, члены с пятого по восьмой равны 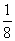 , члены с девятого по 16-й равны
, члены с девятого по 16-й равны 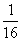 , с 17-го по 32-й –
, с 17-го по 32-й – 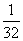 , и т.д.
, и т.д.
Обозначим через Sn(1) сумму первых n членов гармонического ряда (105), а через Sn(2) сумму первых n членов ряда (106). Так как каждый член ряда (105) больше соответствующего члена ряда (106), то для (n > 2) выполнено
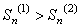 . (11)
. (11)
Подсчитаем частичные суммы ряда (106) для значений n равных степеням двойки: 21, 22, 23, 24, 25 и т.д. Имеем:
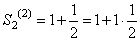 ,
,
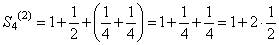 ,
,
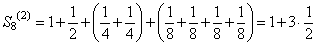 ,
,
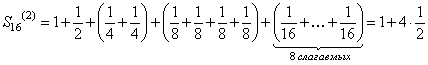 ,
,
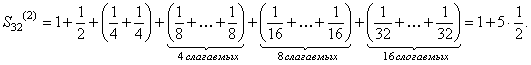
Заметим, что 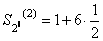 ,
, 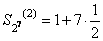 , и т.д. Следовательно
, и т.д. Следовательно 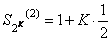 , т.е. частичные суммы Sn(2) при
, т.е. частичные суммы Sn(2) при 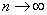 неограниченно увеличиваются или
неограниченно увеличиваются или 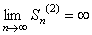 . Но тогда из соотношения (11) следует, что
. Но тогда из соотношения (11) следует, что 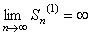 . Таким образом, исходный числовой ряд расходится. Числовой ряд (8) часто называют гармоническим. ►
. Таким образом, исходный числовой ряд расходится. Числовой ряд (8) часто называют гармоническим. ►
Пусть даны два ряда с положительными членами
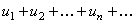 , (12)
, (12)
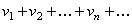 . (13)
. (13)
Для них справедливы следующие утверждения.
Теорема (Первый признак сравнения числовых рядов). Пусть члены ряда (12) не больше соответствующих членов ряда (13), т.е. при n=1, 2, ...
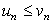 . (14)
. (14)
Тогда, если ряд (109) сходится, то сходится и ряд (12).
Пример 7.1.4. Определить сходимость числового ряда 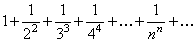 .
.
Решение. Поскольку все слагаемые данного числового ряда положительны, воспользуемся теоремой первым признаком сравнения. Все члены исходного ряда больше соответствующих членов ряда 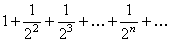 , члены которого образуют геометрическую прогрессию со знаменателем
, члены которого образуют геометрическую прогрессию со знаменателем 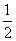 . В примере.1 было показано, что такие числовые ряды (
. В примере.1 было показано, что такие числовые ряды ( 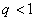 ) сходятся. Более того, сумма этого ряда равна
) сходятся. Более того, сумма этого ряда равна 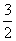 и, следовательно, сумма первоначального ряда не больше чем
и, следовательно, сумма первоначального ряда не больше чем 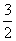 .►
.►
Теорема (Второй признак сравнения числовых рядов). Пусть члены ряда (108) не меньше соответствующих членов ряда (14), т.е. при n=1, 2, ...
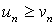 . (15)
. (15)
Тогда, если ряд (12) расходится, то расходится и ряд (13).
Пример 7.1.5. Определить сходимость числового ряда 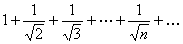 .
.
Решение. Поскольку все слагаемые данного числового ряда положительны, воспользуемся вторым признаком сравнения. Так как 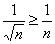 , то члены данного ряда больше соответствующих членов гармонического ряда
, то члены данного ряда больше соответствующих членов гармонического ряда 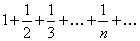 , который расходится (см. пример 3). Поэтому исходный числовой ряд также расходится. ►
, который расходится (см. пример 3). Поэтому исходный числовой ряд также расходится. ►
Теорема (Признак сходимости Даламбера).Пусть дан числовой ряд (97) с положительными членами. Если отношение (n+1)-го члена к n-му члену при 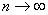 имеет конечный предел, т.е.
имеет конечный предел, т.е.
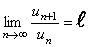 , (16)
, (16)
то 1) при 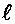 <1 – ряд сходится;
<1 – ряд сходится;
2) при 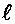 >1 – ряд расходится.
>1 – ряд расходится.
Замечание. Ряд будет расходиться и в том случае, когда 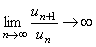 . Это следует из того, что если
. Это следует из того, что если 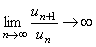 , то, начиная с некоторого номера n=N, будет иметь место неравенство:
, то, начиная с некоторого номера n=N, будет иметь место неравенство: 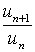 >1. Следовательно,
>1. Следовательно, 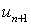 >
> 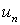 .
.
Пример 7.1.6. Исследовать сходимость ряда 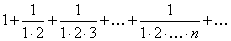
Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим отношение 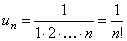 ,
, 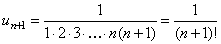 ,
, 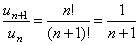 . Вычисляя предел, получим
. Вычисляя предел, получим
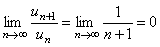 <1.
<1.
Таким образом, исходный ряд сходится. ►
Пример 7.1.7. Исследовать сходимость ряда 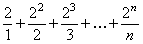 .
.
Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим отношение 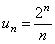 ,
, 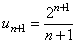 ,
, 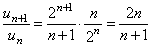 . Вычисляя предел, получим
. Вычисляя предел, получим
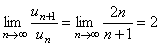 > 1.
> 1.
Таким образом, исходный ряд расходится. ►
Признак Даламбера дает ответ на вопрос о том сходится ли данный положительный ряд в случае, когда 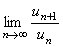 существует и отличен от 1. Если же этот предел не существует или
существует и отличен от 1. Если же этот предел не существует или 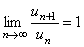 , то признак Даламбера не дает возможности установить, сходится ряд или расходится, так как в этом случае ряд может оказаться или сходящимся, или расходящимся. Для решения вопроса о сходимости надо применить какой-либо другой признак.
, то признак Даламбера не дает возможности установить, сходится ряд или расходится, так как в этом случае ряд может оказаться или сходящимся, или расходящимся. Для решения вопроса о сходимости надо применить какой-либо другой признак.
Если 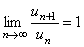 , но отношение
, но отношение 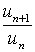 для всех номеров n, начиная с некоторого больше 1, то ряд расходится. Это следует из того, что если
для всех номеров n, начиная с некоторого больше 1, то ряд расходится. Это следует из того, что если 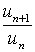 >1, то
>1, то 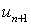 >
> 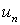 и общий член ряда не стремится к 0 при n®¥.
и общий член ряда не стремится к 0 при n®¥.
Пример 7.1.8. Исследовать сходимость ряда 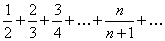 .
.
Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим предел отношения
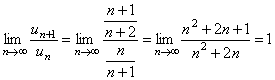 .
.
В данном случае ряд расходится, так как 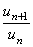 >1 для всех n. Действительно,
>1 для всех n. Действительно,
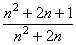 >1 Û
>1 Û 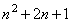 >
> 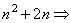 1>0. ►
1>0. ►
Пример 7.1.9. Определить сходимость числового ряда 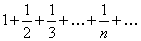 .
.
Решение. Применяя признак сходимости Даламбера к гармоническому ряду, получаем 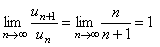 . Признак Даламбера в данном случае не дает ответа на вопрос о сходимости, но в примере 7.1.3 была установлена расходимость данного числового ряда. ►
. Признак Даламбера в данном случае не дает ответа на вопрос о сходимости, но в примере 7.1.3 была установлена расходимость данного числового ряда. ►
Пример 7.1.10. Исследовать сходимость ряда 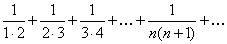 .
.
Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим предел отношения
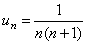 ,
, 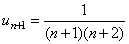 ,
, 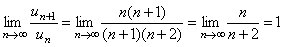 .
.
На основании признака Даламбера сходимость установить нельзя. Однако, так как 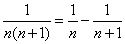 , то можно преобразовать данный ряд
, то можно преобразовать данный ряд
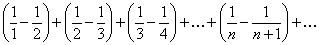
Вычисляя частичные суммы 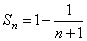 и предел, получаем
и предел, получаем
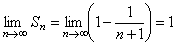 .
.
Таким образом, исходный ряд сходится. ►
Теорема (Признак Коши). Если для ряда с положительными членами (97) величина 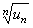 имеет конечный предел
имеет конечный предел 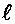 при
при 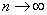 , т.е.
, т.е.
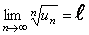 ,
,
то 1) при 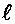 < 1 – ряд сходится;
< 1 – ряд сходится;
 2) при 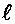 > 1 – ряд расходится.
> 1 – ряд расходится.
Замечание. Как и в признаке Даламбера, случай 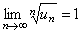 , требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся. Так для гармонического ряда имеем:
, требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся. Так для гармонического ряда имеем: 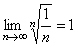 , но он расходится. Рассмотрим другой числовой ряд
, но он расходится. Рассмотрим другой числовой ряд 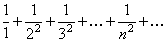 . Для него так же имеет место равенство
. Для него так же имеет место равенство 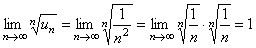 , но он сходится по первому признаку сходимости. Заметим, что если отбросить первый член, то члены оставшегося ряда будут меньше соответствующих членов ряда
, но он сходится по первому признаку сходимости. Заметим, что если отбросить первый член, то члены оставшегося ряда будут меньше соответствующих членов ряда 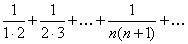 , который сходится (см. пример 7.1.10).
, который сходится (см. пример 7.1.10).
Пример 7.1.11. Исследовать сходимость ряда 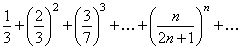
Решение. Воспользуемся признаком сходимости Коши. Определим формулу общего члена числового ряда и вычислим предел 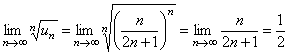 .
.
Так как предел конечен и меньше единицы, то по признаку Коши исходный числовой ряд сходится. ►
Приведем без доказательства признак сходимости числовых рядов с положительными членами, который удобно использовать, когда признаки Даламбера и Коши не дают ответа на вопрос о сходимости ряда.
Теорема (Интегральный признак сходимости).Пусть дан ряд 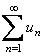 , члены которого положительны и не возрастают, т.е.
, члены которого положительны и не возрастают, т.е. 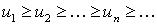 , а функция
, а функция 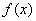 , определена при
, определена при 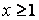 , непрерывная и не возрастающая и
, непрерывная и не возрастающая и 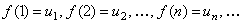 . Тогда для сходимости ряда
. Тогда для сходимости ряда 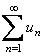 необходимо и достаточно, чтобы сходился несобственный интеграл
необходимо и достаточно, чтобы сходился несобственный интеграл 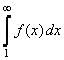 .
.
Пример 7.1.12. Исследовать сходимость обобщенного гармонического ряда 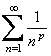 .
.
Решение. Пусть 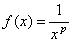 . Функция
. Функция 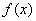 при
при 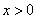 (а значит и при
(а значит и при 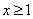 ) положительна и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла
) положительна и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла 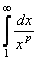 . Имеем
. Имеем 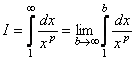 .
.
Если 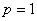 , то
, то 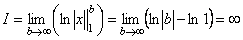 .
.
Если 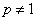 , то
, то 
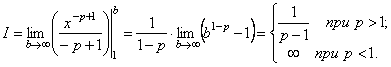
Итак, данный обобщенный гармонический ряд сходится при 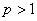 и расходится при
и расходится при 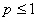 . ►
. ►
Знакочередующимся рядом называется ряд
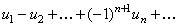 , (17)
, (17)
где 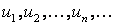 , – положительные числа.
, – положительные числа.
Теорема (Признак Лейбница). Если в знакочередующемся ряде (17) члены таковы, что
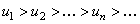 (18)
(18)
и
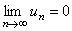 (19)
(19)
то ряд (17) сходится, его сумма положительна и не превосходит первого члена.
Замечание. Теорема Лейбница справедлива, если неравенства выполняются, начиная с некоторого номера N.
Теорема Лейбница иллюстрируется геометрически следующим образом. На числовой прямой будем откладывать (рис. 21)частичные суммы:
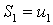 ,
, 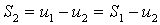 ,
, 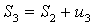 ,
, 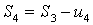 , …
, …
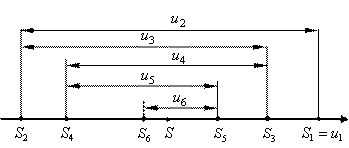
Рис. 21. Геометрический смысл теоремы Лейбница
Тогда точки, соответствующие частичным суммам будут приближаться к некоторой точке S. При этом точки, соответствующие чётным суммам располагаются слева от S, а нечетным суммам – справа от S.
Пример 7.1.13. Исследовать сходимость ряда 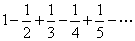 .
.
Решение. Поскольку данный ряд является знакочередующимся, воспользуемся признаком сходимости Лейбница. Определим формулу общего члена числового ряда и проверим условия теоремы. Имеем:
1) 1 > 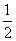 >
> 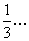 ;
;
2) 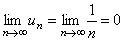 .
.
Так как оба условия выполнены, то исходный ряд сходится по признаку Лейбница. ►
Пример 7.1.14. Исследовать сходимость ряда 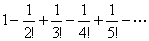
Решение. Поскольку данный ряд является знакочередующимся, воспользуемся признаком Лейбница. Определим формулу общего члена числового ряда и проверим условия теоремы. Имеем:
3) 1 > 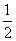 >
> 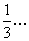 ;
;
4) 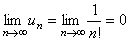 .
.
Так как оба условия выполнены, то исходный ряд сходится по признаку Лейбница. ►
Ряд называется знакопеременным, если среди его членов имеются как положительные так и отрицательные.
Знакочередующиеся ряды являются частным случаем знакопеременных рядов.
Теорема. Если знакопеременный ряд
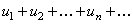 (20)
(20)
таков, что ряд, составленный из абсолютных величин его членов
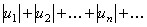 (21)
(21)
сходится, то, и данный знакопеременный ряд также сходится.
Пример 7.1.15. Исследовать сходимость ряда
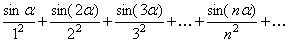 (22)
(22)
где a – любое число.
Решение. Наряду с данным рядом, рассмотрим два следующих ряда:
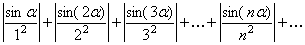 , (23)
, (23)
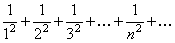 (24)
(24)
Ряд (24) сходится (см. замечание к теореме Коши). Так как члены ряда (23) не больше соответствующих членов ряда (24), т.е.
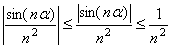 ,
,
то по первому признаку сравнения ряд (23) сходится. Следовательно, по теореме ряд (22) так же сходится. ►
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд называется условно сходящимся.
Пример 7.1.16. Исследовать сходимость ряда 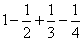 .
.
Решение. Данныйзнакопеременный ряд является условно сходящимся, так как ряд, составленный из абсолютных величин его членов, есть гармонический ряд 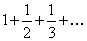 , который расходится. Сам же ряд сходится (см. пример 7.1.13) по признаку Лейбница. ►
, который расходится. Сам же ряд сходится (см. пример 7.1.13) по признаку Лейбница. ►
Пример 7.1.17. Исследовать сходимость ряда 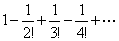 .
.
Решение. Данный знакопеременный ряд абсолютно сходящийся, так как ряд, составленный из абсолютных величин его членов
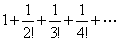
сходится (см. пример 7.1.6). ►
Теорема. (Погрешности при вычислении сумм сходящегося знакопеременного ряда). Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
Теорема. Если ряд сходится условно, то какое бы мы не задали число А, можно так переставить его члены, чтобы его сумма оказалась в точности равной А. Более того, можно так переставить члены условно сходящегося ряда, чтобы ряд, полученный после перестановки, оказался расходящимся.
