Выбор оптимального портфеля ценных бумаг
ВЫБОР ОПТИМАЛЬНОГО ПОРТФЕЛЯ ЦЕННЫХ БУМАГ
Пусть рынок ценных бумаг состоит из n активов
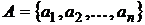 ,
,
с вектором доходностей
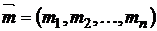
и ковариационной матрицей
 .
.
Тогда портфель 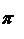 с представляющим его вектором
с представляющим его вектором 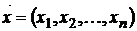 и условием
и условием 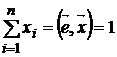 имеет оценку доходности
имеет оценку доходности
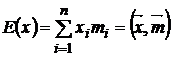 ,
,
и риска
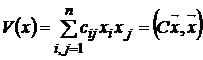 .
.
ВЫБОР ПОРТФЕЛЯ С МИНИМАЛЬНЫМ РИСКОМ
Найдем портфель 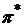 с наименьшим риском, то есть решим оптимизационную задачу:
с наименьшим риском, то есть решим оптимизационную задачу:
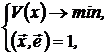 (1)
(1)
в модели Блека.
Для решения этой задачи применим метод множителей Лагранжа. С этой целью составим функцию Лагранжа:
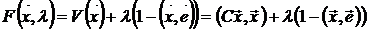 ,
,
и приравняем частные производные первого порядка по 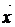 и
и 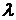 к нулю:
к нулю:
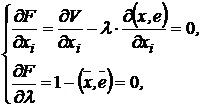 (2)
(2)
или в матричной форме:
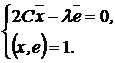 (2’)
(2’)
Если матрица С невырожденная, то из первого уравнения системы (2’) получим:
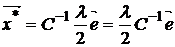 .
.
Подставив это выражение во второе уравнение системы:
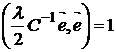 ,
,
получим оптимальное значение множителя Лагранжа:
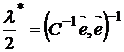 . (3)
. (3)
Следовательно, портфель с минимальным риском задается вектором
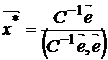 , (4)
, (4)
с наименьшим значением риска:
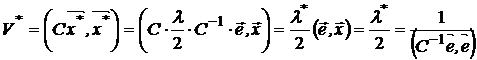 , (5)
, (5)
и соответствующей доходностью:
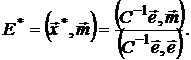 (6)
(6)
Например, при 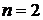 получаем:
получаем:
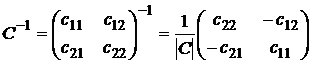 ,
,
где 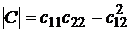 . Тогда
. Тогда
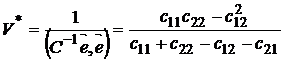 .
.
или
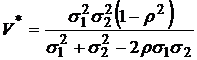 .
.
Отметим также, что минимизация дисперсии может быть оправдана только в том случае, если 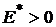 , а это выполняется, если (см. (6)):
, а это выполняется, если (см. (6)):
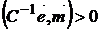 .
.
Если речь идет о модели Марковица, то добавляется условие неотрицательности 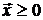 . Наличие такого ограничения в виде неравенства существенно усложняет решение задачи в отличие от модели Блека. В этом случае поступают следующим образом: сначала решают задачу минимизации риска без условия неотрицательности
. Наличие такого ограничения в виде неравенства существенно усложняет решение задачи в отличие от модели Блека. В этом случае поступают следующим образом: сначала решают задачу минимизации риска без условия неотрицательности 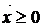 (как в модели Блека); и если некоторые
(как в модели Блека); и если некоторые 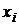 окажутся неположительными, то соответствующие активы исключаются из портфеля и задача решается заново.
окажутся неположительными, то соответствующие активы исключаются из портфеля и задача решается заново.
№ 7.Пусть рынок из трех активов имеет параметры:
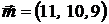 ,
, 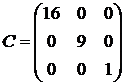
Найти портфель минимальный по риску.
Решение. Составим функцию Лагранжа:
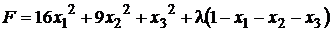 .
.
Вычислим частные производные первого порядка и приравняем их к нулю:
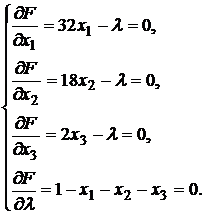
Решив эту систему, получаем оптимальные значения:
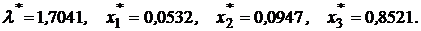
Доходность и риск искомого портфеля будут соответственно равны:
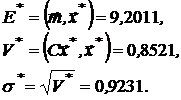
ВЫБОР ПОРТФЕЛЯ МАКСИМАЛЬНОЙ ПОЛЕЗНОСТИ
Выбор оптимального портфеля
Задача максимизации полезности 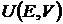 или
или 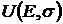 формулируется следующим образом:
формулируется следующим образом:
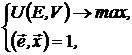 (22)
(22)
для модели Блека, и добавлением неравенства 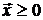 для модели Марковица.
для модели Марковица.
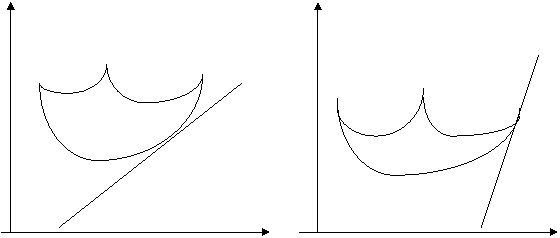
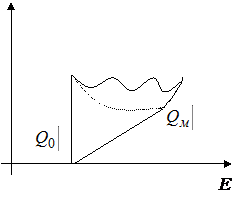
Геометрически решение такой задачи для модели Блека можно представить следующим образом ( 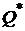 - оптимальный портфель):
- оптимальный портфель):
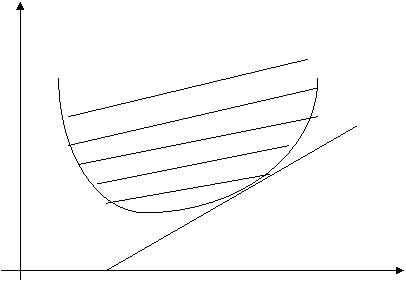
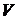
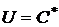
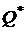
0 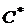
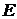
Рис.5.
То есть оптимальная линия уровня 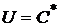 является касательной к эффективной границе критериального множества.
является касательной к эффективной границе критериального множества.
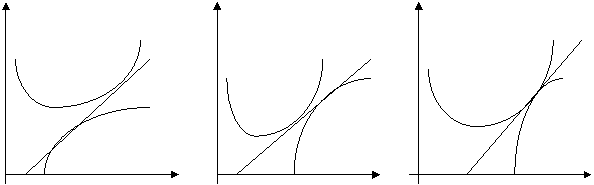
Для модели Марковица возможны два варианта:
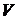
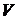
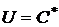
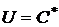
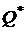
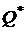
0 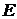 0
0 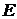
Рис.6.
Во втором случае оптимальная линия уровня 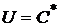 не является касательной к эффективной границе, а имеет с ней общую верхнюю (угловую) точку
не является касательной к эффективной границе, а имеет с ней общую верхнюю (угловую) точку 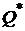 .
.
Найдем аналитическое решение задачи (22) методом множителей Лагранжа, для чего составим функцию:
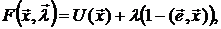
или
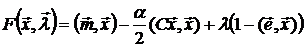 . (23)
. (23)
Вычислим ее частные производные первого порядка и приравняем их к нулю:
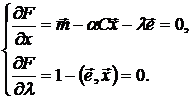
Выразим 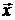 из первого уравнения этой системы:
из первого уравнения этой системы:
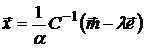
и подставим во второе уравнение
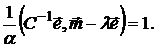
Откуда получаем
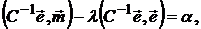
или
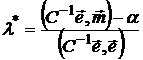 -
-
оптимальное значение множителя Лагранжа.
Следовательно, оптимальный (с точки зрения полезности ) портфель будет иметь вид
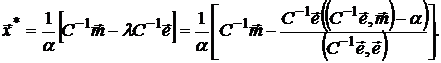 (24)
(24)
Откуда легко вычислить как оптимальное значение полезности 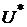 , так и оптимальные характеристики портфеля
, так и оптимальные характеристики портфеля 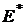 и
и 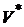 .
.
Если в (24) некоторые 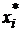 будут отрицательными, то для модели Марковица поступаем так же, как и в предыдущих параграфах.
будут отрицательными, то для модели Марковица поступаем так же, как и в предыдущих параграфах.
№ 12. В условиях № 7 найти портфель максимальной полезности при 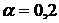 .
.
Решение. Составим функцию Лагранжа
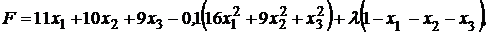
и получим систему уравнений:
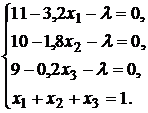
Выразив из первых трех уравнений
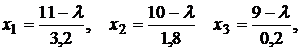
и подставив в четвертое уравнение
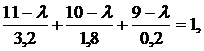
получим
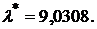
Следовательно, оптимальный портфель будет иметь структуру:
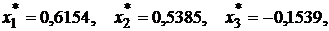
с доходностью
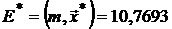 ,
,
риском
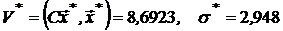 ,
,
и полезностью
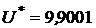 .
.
Так как 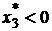 , то оптимальное решение найдено для модели Блэка. Найдем оптимальное решение по Марковицу. Для этого примем
, то оптимальное решение найдено для модели Блэка. Найдем оптимальное решение по Марковицу. Для этого примем 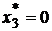 и решим задачу снова, с функцией Лагранжа:
и решим задачу снова, с функцией Лагранжа:
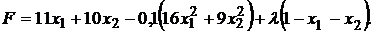 .
.
Тогда
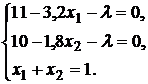
Решив эту систему, получим портфель, оптимальный по Марковицу:
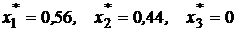 .
.
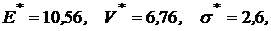
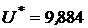 .
.
Если портфель содержит безрисковый актив 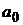 , то для построения оптимального портфеля строим следующую функцию Лагранжа
, то для построения оптимального портфеля строим следующую функцию Лагранжа
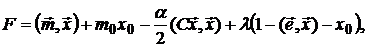
что приводит к системе уравнений
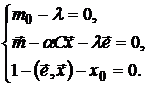 (25)
(25)
Подставив 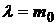 во второе уравнение, получаем следующую структуру оптимального портфеля
во второе уравнение, получаем следующую структуру оптимального портфеля
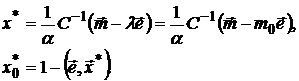
№ 13. Решите № 12 при условии, что актив  - безрисковый.
- безрисковый.
Решение. Составив функцию Лагранжа:
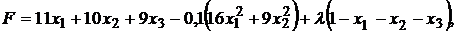
получаем систему уравнений
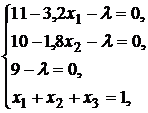
решение которой имеет вид:
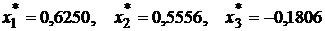 ,
,
с доходностью
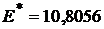 ,
,
риском
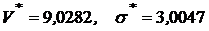 ,
,
и полезностью
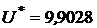 .
.
Так как 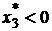 , то это решение - оптимальное в модели Блека. Найдем решение оптимальное по Марковицу, для чего примем
, то это решение - оптимальное в модели Блека. Найдем решение оптимальное по Марковицу, для чего примем 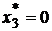 . Тогда
. Тогда
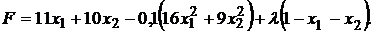
и
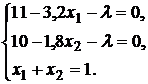
Решив эту систему, получаем:
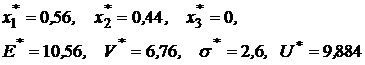
Критериальное множество
Пусть инвестор имеет возможность сформировать портфель, содержащий кроме чисто рисковых активов  и так называемый безрисковый актив
и так называемый безрисковый актив 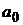 , с параметрами
, с параметрами 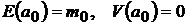 . Тогда ковариационная матрица
. Тогда ковариационная матрица 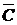 будет вырожденной, имеющей нулевые первую строку и первый столбец.
будет вырожденной, имеющей нулевые первую строку и первый столбец.
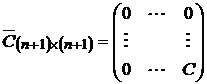 ,
,
где 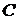 – невырожденная ковариационная матрица для рисковых активов, а вектор доходностей –
– невырожденная ковариационная матрица для рисковых активов, а вектор доходностей – 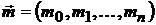 .
.
Представим портфель 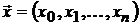 в виде суммы двух портфелей (безрискового
в виде суммы двух портфелей (безрискового 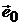 и чисто рискового
и чисто рискового 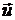 ):
):
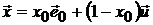 ,
,
где
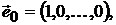
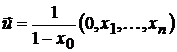 .
.
Построим на плоскости 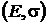 критериальное множество для рисковых портфелей
критериальное множество для рисковых портфелей 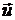 и оценку
и оценку 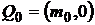 безрискового портфеля
безрискового портфеля 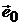 .
.
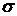

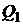
0 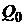
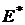
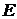
Рис.7.
Оценка 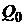 лежит левее
лежит левее 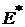 , то есть
, то есть 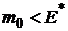 , что естественно, так как в безрисковый актив должен иметь доходность ниже, чем «наилучший по риску» портфель, состоящий из рисковых активов.
, что естественно, так как в безрисковый актив должен иметь доходность ниже, чем «наилучший по риску» портфель, состоящий из рисковых активов.
Составим следующую линейную комбинацию рискового и безрискового портфелей:
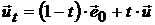 , (26)
, (26)
и вычислим его характеристики:
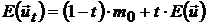 ,
,
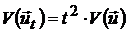 ,
,
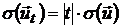 .
.
Таким образом, риск портфеля, состоящего из безрискового актива 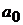 и «рискового актива»
и «рискового актива» 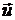 , равен произведению риска «рискового актива»
, равен произведению риска «рискового актива» 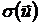 на его удельный вес
на его удельный вес 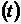 в портфеле. Изменяя удельный вес
в портфеле. Изменяя удельный вес  актива
актива 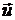 , инвестор может построить портфель с различными характеристиками риска и доходности, все они располагаются на отрезках вида
, инвестор может построить портфель с различными характеристиками риска и доходности, все они располагаются на отрезках вида 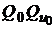 и их риск пропорционален удельному весу
и их риск пропорционален удельному весу 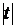 рискованного актива. Такой портфель можно рассматривать как покупку инвестором рискового актива в сочетании с предоставлением кредита (покупка актива
рискованного актива. Такой портфель можно рассматривать как покупку инвестором рискового актива в сочетании с предоставлением кредита (покупка актива 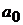 ), так как приобретение актива без риска есть не что иное, как кредитование эмитента. Поэтому портфели на отрезке
), так как приобретение актива без риска есть не что иное, как кредитование эмитента. Поэтому портфели на отрезке 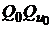 , где
, где 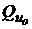 лежит на минимальной границе рисковых портфелей, например,
лежит на минимальной границе рисковых портфелей, например, 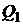 называют кредитными.
называют кредитными.
Инвестор может построить свою стратегию не только на основе предоставления кредита, но и заимствуя средства под более низкий процент, чем ожидаемая доходность рискового актива 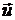 , с целью приобретения на них активов
, с целью приобретения на них активов 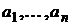 , для получения дополнительного дохода. В этом случае
, для получения дополнительного дохода. В этом случае 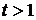 , и инвестор может получить более высокий доход, чем
, и инвестор может получить более высокий доход, чем 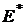 , но с более высоким риском, чем
, но с более высоким риском, чем 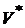 , например, это портфель
, например, это портфель 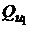 . Поскольку для формирования такого портфеля инвестор занимает средства, то его еще называют заемным портфелем. Это портфели, оценки которых лежат, например, на луче
. Поскольку для формирования такого портфеля инвестор занимает средства, то его еще называют заемным портфелем. Это портфели, оценки которых лежат, например, на луче 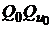 «выше», чем
«выше», чем  .
.
Таким образом, на плоскости 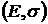 оценки портфелей (26) будут лежать на лучах, соединяющих оценку
оценки портфелей (26) будут лежать на лучах, соединяющих оценку 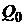 безрискового портфеля
безрискового портфеля 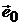 с оценкой
с оценкой 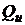 рискового портфеля
рискового портфеля 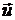 . Меняя
. Меняя 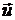 , будем получать различные лучи, совокупность которых и составит критериальное множество для класса всех портфелей вида (26):
, будем получать различные лучи, совокупность которых и составит критериальное множество для класса всех портфелей вида (26):
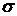


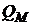
 | |||
 |
 0
0 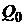
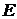
Рис.8.
Это множество представляет собой часть плоскости, ограниченной парой крайних лучей, выходящих из точки 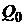 . Правый луч будет касательным к гиперболе (минимальной границе критериального множества портфеля
. Правый луч будет касательным к гиперболе (минимальной границе критериального множества портфеля 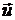 ), а левый луч будет параллелен левой асимптоте этой гиперболы. Оценка
), а левый луч будет параллелен левой асимптоте этой гиперболы. Оценка 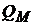 - это точка касания граничного луча с гиперболой.
- это точка касания граничного луча с гиперболой.
Для модели Марковица случай с безрисковым активом 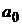 рассматривается также, как и в модели Блека. И критериальное множество на плоскости
рассматривается также, как и в модели Блека. И критериальное множество на плоскости 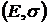 будет иметь следующий вид.
будет иметь следующий вид.
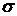
|
Рис.9.
Теорема отделения
Вывод, сформулированный в §5.2, о стратегии инвестора по формированию портфеля, включающего в себя процедуры кредитования и заимствования состоит в том, что в качестве рисковой части портфеля он обязательно должен приобретать портфель 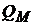 . В этом случае инвестор может получить портфель с наилучшими параметрами риска и доходности.
. В этом случае инвестор может получить портфель с наилучшими параметрами риска и доходности.
Данное положение получило название теоремы отделения, которое гласит, что независимо от индивидуальных предпочтений в отношении формируемого портфеля, инвестор обязательно должен включать 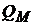 в формируемый им портфель. Другими словами, выбор портфеля
в формируемый им портфель. Другими словами, выбор портфеля 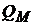 не зависит от выбора ожидаемой доходности и риска портфеля, так как в этом случае инвестор, как мы видели выше, всегда имеет возможность сформировать портфель с лучшими параметрами (
не зависит от выбора ожидаемой доходности и риска портфеля, так как в этом случае инвестор, как мы видели выше, всегда имеет возможность сформировать портфель с лучшими параметрами ( 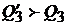 в случае заемного портфеля, или
в случае заемного портфеля, или 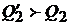 – в случае кредитного портфеля).
– в случае кредитного портфеля).
Следовательно, при формировании портфеля инвестор должен только решить: в какой степени финансировать свою стратегию за счет кредитования или заимствования, так как рисковый портфель – это портфель 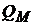 , а конкретный уровень доходности и риска зависит только от масштабов заимствования и кредитования.
, а конкретный уровень доходности и риска зависит только от масштабов заимствования и кредитования.
Рыночный портфель
Рыночный портфель – это портфель, в который входят все существующие финансовые инструменты в пропорции, равной их удельному весу в совокупной стоимости финансовых активов на рынке.
Понятие рыночного портфеля вводится для описания поведения инвестора на рынке на основе моделей, которые имеют некоторые ограничения по сравнению с реальными условиями. То есть предполагается, что поведение всех участников рынка соответствует одной и той же модели, то есть они знают все параметры рынка  и принимают на ее основе наилучшие решения, основываясь на критериях доходности и риска.
и принимают на ее основе наилучшие решения, основываясь на критериях доходности и риска.
В зависимости от соотношения спроса и предложения цены на активы уменьшаются (при избыточности предложений) или растут (при дефиците). С учетом этих ценовых изменений корректируются и параметры рынка, а следовательно, и спрос на ценные бумаги. Этот процесс самоорганизуется таким образом, что по всем видам финансовых активов предложение и спрос выравниваются. В результате рисковый портфель инвестора начинает копировать структуру рыночного портфеля.
В реальной жизни практически невозможно сформировать рыночный портфель, так как он должен включать в себя все финансовые активы, среди которых много кратковременных (за год образуются и погибают тысячи корпораций, выпускающих свои ценные бумаги), есть малорисковые, относительно которых не ясно, признавать ли их безрисковым и т.д.
Поэтому на практике отбирают наиболее важные для рынка ценные бумаги с длительной историей. Обработка этих активов по специальным правилам позволяет получать разнообразные индексы, каждый из которых может характеризовать эффективность рынка. И в качестве рыночных рассматривают портфели, которые образованы на основе таких индексов, как например: индекс РТС, индекс Доу Джонса (DJIA), Staandard&Poor’s 500 index (S&P500) и так далее.
Кроме того, возможны и отклонения от построенного рыночного портфеля в виду нарушения условий «идеальности» существования рынка. Это – несимметричность информации, нестационарность рынка, воздействие внешних факторов (кризисы на фондовых рынках) и т.д. Поэтому очень важным является вопрос о прогнозировании структуры рыночного портфеля.
Таким образом, в качестве рискового портфеля 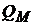 инвестор выбирает рыночный портфель, и формирование конкретного портфеля производится в зависимости от предпочтений инвестора.
инвестор выбирает рыночный портфель, и формирование конкретного портфеля производится в зависимости от предпочтений инвестора.
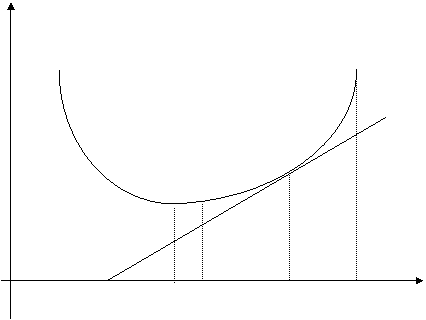
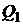
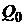
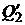
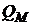
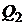
0 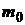
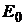
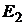
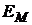
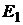
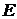
Рис.14.
Если требуемый уровень доходности портфеля равен 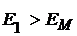 , инвестор формирует либо заемный портфель
, инвестор формирует либо заемный портфель 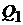 , либо чисто рисковый портфель
, либо чисто рисковый портфель 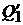 . Если уровень доходности равен
. Если уровень доходности равен 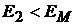 , то он формирует либо кредитный портфель
, то он формирует либо кредитный портфель 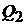 , либо чисто рисковый портфель
, либо чисто рисковый портфель 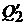 .
.
Если предпочтения инвестора оцениваются функцией полезности 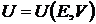 , то инвестор формирует либо заемный
, то инвестор формирует либо заемный 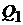 , либо кредитный
, либо кредитный 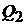 , либо рисковый
, либо рисковый 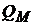 портфели.
портфели.
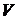
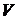
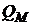
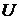
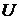
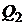
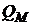
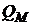
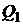
0 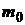
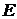 0
0 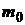
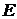 0
0 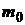
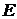
Рис.15.
И ставки по займам
Выше предполагалось, что при формировании заемного портфеля инвестор мог получить заем под процент 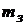 , равный ставке доходности безрискового актива. На практике же между этими ставками наблюдается существенная разница, причем
, равный ставке доходности безрискового актива. На практике же между этими ставками наблюдается существенная разница, причем 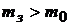 .
.
Тогда эффективная граница примет вид 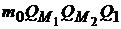 :
:
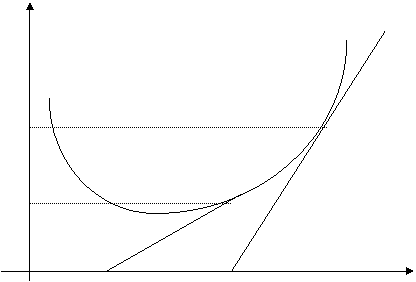
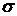
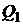
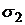
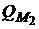
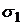
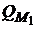
0 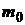
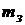
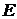
Рис.16.
Здесь 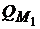 и
и 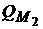 – точки касания эффективной границы рисковых портфелей с лучами
– точки касания эффективной границы рисковых портфелей с лучами 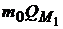 и
и 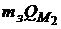 .
.
Если инвестор желает ограничить свой риск в пределах 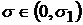 , то он должен приобрести актив без риска и рисковый портфель
, то он должен приобрести актив без риска и рисковый портфель 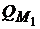 , что позволит получить ему любой кредитный портфель на отрезке
, что позволит получить ему любой кредитный портфель на отрезке 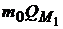 .
.
Если допустимый риск инвестора лежит в пределах 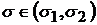 , то он формирует портфель на дуге
, то он формирует портфель на дуге 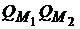 , то есть инвестор не прибегает ни к заимствованию, ни к кредитованию, и любой портфель на
, то есть инвестор не прибегает ни к заимствованию, ни к кредитованию, и любой портфель на 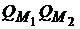 будет для него рыночным. Если инвестор согласен пойти на риск больший, чем
будет для него рыночным. Если инвестор согласен пойти на риск больший, чем 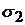 , то он должен ограничиться портфелями на луче
, то он должен ограничиться портфелями на луче 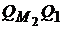 , то есть сформировать заемный портфель.
, то есть сформировать заемный портфель.
ВЫБОР ОПТИМАЛЬНОГО ПОРТФЕЛЯ ЦЕННЫХ БУМАГ
Пусть рынок ценных бумаг состоит из n активов
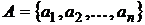 ,
,
с вектором доходностей
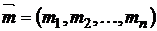
и ковариационной матрицей
 .
.
Тогда портфель 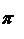 с представляющим его вектором
с представляющим его вектором 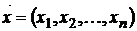 и условием
и условием 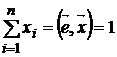 имеет оценку доходности
имеет оценку доходности
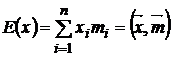 ,
,
и риска
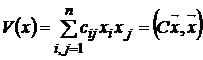 .
.