Связь понятия выпуклости функции с поведением ее производной
Теорема. Пусть функция  определена на
определена на 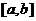 и в каждой точке этого промежутка существует
и в каждой точке этого промежутка существует 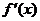 . Тогда для того чтобы
. Тогда для того чтобы  была выпуклой необходимо и достаточно, чтобы ее производная была монотонно возрастающей функцией.
была выпуклой необходимо и достаточно, чтобы ее производная была монотонно возрастающей функцией.
Доказательство этой довольно громоздкой теоремы разобьем на несколько частей
1. Преобразование условия выпуклости
Определение выпуклости имело вид
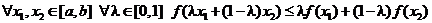 .
.
Пусть 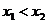 . Обозначим
. Обозначим 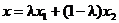 . Так как
. Так как 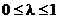 , то
, то 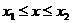 . Далее имеем
. Далее имеем
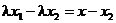 ,
, 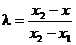 ,
, 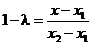 .
.
(Обратите внимание на то, что выражения для l и 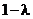 выгоднее сразу писать так, чтобы и в числителе и в знаменателе стояли положительные величины). Условие выпуклости примет вид
выгоднее сразу писать так, чтобы и в числителе и в знаменателе стояли положительные величины). Условие выпуклости примет вид
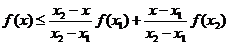 .
.
Так как 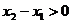 , то имеем
, то имеем
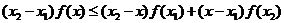 ,
,
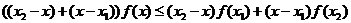 ,
,
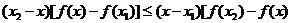 .
.
Так как 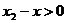 и
и 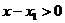 то, деля обе части этого неравенства на
то, деля обе части этого неравенства на 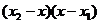 , получим
, получим
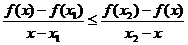 (*)
(*)
при 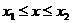 . Именно это неравенство мы и будем использовать в качестве условия выпуклости.
. Именно это неравенство мы и будем использовать в качестве условия выпуклости.
2. Необходимость.
Пусть  выпукла. Сделаем в условии (*) сначала предельный переход
выпукла. Сделаем в условии (*) сначала предельный переход 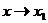 , а затем
, а затем 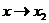 :
:
Предельный переход 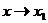 | Предельный переход 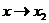 |
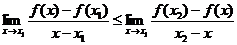 , , 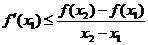 . . | 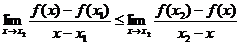 , , 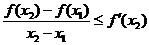 . . |
Сравнивая два последних неравенства мы получим, что 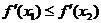 , а так как у нас в самом начале было
, а так как у нас в самом начале было 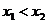 , то это и означает, что
, то это и означает, что 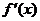 монотонно возрастает.
монотонно возрастает.
3. Достаточность. Пусть 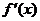 монотонно возрастает. Тогда, по формуле Лагранжа
монотонно возрастает. Тогда, по формуле Лагранжа
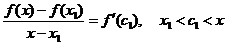 ,
,
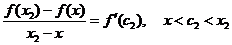 .
.
Так как получилось, что 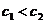 , то
, то  и, следовательно,
и, следовательно,
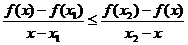 ,
,
что и говорит о том, что  - выпуклая функция.
- выпуклая функция.
Следствие. Пусть 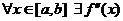 . Тогда для того, чтобы
. Тогда для того, чтобы  была выпуклой необходимо и достаточно, чтобы
была выпуклой необходимо и достаточно, чтобы 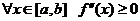 .
.
Доказательство
1.  выпукла Þ
выпукла Þ 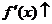 Þ
Þ 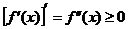 ;
;
2. 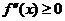 Þ
Þ 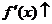 Þ
Þ  выпукла.
выпукла.
Связь выпуклости функции с ее касательной
Теорема. Пусть  определена на
определена на 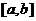 ив каждой точке этого промежутка существует
ив каждой точке этого промежутка существует 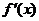 . Тогда для того, чтобы
. Тогда для того, чтобы  была выпуклой необходимо и достаточно, чтобы ее график лежал над касательной, проведенной к любой ее точке.
была выпуклой необходимо и достаточно, чтобы ее график лежал над касательной, проведенной к любой ее точке.
Доказательство.
1. Уравнение касательной.
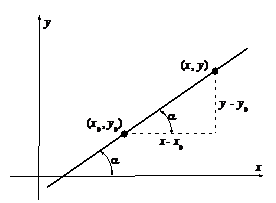 | Рассмотрим уравнение прямой, проходящей через точку 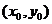 . Пусть . Пусть 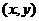 есть некоторая точка, лежащая на нашей прямой. Тогда есть некоторая точка, лежащая на нашей прямой. Тогда 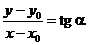 , где a - угол наклона прямой к оси ОХ. , где a - угол наклона прямой к оси ОХ. |
Вернемся теперь к нашей кривой. Пусть 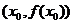 есть некоторая точка, лежащая на нашей кривой. Как было показано в главе 4, для касательной к кривой
есть некоторая точка, лежащая на нашей кривой. Как было показано в главе 4, для касательной к кривой 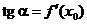 , поэтому уравнение касательной к точке
, поэтому уравнение касательной к точке 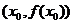 имеет вид
имеет вид
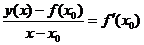 ,
,
которое в стандартной форме пишут так:
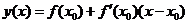 .
.
Вернемся теперь к доказательству теоремы.
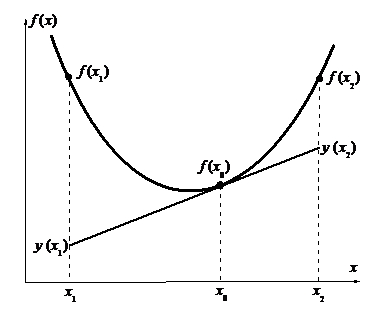
2. Необходимость.
Пусть  выпукла. Тогда ее производная
выпукла. Тогда ее производная 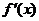 монотонно возрастает. Пусть
монотонно возрастает. Пусть 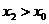 . Тогда
. Тогда
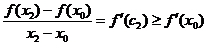
так как 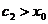 . Так как
. Так как 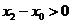 , то имеем
, то имеем
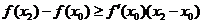 ,
,
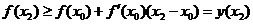
что и говорит о том, что точка кривой лежит выше соответствующей точки касательной.
Пусть теперь 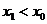 . Тогда
. Тогда
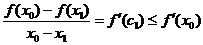
так как 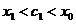 и
и 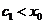 . Так как
. Так как 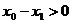 , то
, то
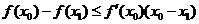 ,
,
откуда получаем
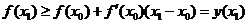
то есть снова точка кривой лежит выше соответствующей точки касательной.
Итак, в любом случае получилось, что 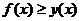 , то есть график функции лежит над касательной.
, то есть график функции лежит над касательной.
3. Достаточность.
Пусть график функции лежит над касательной, то есть 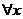
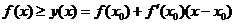 .
.
Возьмем 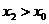 . Тогда
. Тогда
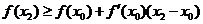 ,
, 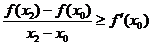 .
.
Возьмем 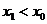 . Тогда
. Тогда
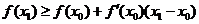 ,
, 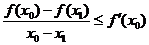 ,
,
так как в этом случае 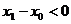 , а при делении на отрицательное число неравенство меняет знак. Сравнивая оба неравенства получим, что для
, а при делении на отрицательное число неравенство меняет знак. Сравнивая оба неравенства получим, что для 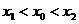
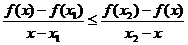 ,
,
а это и есть условие выпуклости, так как по условию теоремы точка 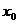 произвольна.
произвольна.
Точки перегиба.
Определение. Точка 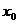 называется точкой перегиба функции
называется точкой перегиба функции  , если она отделяет участок, где функция выпукла от участка, где функция вогнута.
, если она отделяет участок, где функция выпукла от участка, где функция вогнута.
Рассмотрим, как выглядит на графике точка перегиба. Пусть левее точки 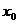 функция выпукла, а правее
функция выпукла, а правее 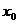 - вогнута. Тогда левее точки
- вогнута. Тогда левее точки 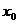 график функции лежит над касательной, а правее
график функции лежит над касательной, а правее 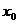 - под касательной. Точка перегиба
- под касательной. Точка перегиба 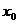 характеризуется тем, что здесь кривая переходит с одной стороны касательной на другую ее сторону, то есть кривая пересекает касательную. То же самое будет, если левее
характеризуется тем, что здесь кривая переходит с одной стороны касательной на другую ее сторону, то есть кривая пересекает касательную. То же самое будет, если левее 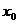 функция
функция  вогнута, а правее
вогнута, а правее 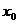 - выпукла.
- выпукла.
Точки перегиба являются характерными точками графика функции, и их нахождение является одной из процедур исследования графика.
 |  |
