Схема исследования функции на экстремумы

Чтобы исследовать экстремумы функции надо сделать следующее:

1. Найти те точки 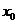, в которых 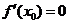. Это будут точки, «подозрительные» на наличие в них экстремума.

2. В точках, где 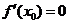, найти первую по порядку старшинства производную, отличную от нуля. Если это будет производная четного порядка, то в точке 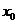- локальный экстремум (если эта производная отрицательная - то максимум, если положительная - то минимум); если же нечетного порядка - в точке 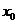экстремума нет.

3. Найти те точки, где существуют лишь односторонние производные. Если эти производные разных знаков - в точке локальный экстремум, если одного знака - экстремума нет.

4. Найти производные на границах области задания функции и определить, как ведет себя функция на границе.

5. Вычислить значения функции в точках локальных минимумов и максимумов и найти глобальный минимум (наименьший из локальных минимумов) и глобальный максимум (наибольший из локальных максимумов).

Выпуклые и вогнутые функции.

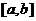Определение. Функция называется выпуклой (или выпуклой вниз) на отрезке если

.

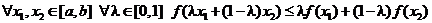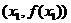Выясним, как выглядит график выпуклой функции. Отметим на графике функции точки и 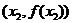. Тогда точка с координатам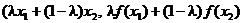и при 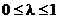лежит на отрезке, соединяющем точк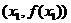и и 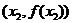, то есть множество точек 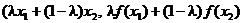, 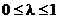есть секущая, соединяющая эти две точки. Так как, согласно определению, 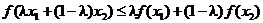, то это означает, что точка графика функции с координатами 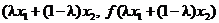лежит ниже соответствующей точки секущей (см. рисунок).

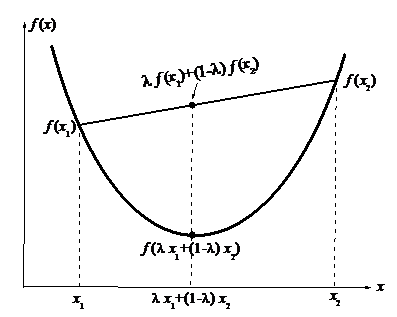
Вид графика выпуклойфункции

Итак, выпуклость функции означает, что график функции лежит ниже секущей, соединяющей любые две ее точки.

Аналогично дается следующее определение.

Определение. Функция называется вогнутой (или выпуклой вверх) на отрезке 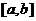, если

.

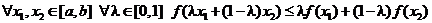График вогнутой функции лежит выше секущей, соединяющей любые две ее точки (см. рисунок) (см. рисунок).

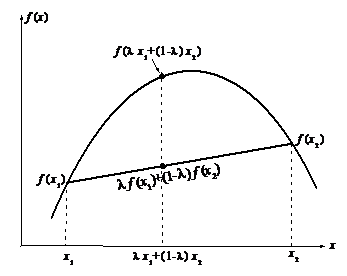
Вид графика вогнутойфункции

Свойства выпуклых функций.

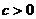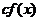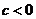1. Если выпукла и , то выпукла. Если выпукла и , то 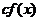вогнута.

Это свойство очевидно.

2. Если и 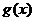выпуклы, то 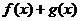выпукла.

Это свойство также очевидно.

3. Выпуклость суперпозиции функций.

Рассмотрим сложную функцию 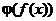. Тогда рассматриваемое свойство может быть представлено в виде следующей таблицы:

Таблица 1.

	j	f	j(f)
1. 2. 3. 4.	Выпукла, ­ Выпукла, ¯ Вогнута, ­ Вогнута, ¯	Выпукла Вогнута Вогнута Выпукла	Выпукла Выпукла Вогнута Вогнута

Докажем, для примера, свойство 1.

Начинаем со свойств функции f:

выпукла Þ .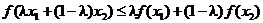

Заканчиваем свойствами функции j в таком порядке: сначала - монотонность, потом - выпуклость-вогнутость:

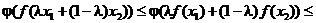(сработала монотонность)

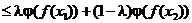(сработала выпуклость функции j).

Сравнивая начало и конец, получаем, что сложная функция j(f) выпукла. <

Остальные свойства доказываются аналогично.

4. Выпуклость-вогнутость обратной функции.

Пусть дана некоторая функция и 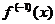есть функция, обратная к ней. Доказываемые свойства приведены в таблице.

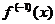1. 2. 3. 4.	Выпукла, ­ Выпукла, ¯ Вогнута, ¯ Вогнута, ­	Вогнута, ­ Выпукла, ¯ Вогнута, ¯ Выпукла, ­

Монотонность обратной функции доказана в главе 3.

Докажем, для примера, свойство 1. Так как, если 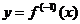, то 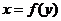, мы имеем:

, ;

, .

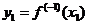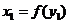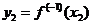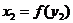Сначала срабатывает выпуклость функции :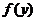

.

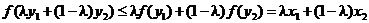Перепишем это неравенство в обратном порядке

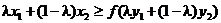
и подействуем на него обратной функцией. У нее срабатывает свойство монотонности:

.

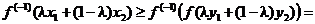
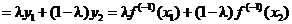Сравнивая начало и конец, получаем, что обратная функция вогнута. <

Остальные свойства доказываются аналогично.

5. Основным свойством выпуклых функций является так называемое

Неравенство Иенсена. Пусть - выпуклая на 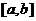функция. Тогда 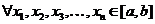и 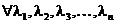таких, что

а) ;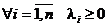

б)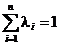

верно неравенство

.

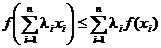Доказательство проведем методом индукции.

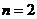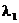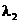1.В случае , когда имеем и такие, что 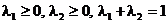имеем

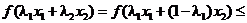(согласно определения)

,

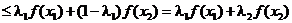то есть для 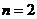неравенство Иенсена верно.

2. Пусть неравенство Иенсена верно для некоторого п. Докажем, что оно верно и для .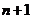

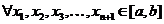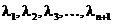Возьмем и , такие что 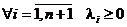и 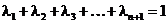. Рассмотрим комбинацию

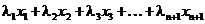
в которой 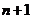слагаемое. Чтобы сделать п слагаемых объединим два последних слагаемых в одно

,

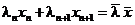где 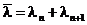и .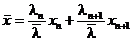

Тогда 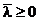, 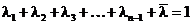и мы получаем

,

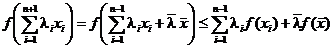так как в аргументе 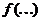стало уже п слагаемых а мы предположили, что для п слагаемых неравенство Иенсена верно. Но далее мы имеем, согласно определения выпуклой функции,

.

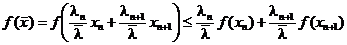Поэтому, продолжая предыдущее неравенство, напишем

,

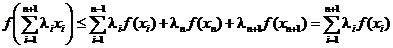что и доказывает справедливость неравенства Иенсена для 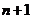. <