Глава 5. Применение производных
Глава 5. Применение производных
Правило Лопиталя.
Среди неопределенных выражений чаще всего приходится встречаться с неопределенностями типа 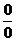 или
или 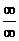 . При их раскрытии очень помогает так называемое правило Лопиталя.
. При их раскрытии очень помогает так называемое правило Лопиталя.
Раскрытие неопределенностей типа 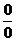 .
.
Теорема 1. Пусть
а) функции  и
и 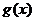 определены и непрерывны на
определены и непрерывны на 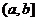 ;
;
б) в 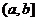 существуют
существуют 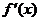 и
и 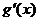 , причем
, причем 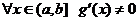 ;
;
в) 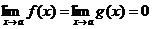 ;
;
г) 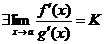 .
.
Тогда 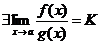 .
.
Доказательство.
В точке а функции  и
и 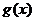 не определены. Доопределим их по непрерывности, полагая
не определены. Доопределим их по непрерывности, полагая 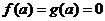 . Тогда по формуле Коши
. Тогда по формуле Коши
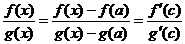 ,
,
где 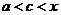 . Поэтому при
. Поэтому при 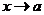 также будет
также будет 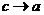 . Переходя к пределу, получим
. Переходя к пределу, получим
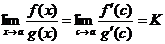 ,
,
так как последний предел существует. <
Теорема 2.
Пусть
а) функции  и
и 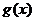 определены и непрерывны на
определены и непрерывны на 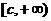 ;
;
б) в 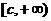 существуют
существуют 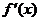 и
и 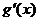 , причем
, причем 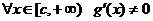 ;
;
в) 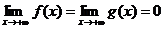 ;
;
г) 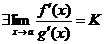 .
.
Тогда 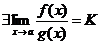 .
.
Доказательство.Сделаем «замену переменной» 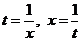 . Тогда при
. Тогда при 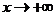
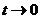 и мы можем воспользоваться предыдущей теоремой. Имеем
и мы можем воспользоваться предыдущей теоремой. Имеем
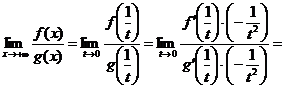
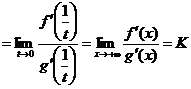 ,
,
что и доказывает теорему. <
Несмотря на свою внешнюю простоту, правило Лопиталя довольно сложно при его практическом использовании. При практическом применении этого правила следует иметь в виду следующие рекомендации:
а) прежде, чем находить 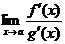 рекомендуется выражение
рекомендуется выражение 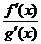 упрощать, насколько это возможно;
упрощать, насколько это возможно;
б) если при вычислении 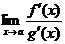 снова подучилась неопределенность, то применить правило Лопиталя еще раз. Однако перед его повторным применением рекомендуется выделить отдельно сомножители, не стремящиеся к нулю, и заменить их предельными значениями.
снова подучилась неопределенность, то применить правило Лопиталя еще раз. Однако перед его повторным применением рекомендуется выделить отдельно сомножители, не стремящиеся к нулю, и заменить их предельными значениями.
Рассмотрим два примера на эти рекомендации.
Пример 1.
Вычислить 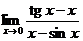 .
.
Решение. Используем правило Лопиталя. Имеем
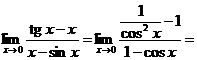
И вот тут не имеет смысла сразу подставлять 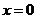 , так как снова получилась неопределенность. Не имеет также смысла сразу применять правило Лопиталя еще раз - залезем в такие дебри, из которых не выберемся. Поэтому сначала упрощаем - убираем «трехэтажность» и сокращаем сомножитель
, так как снова получилась неопределенность. Не имеет также смысла сразу применять правило Лопиталя еще раз - залезем в такие дебри, из которых не выберемся. Поэтому сначала упрощаем - убираем «трехэтажность» и сокращаем сомножитель 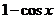 :
:
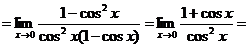
И вот тут уже можно смело подставить 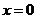 , так как нет никакой неопределенности:
, так как нет никакой неопределенности:
=2.
Пример 2.
Вычислить 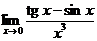 .
.
Решение. Используем правило Лопиталя и упрощаем. Имеем
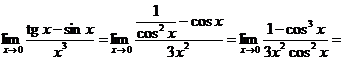
У нас снова получилась неопределенность. Но, прежде чем применять правило Лопиталя еще раз, надо сначала выделить сомножители, не стремящиеся к 0, и вычислить их предел отдельно:
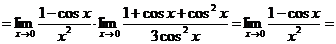
А вот теперь к оставшемуся выражению применяем правило Лопиталя еще два раза:
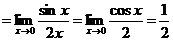 .
.
Раскрытие неопределенностей типа 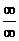 .
.
Теорема. Пусть
а) функции  и
и 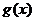 определены и непрерывны на
определены и непрерывны на 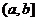 ;
;
б) в 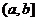 существуют
существуют 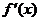 и
и 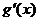 , причем
, причем 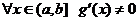 ;
;
в) 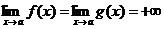 ;
;
г) 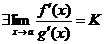 .
.
Тогда 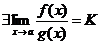 .
.
Доказательство.
Ввиду громоздкости доказательства, разобьем его на части.
А) Избавление от производных.
В условии теоремы сказано, что 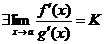 . Это значит, что
. Это значит, что
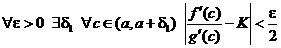 .
.
Возьмем х и х0 так, чтобы было 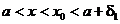 . Тогда, по формуле Коши,
. Тогда, по формуле Коши,
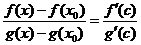 ,
,
и 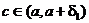 . Поэтому для этих х и х0 имеем
. Поэтому для этих х и х0 имеем
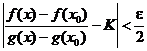 .
.
В дальнейшем х0 фиксируем.
Б) Полезное соотношение.
Имеем, раскрывая скобки,
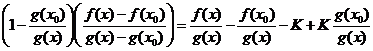 .
.
Исходное выражение взято «с потолка». Отсюда получаем
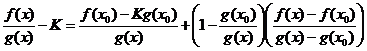 .
.
В) Предельный переход.
При 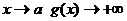 . Поэтому
. Поэтому
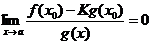 .
.
Это означает, что
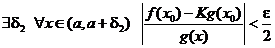 .
.
Берем 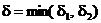 . Тогда
. Тогда 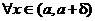
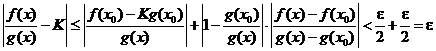 ,
,
так как 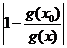 <1. Это, по определению предела, и означает, что
<1. Это, по определению предела, и означает, что 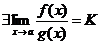 .<
.<
Заметим, что правило Лопиталя позволяет раскрывать и неопределенности типа 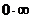 , если произведение
, если произведение 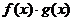 привести к виду
привести к виду 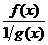 или
или 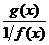 .
.
Заметим еще, что обратное, вообще говоря, не верно: из существования предела отношения 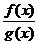 не следует существование предела отношения
не следует существование предела отношения 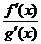 .
.
Экстремумы функции.
Определение 1. Говорят, что в точке x0 функция  имеет локальный максимум (локальный минимум), если
имеет локальный максимум (локальный минимум), если
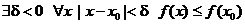 (
( 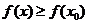 ).
).
В этом определении обратите внимание на слово «локальный». Оно означает, что  принимает свое наибольшее значение в точке x0 только по отношению к отрезку
принимает свое наибольшее значение в точке x0 только по отношению к отрезку 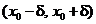 . Вне этого отрезка о поведении функции ничего не утверждается: она может принять там и значение, большее чем
. Вне этого отрезка о поведении функции ничего не утверждается: она может принять там и значение, большее чем 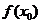 . То же самое можно сказать и по отношению к локальному минимуму (см. рис.).
. То же самое можно сказать и по отношению к локальному минимуму (см. рис.).
 |  |
Определение 2. Говорят, что функция  имеет в точке x0 глобальный максимум (минимум) на множестве Х, если
имеет в точке x0 глобальный максимум (минимум) на множестве Х, если 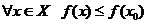
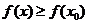 .
.
Термины «максимум» и «минимум» объединяют одним словом «экстремум» и говорят о локальном или глобальном экстремуме. Отметьте еще, что для непрерывной функции локальные максимумы или минимумы чередуются.

Нахождение локальных экстремумов - одна из важнейших задач исследования функций имеющая большое практическое значение. Перейдем к ее изучению.
Пусть функция  определена на некотором отрезке
определена на некотором отрезке 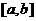 . Научимся сначала находить локальные экстремумы, расположенные внутри этого отрезка.
. Научимся сначала находить локальные экстремумы, расположенные внутри этого отрезка.
Граничные точки
Рассмотрим, наконец, граничные точки a и b отрезка 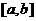 . Здесь поведение функции
. Здесь поведение функции  может быть следующим:
может быть следующим:
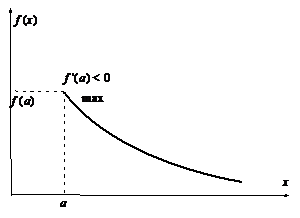 | 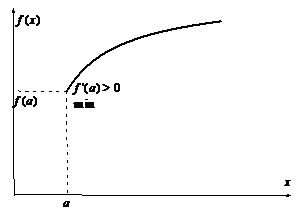 |
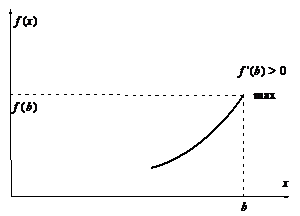 | 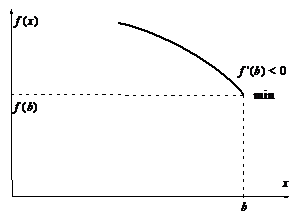 |
Таким образом, то, что мы имеем в граничных точках, определяется знаком первой производной.
Подведем итоги.
Свойства выпуклых функций.
1. Если  выпукла и
выпукла и 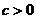 , то
, то 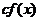 выпукла. Если
выпукла. Если  выпукла и
выпукла и 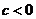 , то
, то 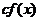 вогнута.
вогнута.
Это свойство очевидно.
2. Если  и
и 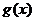 выпуклы, то
выпуклы, то 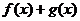 выпукла.
выпукла.
Это свойство также очевидно.
3. Выпуклость суперпозиции функций.
Рассмотрим сложную функцию 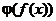 . Тогда рассматриваемое свойство может быть представлено в виде следующей таблицы:
. Тогда рассматриваемое свойство может быть представлено в виде следующей таблицы:
Таблица 1.
| j | f | j(f) | |
| 1. 2. 3. 4. | Выпукла, Выпукла, ¯ Вогнута, Вогнута, ¯ | Выпукла Вогнута Вогнута Выпукла | Выпукла Выпукла Вогнута Вогнута |
Докажем, для примера, свойство 1.
Начинаем со свойств функции f:
 выпукла Þ
выпукла Þ 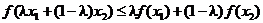 .
.
Заканчиваем свойствами функции j в таком порядке: сначала - монотонность, потом - выпуклость-вогнутость:
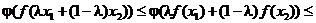 (сработала монотонность)
(сработала монотонность)
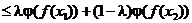 (сработала выпуклость функции j).
(сработала выпуклость функции j).
Сравнивая начало и конец, получаем, что сложная функция j(f) выпукла. <
Остальные свойства доказываются аналогично.
4. Выпуклость-вогнутость обратной функции.
Пусть дана некоторая функция  и
и 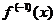 есть функция, обратная к ней. Доказываемые свойства приведены в таблице.
есть функция, обратная к ней. Доказываемые свойства приведены в таблице.
 | 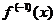 | |
| 1. 2. 3. 4. | Выпукла, Выпукла, ¯ Вогнута, ¯ Вогнута, | Вогнута, Выпукла, ¯ Вогнута, ¯ Выпукла, |
Монотонность обратной функции доказана в главе 3.
Докажем, для примера, свойство 1. Так как, если 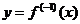 , то
, то 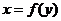 , мы имеем:
, мы имеем:
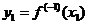 ,
, 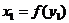 ;
;
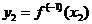 ,
, 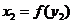 .
.
Сначала срабатывает выпуклость функции 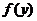 :
:
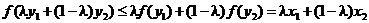 .
.
Перепишем это неравенство в обратном порядке
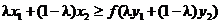
и подействуем на него обратной функцией. У нее срабатывает свойство монотонности:
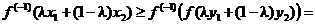
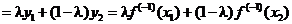 .
.
Сравнивая начало и конец, получаем, что обратная функция вогнута. <
Остальные свойства доказываются аналогично.
5. Основным свойством выпуклых функций является так называемое
Неравенство Иенсена. Пусть  - выпуклая на
- выпуклая на 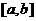 функция. Тогда
функция. Тогда 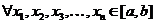 и
и 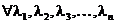 таких, что
таких, что
а) 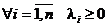 ;
;
б) 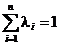
верно неравенство
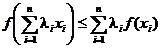 .
.
Доказательство проведем методом индукции.
1.В случае 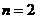 , когда имеем
, когда имеем 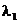 и
и 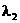 такие, что
такие, что 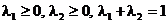 имеем
имеем
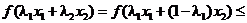 (согласно определения)
(согласно определения)
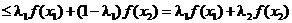 ,
,
то есть для 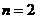 неравенство Иенсена верно.
неравенство Иенсена верно.
2. Пусть неравенство Иенсена верно для некоторого п. Докажем, что оно верно и для 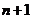 .
.
Возьмем 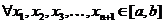 и
и 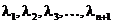 , такие что
, такие что 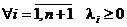 и
и 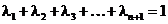 . Рассмотрим комбинацию
. Рассмотрим комбинацию
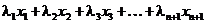
в которой 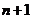 слагаемое. Чтобы сделать п слагаемых объединим два последних слагаемых в одно
слагаемое. Чтобы сделать п слагаемых объединим два последних слагаемых в одно
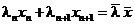 ,
,
где 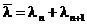 и
и 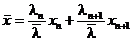 .
.
Тогда 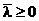 ,
, 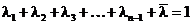 и мы получаем
и мы получаем
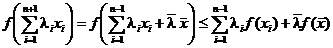 ,
,
так как в аргументе 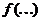 стало уже п слагаемых а мы предположили, что для п слагаемых неравенство Иенсена верно. Но далее мы имеем, согласно определения выпуклой функции,
стало уже п слагаемых а мы предположили, что для п слагаемых неравенство Иенсена верно. Но далее мы имеем, согласно определения выпуклой функции,
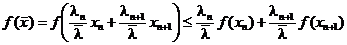 .
.
 Поэтому, продолжая предыдущее неравенство, напишем
Поэтому, продолжая предыдущее неравенство, напишем
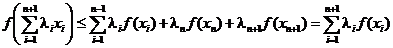 ,
,
что и доказывает справедливость неравенства Иенсена для  . <
. <
Точки перегиба.
Определение. Точка 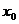 называется точкой перегиба функции
называется точкой перегиба функции  , если она отделяет участок, где функция выпукла от участка, где функция вогнута.
, если она отделяет участок, где функция выпукла от участка, где функция вогнута.
Рассмотрим, как выглядит на графике точка перегиба. Пусть левее точки 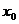 функция выпукла, а правее
функция выпукла, а правее 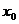 - вогнута. Тогда левее точки
- вогнута. Тогда левее точки 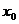 график функции лежит над касательной, а правее
график функции лежит над касательной, а правее 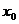 - под касательной. Точка перегиба
- под касательной. Точка перегиба 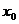 характеризуется тем, что здесь кривая переходит с одной стороны касательной на другую ее сторону, то есть кривая пересекает касательную. То же самое будет, если левее
характеризуется тем, что здесь кривая переходит с одной стороны касательной на другую ее сторону, то есть кривая пересекает касательную. То же самое будет, если левее 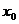 функция
функция  вогнута, а правее
вогнута, а правее 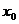 - выпукла.
- выпукла.
Точки перегиба являются характерными точками графика функции, и их нахождение является одной из процедур исследования графика.
 |  |
Асимптоты
Пусть функция  определена на полу бесконечном (типа
определена на полу бесконечном (типа 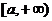 или
или 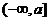 ) или бесконечном интервале.
) или бесконечном интервале.
Горизонтальная асимптота.
Пусть 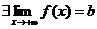 . Тогда говорят, что у функции
. Тогда говорят, что у функции  имеется горизонтальная асимптота
имеется горизонтальная асимптота 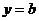 . График функции чаще всего имеет такой вид (при
. График функции чаще всего имеет такой вид (при 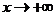 )
)
 |  |
хотя, в принципе, может иметь и такой вид:
 | На рисунке приведен график функции 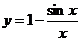 , имеющей асимптоту , имеющей асимптоту 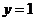 . . |
Вертикальная асимптота.
 |  |
Пусть при 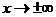
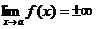 . Тогда говорят, что прямая
. Тогда говорят, что прямая 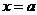 является вертикальной асимптотой
является вертикальной асимптотой  . График функции
. График функции  при приближении х к а ведет себя примерно так, как изображено на рисунках, хотя, конечно, могут быть разные варианты, связанные с тем, куда уходит
при приближении х к а ведет себя примерно так, как изображено на рисунках, хотя, конечно, могут быть разные варианты, связанные с тем, куда уходит  - в +¥ или в -¥
- в +¥ или в -¥
Чаще всего вертикальная асимптота появляется тогда, когда  имеет вид
имеет вид
 .
.
Тогда вертикальные асимптоты находятся как корни уравнения 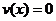 .
.
Наклонные асимптоты.
Характерной чертой и горизонтальной и вертикальной асимптот было то, что это прямые линии, к которым «приближается» график  . В общем случае асимптота - это некоторая прямая, к которой неограниченно приближается функция
. В общем случае асимптота - это некоторая прямая, к которой неограниченно приближается функция  при
при 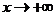 или
или 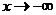 .
.
 | Пусть уравнение асимптот есть 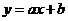 . Значение функции при аргументе х есть . Значение функции при аргументе х есть  . Неограниченное приближение к асимптоте означает, что величина . Неограниченное приближение к асимптоте означает, что величина 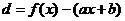 стремится к 0 при стремится к 0 при 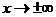 : : 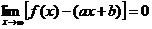 . (*) Если эта величина стремиться к нулю, то тем более стремиться к нулю величина: . (*) Если эта величина стремиться к нулю, то тем более стремиться к нулю величина: 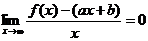 . Но тогда мы имеем . Но тогда мы имеем |
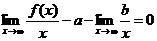 ,
,
и так как последний предел равен нулю, то
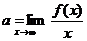 .
.
Зная а, можно найти и b из исходного соотношения (*):
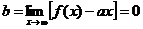 .
.
Тем самым параметры асимптоты полностью определяются.
Пример. Пусть, например, 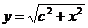 .
.
Тогда
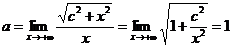 ,
, 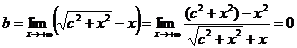 ,
,
то есть асимптота при  имеет уравнение
имеет уравнение 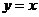 .
.
Аналогично можно показать, что при 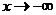 асимптота имеет вид
асимптота имеет вид 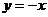 .
.
Сам график функции 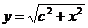 выглядит так:
выглядит так:

Глава 5. Применение производных
Правило Лопиталя.
Среди неопределенных выражений чаще всего приходится встречаться с неопределенностями типа 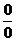 или
или 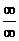 . При их раскрытии очень помогает так называемое правило Лопиталя.
. При их раскрытии очень помогает так называемое правило Лопиталя.
Раскрытие неопределенностей типа 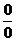 .
.
Теорема 1. Пусть
а) функции  и
и 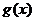 определены и непрерывны на
определены и непрерывны на 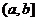 ;
;
б) в 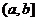 существуют
существуют 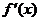 и
и 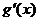 , причем
, причем 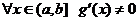 ;
;
в) 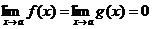 ;
;
г) 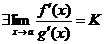 .
.
Тогда 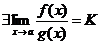 .
.
Доказательство.
В точке а функции  и
и 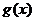 не определены. Доопределим их по непрерывности, полагая
не определены. Доопределим их по непрерывности, полагая 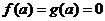 . Тогда по формуле Коши
. Тогда по формуле Коши
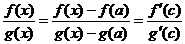 ,
,
где 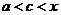 . Поэтому при
. Поэтому при 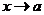 также будет
также будет 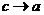 . Переходя к пределу, получим
. Переходя к пределу, получим
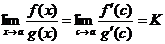 ,
,
так как последний предел существует. <
Теорема 2.
Пусть
а) функции  и
и 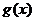 определены и непрерывны на
определены и непрерывны на 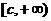 ;
;
б) в 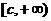 существуют
существуют 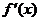 и
и 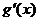 , причем
, причем 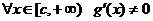 ;
;
в) 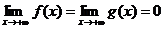 ;
;
г) 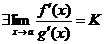 .
.
Тогда 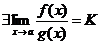 .
.
Доказательство.Сделаем «замену переменной» 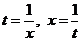 . Тогда при
. Тогда при 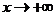
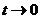 и мы можем воспользоваться предыдущей теоремой. Имеем
и мы можем воспользоваться предыдущей теоремой. Имеем
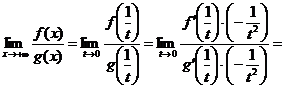
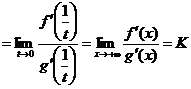 ,
,
что и доказывает теорему. <
Несмотря на свою внешнюю простоту, правило Лопиталя довольно сложно при его практическом использовании. При практическом применении этого правила следует иметь в виду следующие рекомендации:
а) прежде, чем находить 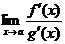 рекомендуется выражение
рекомендуется выражение 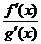 упрощать, насколько это возможно;
упрощать, насколько это возможно;
б) если при вычислении 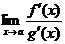 снова подучилась неопределенность, то применить правило Лопиталя еще раз. Однако перед его повторным применением рекомендуется выделить отдельно сомножители, не стремящиеся к нулю, и заменить их предельными значениями.
снова подучилась неопределенность, то применить правило Лопиталя еще раз. Однако перед его повторным применением рекомендуется выделить отдельно сомножители, не стремящиеся к нулю, и заменить их предельными значениями.
Рассмотрим два примера на эти рекомендации.
Пример 1.
Вычислить 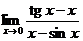 .
.
Решение. Используем правило Лопиталя. Имеем
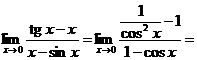
И вот тут не имеет смысла сразу подставлять 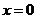 , так как снова получилась неопределенность. Не имеет также смысла сразу применять правило Лопиталя еще раз - залезем в такие дебри, из которых не выберемся. Поэтому сначала упрощаем - убираем «трехэтажность» и сокращаем сомножитель
, так как снова получилась неопределенность. Не имеет также смысла сразу применять правило Лопиталя еще раз - залезем в такие дебри, из которых не выберемся. Поэтому сначала упрощаем - убираем «трехэтажность» и сокращаем сомножитель 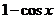 :
:
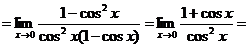
И вот тут уже можно смело подставить 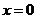 , так как нет никакой неопределенности:
, так как нет никакой неопределенности:
=2.
Пример 2.
Вычислить 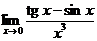 .
.
Решение. Используем правило Лопиталя и упрощаем. Имеем
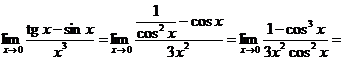
У нас снова получилась неопределенность. Но, прежде чем применять правило Лопиталя еще раз, надо сначала выделить сомножители, не стремящиеся к 0, и вычислить их предел отдельно:
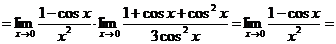
А вот теперь к оставшемуся выражению применяем правило Лопиталя еще два раза:
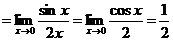 .
.
Раскрытие неопределенностей типа 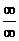 .
.
Теорема. Пусть
а) функции  и
и 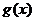 определены и непрерывны на
определены и непрерывны на 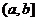 ;
;
б) в 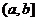 существуют
существуют 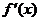 и
и 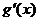 , причем
, причем 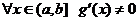 ;
;
в) 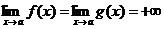 ;
;
г) 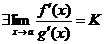 .
.
Тогда 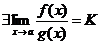 .
.
Доказательство.
Ввиду громоздкости доказательства, разобьем его на части.
А) Избавление от производных.
В условии теоремы сказано, что 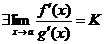 . Это значит, что
. Это значит, что
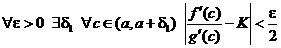 .
.
Возьмем х и х0 так, чтобы было 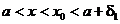 . Тогда, по формуле Коши,
. Тогда, по формуле Коши,
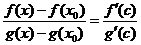 ,
,
и 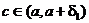 . Поэтому для этих х и х0 имеем
. Поэтому для этих х и х0 имеем
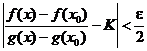 .
.
В дальнейшем х0 фиксируем.
Б) Полезное соотношение.
Имеем, раскрывая скобки,
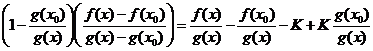 .
.
Исходное выражение взято «с потолка». Отсюда получаем
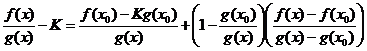 .
.
В) Предельный переход.
При 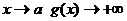 . Поэтому
. Поэтому
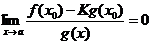 .
.
Это означает, что
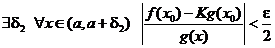 .
.
Берем 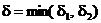 . Тогда
. Тогда 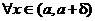
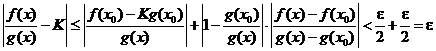 ,
,
так как 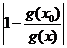 <1. Это, по определению предела, и означает, что
<1. Это, по определению предела, и означает, что 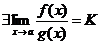 .<
.<
Заметим, что правило Лопиталя позволяет раскрывать и неопределенности типа 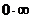 , если произведение
, если произведение 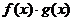 привести к виду
привести к виду 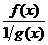 или
или 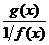 .
.
Заметим еще, что обратное, вообще говоря, не верно: из существования предела отношения 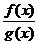 не следует существование предела отношения
не следует существование предела отношения 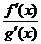 .
.
