Непрерывность элементарных функций.

Разумеется, имеется бесконечно много разных функций. Однако среди них выделяется класс элементарных функций. К ним относятся:

а) показательная функция ;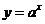

б) гиперболические функции sh(x), ch(x), th(x);

в) логарифмическая функция у=log_a(x);

а) степенная функция ;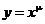

д) тригонометрические функции sin(x), cos(x), tg(x);

е) обратные тригонометрические функции arc sin(x), arc cos(x), arc tg(x).

Все возможные суперпозиции этих функций также называются элементарными.

Далее мы сделаем небольшой обзор свойств этих функций, особо обращая внимание на их непрерывность.

Показательная функция.

.

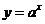Мы не будем давать строгого определения показательной функции, так как изложенного выше материала для этого недостаточно. Будут изучены лишь свойства этой функции.

Рассмотрим подробно случай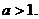

1. Основное свойство показательной функции имеет вид

.

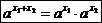Иногда именно это свойство принимается в качестве определения показательной функции, так как можно показать, что среди непрерывных функций показательная функция – единственная функция, удовлетворяющая свойству 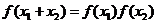. Следствием этого свойства является следующее свойство показательной функции: .

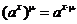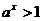2. Если , то ; при любых значениях х .

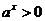3. При 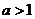функция 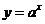строго монотонно возрастает.

Пусть 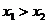. Тогда 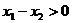и мы имеем

,

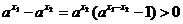так как 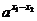>1. Следовательно .

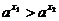4. .

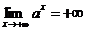Представим а в виде а =1 + l. Тогда l>0.

Пусть х = n где n - целое положительное число. Тогда, используя формулу бинома Ньютона, получим

.

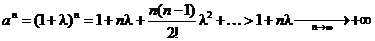Следовательно .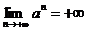

Пусть теперь х > 0 и n = [x] есть целая часть х. Тогда 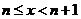; при х®+¥ также и n®+¥ и мы имеем

.

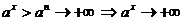5. .

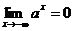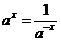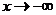
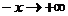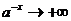Действительно, . При , и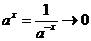

6 . 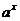непрерывна при любом х.

Пусть 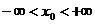. Возьмем любое 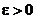и найдем такое целое число n, чтобы выполнялось соотношение

.

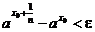Можно ли это сделать?

Имеем следующую цепочку неравенств.

;

;

;

;

.

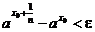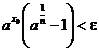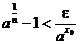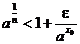Поэтому, если мы добьемся выполнения неравенства

,

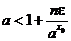то предыдущее неравенство будет и подавно выполнено. Но последнее неравенство верно при

,

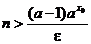так что искомое n всегда существует.

Но тогда, при х, удовлетворяющем неравенству

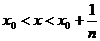
имеем

,

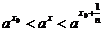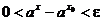
и функция a^x непрерывна в точке х₀ справа.

Аналогично доказывается, что функция a^x непрерывна в точке х₀ слева, и поэтому функция a^x непрерывна в точке х₀.

7. Значения функции a^x заполняют сплошь отрезок (0, +¥).

Случай 0 < a < 1 рассматривается аналогично. В этом случае функция a^x строго монотонно убывает, непрерывна при любых х, и 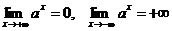. Ее значения также заполняют сплошь отрезок (0, +¥).

Вид графика показательной функции при а > 1 и при 0 < a < 1 приведен на рисунке.

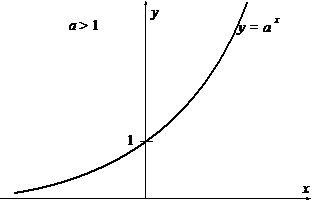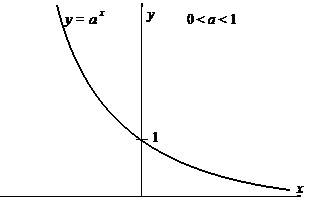Математики особенно «любят» функцию 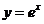, то есть показательную функцию при а=е. Ее называют экспоненциальной функцией, или просто экспонентой. Для нее часто используют обозначение .

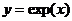Гиперболические функции.

С функцией e^x тесно связаны функции, получившие название гиперболических. К ним относятся:

гиперболический синус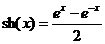

гиперболический косинус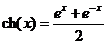

гиперболический тангенс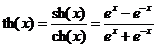

Рассмотрим коротко свойства этих функций.

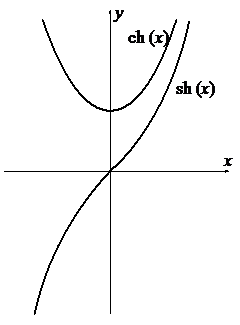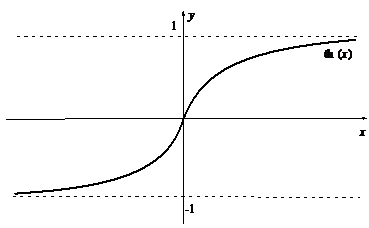1. Область определения этих функций -¥<x<+¥

2. sh(-x)= –sh(x), th(-x)= –th(x), ch(-x)= ch(x), то есть sh(x) и th(x) являются нечетными функциями, а ch(x) – четной функцией. Графики их изображены на рисунках.

3. sh(х), ch(x) и th(x) непрерывны для всех х.

4. sh(x) и th(x) монотонно возрастают.

5. Выведем основные формулы, касающиеся этих функций, и очень напоминающие формулы тригонометрии.

а) ch²(x) - sh²(x)=1.

Действительно,

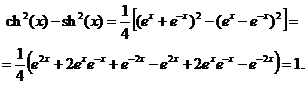
б)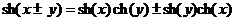

Вывод этой формулы надо вести с правой части. Имеем:

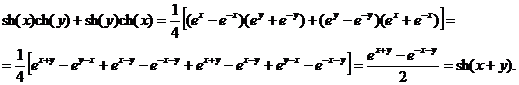
в) .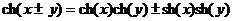

Аналогично имеем:

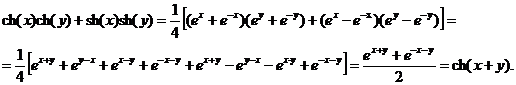
Аналогично выводятся формулы и для комбинации 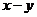. Можно вывести и много других формул, аналогичных формулам геометрии.

Логарифмическая функция

Функция, обратная a^x, называется логарифмической функцией, и обозначается log_ax. Ее свойства получаются как следствия свойств функции a^x

а) а > 1.

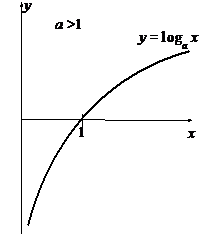1. Так как. значения axÎ(0; +¥), то logax определена для 0<x<+¥. 2. Так как ax строго монотонно возрастает, то logax тоже строго монотонно возрастает. 3. Так как ax непрерывна, то и logax тоже непрерывна. 4. 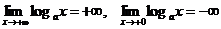. 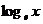называется натуральным логарифмом и обозначается ln(x).

б) 0 < а < 1

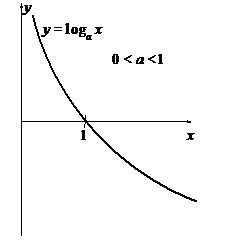1. log ax определена для 0<x<+¥. 2. log ax строго монотонно убывает. 3. log ax непрерывна. 4. .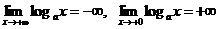

Основное свойство логарифмической функции имеет вид:

.

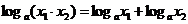Докажем это свойство. Действительно, используя тот факт, что логарифмическая функция является функцией, обратной показательной, мы можем записать

, .

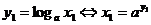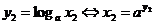Но тогда, используя основное свойство показательной функции, получаем

.

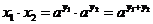Снова используя тот факт, что логарифмическая функция является функцией, обратной показательной, получаем

,

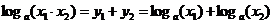что и требовалось доказать.

Можно показать, что log_ax – единственная непрерывная функция, удовлетворяющая свойству .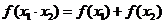

Другие важные формулы, касающиеся логарифмической функции

а) ;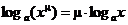

б) .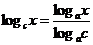

Степенная функция

Функция 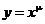где m – произвольное вещественное число, называется степенной функцией. В общем случае она определяется следующим образом:

.

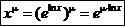Из этого определения следуют и все ее свойства.

1. Так как функция 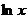определена для 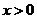, то и степенная функция в общем случае определена лишь для 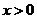(хотя для случая, когда m - целое число, ее определяют и для отрицательных значений х).

2. 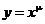- непрерывная функция, как суперпозиция непрерывных функций.

3. Монотонность.

Имеем для :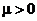

,

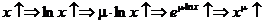то есть при 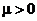степенная функция является строго монотонно возрастающей функцией.

Аналогично, для ,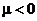

,

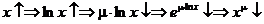то есть при 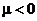степенная функция является строго монотонно убывающей функцией.

4. Поведение 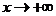при и при .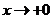

Имеем для :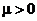

,

.

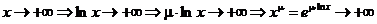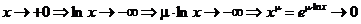Аналогично, для ,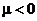

,

.

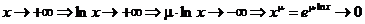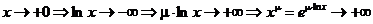Тригонометрические функции

Так как эти функции подробно изучаются в школе, то напоминать их свойства мы не будем. Рассмотрим лишь вопрос об их непрерывности. Основным здесь для нас будет неравенство 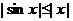, которое мы примем без доказательства.

Функция sin x .

Имеем

,

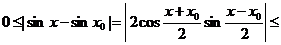
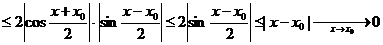так что sin x₀ непрерывен при любом х₀.

Функция cos x.

Аналогично предыдущему, имеем

,

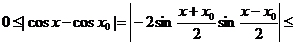
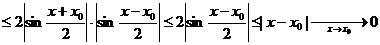так что cos x₀ непрерывен при любом х₀.

Функция tg x.

Так как функции sin(x) и cos(x) непрерывны для всех x, то 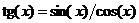имеет разрывы второго рода в точках, где cos(x)=0, то есть в точках 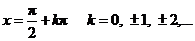При остальных значениях аргумента tg(x) непрерывен.