Свойства непрерывных функций. Непрерывность сложной функции.

Определения.

Определение 1. Функция f(x) называется непрерывной в точке х₀, если .

Дадим несколько расшифровок этого важнейшего определения.

а) Вспоминая понятие предела, запишем непрерывность f(x) в точке х₀ в виде

.

б) Так как , то непрерывность в точке х₀ можно записать в виде

.

Отсюда следует важнейшее свойство непрерывной функции: для непрерывной функции можно переставлять местами знак функции и знак предельного перехода

в) Обозначим Dx=x-x₀ (приращение аргумента) и Df=f(x) - f(x₀) (приращение функции). Тогда непрерывность в точке х₀ означает, что , то есть бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции.

Ведем обозначения:

,

если эти пределы существуют.

Определение 2. Функция f(x) называется непрерывной в точке х₀ слева (справа) если f(x₀)=f(x₀ – 0) (f(x₀)=f(x₀+0)). Очевидно, что непрерывность в точке х₀ означает непрерывность слева и справа одновременно.

Определение 3. Функция f(x) называется непрерывной на некотором множестве Х, если она непрерывна в каждой точке этого множества, то есть если

Обратите внимание, где стоит квантор , это важно.

Определение. Если функция f(x) не является непрерывной в точке х₀, то говорят, что в точке х₀ функция f(x) имеет разрыв.

Типы разрывов.

А.Пусть существуют конечные f(x0-0) и f(x0+0), они равны друг другу, но не равны значению функции в точке х0, то есть выполнено условие f(x0-0) = f(x0+0) ≠ f(x0), то говорят, что в точке х0 функция f(x) имеет устранимый разрыв. Действительно, достаточно изменить значение функции в точке х0 и разрыв исчезнет. Вид графика функции в этом случае приведен на рисунке.

В. Пусть существуют конечные f(x₀-0) и f(x₀+0), но они не равны друг другу . Тогда говорят, что в точке х₀ функция f(x) имеет разрыв I рода или скачок.

График функции f(x) в окрестности точки х₀ имеет в этом случае примерно такой вид:

Величина |f(x₀+0)-f(x₀-0)| называется величиной скачка функции f(x) в точке х₀.

В. Если хотя бы один из пределов или бесконечен или не существует, то говорят, что в точке х₀ функция f(x) имеет разрыв второго рода.

Виды графика функции f(x) в окрестности точки х₀ в этом случае гораздо разнообразнее. Некоторые возможные варианты приведены ниже.

, ,

, ,

,	; и не существуют.

Свойства непрерывных функций. Непрерывность сложной функции.

Теорема 1. Пусть функции f(x) и g(x) непрерывны в точке х₀. Тогда функции f(x)±g(x), f(x)g(x) и (если g(x₀)¹0) непрерывны в точке х₀.

Доказательство.

Пусть f(x) и g(x) непрерывны в точке x₀. Это значит, что . Но тогда, по свойствам пределов

Последнее свойство верно, если . <

Пусть y=f(x), но x, в свою очередь, является функцией некоторого аргумента t: x=j(t). Тогда комбинация y=f(j(t)) называется сложной функцией, или суперпозицией функций f(x) и j(t).

Примеры:

а) y=sin(x), x=e^t Þ y=sin(e^t)

б) y= e^x , x=sin(t) Þ y= e^sin(t)

Доказательство.

Докажем теорему только для супремума.

1. Построение последовательности. По первой теореме Вейерштрасса, f(x) ограничена сверху на [a, b], то есть

По свойствам супремума, к нему можно подойти сколь угодно близко. Поэтому . Беря n=1,2,3,… получим последовательность {x₁, x₂, x₃,…} такую, что .

2. Выделение подпоследовательности. Так как n a£x_n£b, то по лемме Больцано-Вейерштрасса, из последовательности {x_n} можно выделить сходящуюся подпоследовательность такую, что , причем сÎ[a, b] в силу его замкнутости.

3. Достижение супремума. Для нашей подпоследовательности верно условие

.

Переходя к пределу k®¥, получим

.

Но , кроме того, в силу непрерывности f(x), . В результате получим, что M£f(c)£M, то есть f(c)=M и супремум f(x) достигается в точке с. <

Монотонные функции.

Докажем теперь две теоремы, касающиеся непрерывности монотонных функций.

Теорема 1. Пусть f(x) определена и монотонна на замкнутом отрезке [a, b]. Тогда она может иметь на этом отрезке только разрывы I рода (скачки).

Доказательство.

Пусть, для определенности, f(x) монотонно возрастает.

Возьмем какую-то точку x0 Î[a, b]. Пусть мы приближаемся к точке х0 слева (см. рис.). Тогда при этом значения функции f(x) будут монотонно возрастать. Но они будут ограничены сверху, например, величиной f(x0). Поэтому, по теореме о пределе монотонно возрастающей функции будет существовать конечный . При движении к х0 справа значения f(x) будут монотонно убывать, но будут ограничены снизу величиной f(x0). Поэтому снова существует конечный .

Если f(x₀+0) = f(x₀-0), то f(x) будет непрерывна в точке х₀, если же f(x₀+0)>f(x₀-0), то у f(x) в точке х₀ будет разрыв I рода. <

Определение. Говорят, что значения функции f(x), определенной на <a, b>, заполняют некоторый отрезок <c, d> сплошь, если

.

Теорема 2. Для того, чтобы монотонная функция f(x) была непрерывной на [a, b], необходимо и достаточно, чтобы ее значения заполняли отрезок [f(a), f(b)] сплошь.

Доказательство.

Пусть, для определенности, f(x) монотонно возрастает.

1. Достаточность. Пусть f(x) непрерывна на [a, b]. Тогда , . Согласно второй теореме Больцано-Коши,

.

Поэтому отрезок [f(a), f(b)] заполнен сплошь.

2. Необходимость. При доказательстве необходимости в этой теореме используется достаточно редко применяемый прием. Он основан на следующем соотношении из алгебры логики

.

Вместо того, чтобы доказывать, что доказывают, что .

В нашем случае это выглядит так: вместо того, чтобы доказывать следование «функция заполняет некоторый отрезок сплошь Þ она непрерывна», доказывают следование «функция не непрерывна Þ ее значения не заполняют отрезок сплошь».

Итак: пусть f(x) не является непрерывной на [a, b]. Тогда она на [a, b] может иметь только разрывы I рода. Пусть х₀ – координата такого разрыва. Возможные варианты поведения графика f(x) изображены на рисунках.

Из них видно, что в этом случае отрезок [f(a), f(b)] заполнен не сплошь. <

Показательная функция.

.

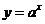Мы не будем давать строгого определения показательной функции, так как изложенного выше материала для этого недостаточно. Будут изучены лишь свойства этой функции.

Рассмотрим подробно случай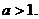

1. Основное свойство показательной функции имеет вид

.

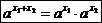Иногда именно это свойство принимается в качестве определения показательной функции, так как можно показать, что среди непрерывных функций показательная функция – единственная функция, удовлетворяющая свойству 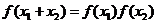. Следствием этого свойства является следующее свойство показательной функции: .

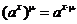2. Если 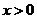, то 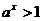; при любых значениях х .

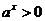3. При 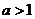функция 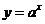строго монотонно возрастает.

Пусть 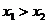. Тогда 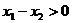и мы имеем

,

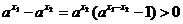так как 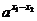>1. Следовательно .

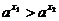4. .

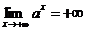Представим а в виде а =1 + l. Тогда l>0.

Пусть х = n где n - целое положительное число. Тогда, используя формулу бинома Ньютона, получим

.

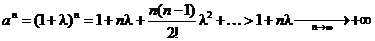Следовательно .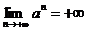

Пусть теперь х > 0 и n = [x] есть целая часть х. Тогда 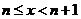; при х®+¥ также и n®+¥ и мы имеем

.

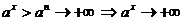5. .

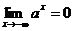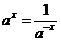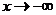
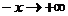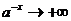Действительно, . При , и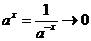

6 . 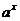непрерывна при любом х.

Пусть 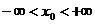. Возьмем любое 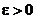и найдем такое целое число n, чтобы выполнялось соотношение

.

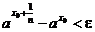Можно ли это сделать?

Имеем следующую цепочку неравенств.

;

;

;

;

.

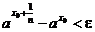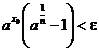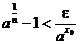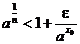Поэтому, если мы добьемся выполнения неравенства

,

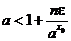то предыдущее неравенство будет и подавно выполнено. Но последнее неравенство верно при

,

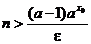так что искомое n всегда существует.

Но тогда, при х, удовлетворяющем неравенству

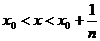
имеем

,

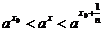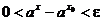
и функция a^x непрерывна в точке х₀ справа.

Аналогично доказывается, что функция a^x непрерывна в точке х₀ слева, и поэтому функция a^x непрерывна в точке х₀.

7. Значения функции a^x заполняют сплошь отрезок (0, +¥).

Случай 0 < a < 1 рассматривается аналогично. В этом случае функция a^x строго монотонно убывает, непрерывна при любых х, и 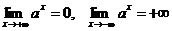. Ее значения также заполняют сплошь отрезок (0, +¥).

Вид графика показательной функции при а > 1 и при 0 < a < 1 приведен на рисунке.

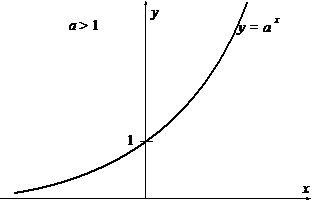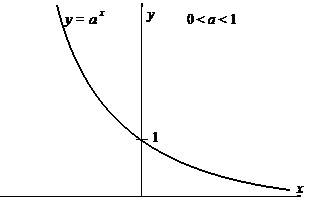Математики особенно «любят» функцию 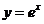, то есть показательную функцию при а=е. Ее называют экспоненциальной функцией, или просто экспонентой. Для нее часто используют обозначение .

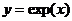Гиперболические функции.

С функцией e^x тесно связаны функции, получившие название гиперболических. К ним относятся:

гиперболический синус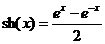

гиперболический косинус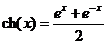

гиперболический тангенс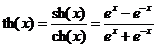

Рассмотрим коротко свойства этих функций.

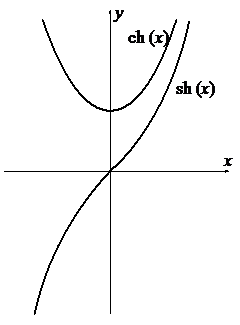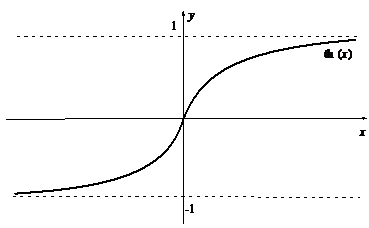1. Область определения этих функций -¥<x<+¥

2. sh(-x)= –sh(x), th(-x)= –th(x), ch(-x)= ch(x), то есть sh(x) и th(x) являются нечетными функциями, а ch(x) – четной функцией. Графики их изображены на рисунках.

3. sh(х), ch(x) и th(x) непрерывны для всех х.

4. sh(x) и th(x) монотонно возрастают.

5. Выведем основные формулы, касающиеся этих функций, и очень напоминающие формулы тригонометрии.

а) ch²(x) - sh²(x)=1.

Действительно,

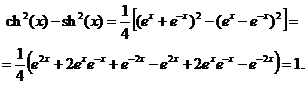
б)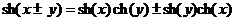

Вывод этой формулы надо вести с правой части. Имеем:

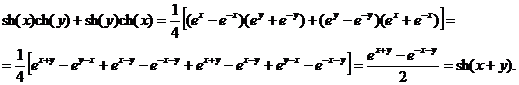
в) .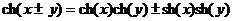

Аналогично имеем:

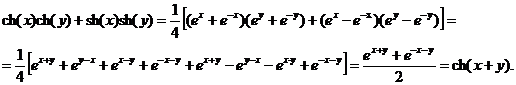
Аналогично выводятся формулы и для комбинации 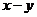. Можно вывести и много других формул, аналогичных формулам геометрии.

Логарифмическая функция

Функция, обратная a^x, называется логарифмической функцией, и обозначается log_ax. Ее свойства получаются как следствия свойств функции a^x

а) а > 1.

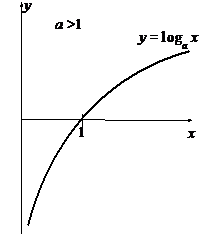1. Так как. значения axÎ(0; +¥), то logax определена для 0<x<+¥. 2. Так как ax строго монотонно возрастает, то logax тоже строго монотонно возрастает. 3. Так как ax непрерывна, то и logax тоже непрерывна. 4. 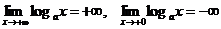. 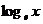называется натуральным логарифмом и обозначается ln(x).

б) 0 < а < 1

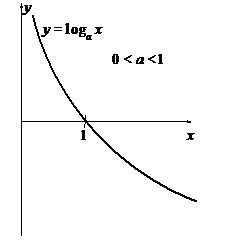1. log ax определена для 0<x<+¥. 2. log ax строго монотонно убывает. 3. log ax непрерывна. 4. .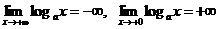

Основное свойство логарифмической функции имеет вид:

.

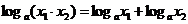Докажем это свойство. Действительно, используя тот факт, что логарифмическая функция является функцией, обратной показательной, мы можем записать

, .

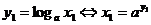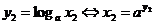Но тогда, используя основное свойство показательной функции, получаем

.

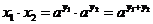Снова используя тот факт, что логарифмическая функция является функцией, обратной показательной, получаем

,

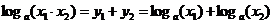что и требовалось доказать.

Можно показать, что log_ax – единственная непрерывная функция, удовлетворяющая свойству .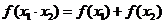

Другие важные формулы, касающиеся логарифмической функции

а) ;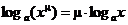

б) .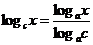

Степенная функция

Функция 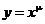где m – произвольное вещественное число, называется степенной функцией. В общем случае она определяется следующим образом:

.

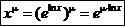Из этого определения следуют и все ее свойства.

1. Так как функция 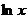определена для 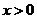, то и степенная функция в общем случае определена лишь для 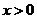(хотя для случая, когда m - целое число, ее определяют и для отрицательных значений х).

2. 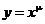- непрерывная функция, как суперпозиция непрерывных функций.

3. Монотонность.

Имеем для :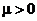

,

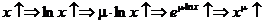то есть при 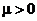степенная функция является строго монотонно возрастающей функцией.

Аналогично, для ,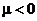

,

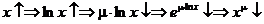то есть при 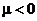степенная функция является строго монотонно убывающей функцией.

4. Поведение п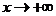ри и при .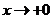

Имеем для :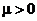

,

.

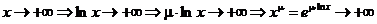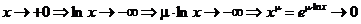Аналогично, для ,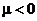

,

.

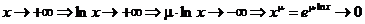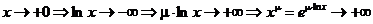Тригонометрические функции

Так как эти функции подробно изучаются в школе, то напоминать их свойства мы не будем. Рассмотрим лишь вопрос об их непрерывности. Основным здесь для нас будет неравенство 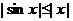, которое мы примем без доказательства.

Функция sin x .

Имеем

,

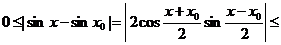
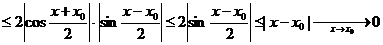так что sin x₀ непрерывен при любом х₀.

Функция cos x.

Аналогично предыдущему, имеем

,

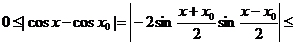
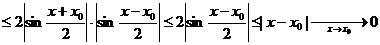так что cos x₀ непрерывен при любом х₀.

Функция tg x.

Так как функции sin(x) и cos(x) непрерывны для всех x, то 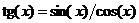имеет разрывы второго рода в точках, где cos(x)=0, то есть в точках 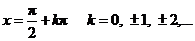При остальных значениях аргумента tg(x) непрерывен.

Замечательные пределы.

Рассмотрим примеры на вычисление пределов функции из числа тех, которые получили в математике название «замечательных».

1. .

Рассмотри окружность радиуса и некоторый угол с вершиной в центре окружности. В точке проведем касательную к окружности. Тогда, как видно из рисунка, . Поэтому . Так как высота равна , а , то , то есть при . Деля все части этого неравенства на ,

и «переворачивая» его, получим

.

Перейдем в этих неравенствах к проделу х®0. Тогда получим

.

Но мы только что показали, что cos x - непрерывная функция. Поэтому и, по теореме о «двух милиционерах», отсюда следует, что

.

Это соотношение можно записать и так:

,

что используется при вычислении пределов чтобы избавиться от функции sin (…).

Рассмотрим еще один полезный предел. Имеем:

,

который можно записать так:

.

Это соотношение также используется при вычислении пределов чтобы избавиться от функции cos (…).

2. .

Этот предел является обобщением предела . Выведем его.

а) Пусть есть последовательность положительных целых чисел, такая, что и . Но тогда последовательность есть подпоследовательность последовательности и поэтому

.

б) Пусть есть любая монотонно возрастающая последовательность положительных вещественных чисел, такая, что , и пусть есть целая часть числа x_k. Тогда "k и мы имеем следующую цепочку неравенств:

;

.

Но тогда

,

,

откуда, по теореме «о двух милиционерах» следует, что

.

Так как этот предел не зависит от вида последовательности , то

.

в) Пусть теперь х®-¥. Тогда и, так как, , имеем

,

и поэтому, учитывая, что , получаем

,

Объединяя вместе две эти формулы, можем окончательно записать

.

Рассмотрим еще некоторые пределы, которые полезно знать.

3. В только что полученном пределе сделаем «замену переменных» . Тогда при х®±¥ z®0 и мы получаем

.

4. Вспомним, что log_a – непрерывная функция. Логарифмируя предыдущее равенство, получим:

.

Итак,

.

В частности,

.

Это соотношение можно записать и в таком виде

.

5. В предыдущем соотношении сделаем снова замену переменных . Тогда при получаем

.

Переворачивая это соотношение, получим

.

В частности,

.

Это соотношение можно записать и в таком виде

.

6. Докажем, что

.

Для этого положим . Тогда при x®0 y®0. Далее , и логарифмируя это равенство, получим

.

Далее имеем

,

так как оба написанных предела равны 1.

Этот предел можно записать и в такой форме

.

7. Докажем, что при a > 1 и при m > 0

.

а) Докажем сначала, что при a > 1 . Действительно, обозначим a=1+l, l>0. Пользуясь формулами бинома Ньютона, получим

.

Поэтому , и при , то есть .

б) Возьмем произвольное x®+¥ и обозначим n = [x], то есть n - целая часть от x. Тогда n £ x £ n+1 и получаем

,

так что . Поэтому .

в) Наконец, при произвольном m > 0 имеем

.

8. Докажем, что при m > 0 и a > 1

.

Действительно, делая замену переменных log_a(x)=y, x=a^y, получим, что при x®+¥, y®+¥ и

.

9. Докажем, что при m > 0 и a > 1

.

Действительно, делая замену переменных , получим

.

Степенные неопределенности.

Рассмотрим теперь предел вида . Так как , то, пользуясь непрерывностью функции e^x, можно записать

,

и проблема вычисления искомого предела сводится к вычислению предела .

Это можно сформулировать в виде следующего правила: для вычисления предела выражения вида надо это выражение сначала прологарифмировать.

Какие же неопределенности могут иметь здесь место? Так как приходится вычислять , а здесь возможна только неопределенность типа , то возможны следующие варианты.

1. . Последнее означает, что и поэтому говорят, что мы имеем дело с неопределенностью типа .

2. . Последнее означает, что , и поэтому говорят, что мы имеем дело с неопределенностью типа 0⁰.

3. . Последнее означает, что и поэтому говорят, что мы имеем дело с неопределенностью типа 1^¥.

В последнем случае можно дать более простую формулу для вычисления величины с. . Мы имеем следующую цепочку преобразований

,

так как после замены переменных , получим:

.

Эта формула гораздо проще для вычислений.

Определения.

Определение 1. Функция f(x) называется непрерывной в точке х₀, если .

Дадим несколько расшифровок этого важнейшего определения.

а) Вспоминая понятие предела, запишем непрерывность f(x) в точке х₀ в виде

.

б) Так как , то непрерывность в точке х₀ можно записать в виде

.

Отсюда следует важнейшее свойство непрерывной функции: для непрерывной функции можно переставлять местами знак функции и знак предельного перехода

в) Обозначим Dx=x-x₀ (приращение аргумента) и Df=f(x) - f(x₀) (приращение функции). Тогда непрерывность в точке х₀ означает, что , то есть бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции.

Ведем обозначения:

,

если эти пределы существуют.

Определение 2. Функция f(x) называется непрерывной в точке х₀ слева (справа) если f(x₀)=f(x₀ – 0) (f(x₀)=f(x₀+0)). Очевидно, что непрерывность в точке х₀ означает непрерывность слева и справа одновременно.

Определение 3. Функция f(x) называется непрерывной на некотором множестве Х, если она непрерывна в каждой точке этого множества, то есть если

Обратите внимание, где стоит квантор , это важно.

Определение. Если функция f(x) не является непрерывной в точке х₀, то говорят, что в точке х₀ функция f(x) имеет разрыв.

Типы разрывов.

А.Пусть существуют конечные f(x0-0) и f(x0+0), они равны друг другу, но не равны значению функции в точке х0, то есть выполнено условие f(x0-0) = f(x0+0) ≠ f(x0), то говорят, что в точке х0 функция f(x) имеет устранимый разрыв. Действительно, достаточно изменить значение функции в точке х0 и разрыв исчезнет. Вид графика функции в этом случае приведен на рисунке.

В. Пусть существуют конечные f(x₀-0) и f(x₀+0), но они не равны друг другу . Тогда говорят, что в точке х₀ функция f(x) имеет разрыв I рода или скачок.

График функции f(x) в окрестности точки х₀ имеет в этом случае примерно такой вид:

Величина |f(x₀+0)-f(x₀-0)| называется величиной скачка функции f(x) в точке х₀.

В. Если хотя бы один из пределов или бесконечен или не существует, то говорят, что в точке х₀ функция f(x) имеет разрыв второго рода.

Виды графика функции f(x) в окрестности точки х₀ в этом случае гораздо разнообразнее. Некоторые возможные варианты приведены ниже.

, ,

, ,

,	; и не существуют.

Свойства непрерывных функций. Непрерывность сложной функции.

Теорема 1. Пусть функции f(x) и g(x) непрерывны в точке х₀. Тогда функции f(x)±g(x), f(x)g(x) и (если g(x₀)¹0) непрерывны в точке х₀.

<