Аппроксимация переходной характеристики объекта по управляющему каналу

Согласно заданным в таблице1 экспериментальным точкам строится экспериментальная характеристика переходного процесса. Исследуемый объект – двухканальный (канал: u-y и канал: f-y) по каналу регулирования (u-y) является объектом с самовыравниванием. Объекты с самовыравниванием аппроксимируют передаточными функциями с введением звена запаздывания.

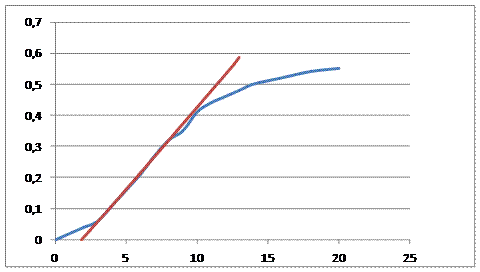
Рис. 2. Переходная характеристика по управляющему каналу

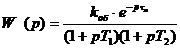, (1.1)

При Т₁=Т₂ и Т₁≠Т₂

где:

К_об – коэффициент передачи;

t - время запаздывания;

Т_о – постоянная времени.

Для определения параметров объекта по управляющему каналу проведём касательную к экспериментальной переходной характеристике в точке перегиба, которая имеет координатами (t_п; h(t_п)). Далее определяем параметры передаточной функции по управляющему каналу:

К_об = h_уст = 0,55; t_о = 1,85 с; Т_о = 10,55 с; h(t_п) = 0,14; t_п = 4,6 с

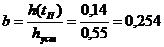
Аппроксимацию переходной характеристики объекта по управляющему каналу будем осуществлять с помощью 4,5,6 моделей. Наилучшей аппроксимирующей моделью будет считать ту, у которой ошибка аппроксимации будет наименьшей.

1. Если на графике переходной характеристики (рис. 2) просматривается характерный для s - образных кривых прямолинейный участок, то хорошую аппроксимацию дает модель 4, т.е. передаточная функция с одинаковыми постоянными времени, которая имеет вид[1]:

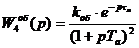(1.2)

Параметры модели определяем по методу Лукаса:

где, ;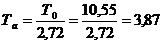

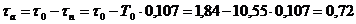
Таким образом, получили четвертую математическую модель ОУ:

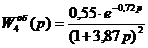
2. Если истинная кривая (рис. 2) медленно приближается к установившемуся значению и координата h_a ≤:0,8 k_об, то предпочтительней передаточная функция (1.3), модель 5,[1]:

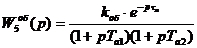(1.3)

Существуют разные подходы к определению параметров. Часто принимают условие T_a1/T_a2 = 0,5 , тогда подход следующий, берется координата 0,63 k_об и определяется время t₁. Затем из t₁ вычитаем время чистого запаздывания .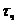

t₁=8,5 с 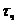= 0,8 с

t₂= t₁ - 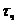= 8,5 – 0,8 = 7,7 c T_a2 = 0,64*t₂= 0,64*7,7 = 4,928 c

T_a1 =0,5 * T_a2 =0,5*4,928 = 2,464 c 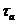= =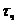0,8 c

Подставляя полученные параметры в (1.3) получим:

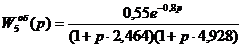
Модель 5 считается наилучшей если h(0,5*t₂) ≥ 0,3*k_об (*)

где, h(0,5*t₂) = 0,11 0,3*k_об = 0,165

следовательно h(0,5*t₂) ≤ 0,3*k_об - условие не выполняется.

3. Если (*) не выполняется, то предпочтительней модель 6, передаточная функция которой представлена выражением (1.4),[3]]:

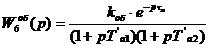(1.4)

Параметры определяются по методу Роточа с использованием номограмм[3]. Задача математического описания в этом случае заключается в поиске таких Т^’_а1, Т^’_а2 и 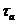, при которых кривая (1.4) максимально приближается к истинной экспериментальной кривой. Записывая аналитические выражения критерия приближения, получаем уравнения для выбора этих параметров. Для упрощения расчётов, в литературе предложена номограмма:

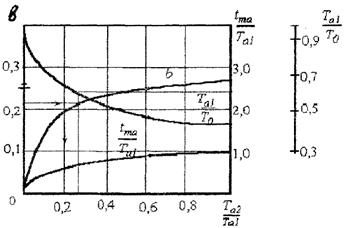
Рис. 3. Номограмма для определения параметров передаточных функций

По номограмме (рис.3.) можно найти Т^’_а1, Т^’_а2 по известным 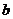и 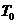. По известному значению 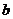находим значение 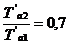, после чего определяем 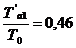, 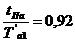и, следовательно:

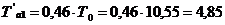
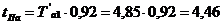
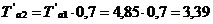
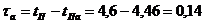
Подставляем рассчитанные значения в формулу (1.4):

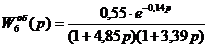
Далее с помощью ППП «MATLAB» на ЭВМ строим переходные процессы полученных функций, рис 4.

Вычислим погрешности аппроксимации полученных передаточных функций по интегральному критерию по формуле:

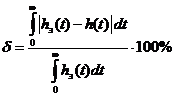
где:

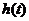- аппроксимирующая переходная характеристика;

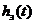- заданная переходная характеристика.

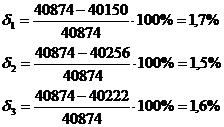
Выбираем передаточную функцию, имеющую наименьшую погрешность аппроксимации:

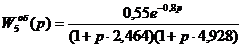(1.5)

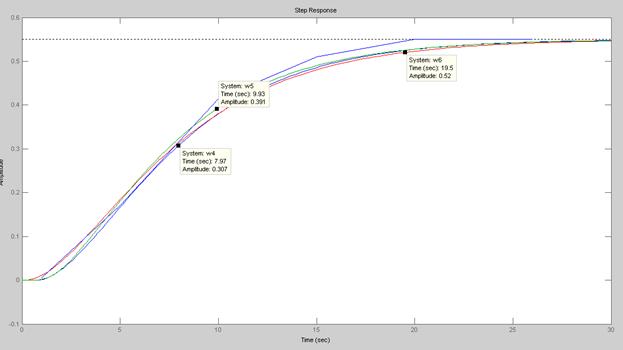
Рис. 4 Переходные характеристики моделей объекта управления по управляющему каналу и заданная экспериментально переходная характеристика по управляющему каналу.

1 -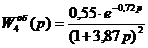

2 -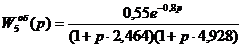

3 -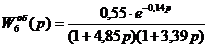

4 - заданная экспериментально переходная характеристика по управляющему каналу