В зависимости от расположения значения линейной формы

Анализ предельной производительности факторов позволяет обнаружить, что максимально возможная производительность фактора достигается в тех точках, в которых плотность имеет наибольшее значение. Интересно, что именно в этих точках ситуация бинарного выбора обладает самым высоким уровнем неопределенности. Это становится совершенно очевидным для логит-модели, если вспомнить о выражении для плотности и предельную производительность ее -го фактора записать в виде

. (3.14)

Максимальное значение первой составляющей, которая в данном выражении представлена произведением вероятностей, достигается при , т.е. когда имеет место самый высокий уровень неопределенности.

Вторая составляющая менее интересна для анализа. Она равна постоянной величине и в основном играет роль мультипликатора, усиливающего или снижающего вклад первой в предельную производительность. Геометрически (рис. 3.1) при увеличении на единицу коэффициент определяет ширину прямоугольника с высотой , на величину площади которого изменяется вероятность бинарного выбора в условиях, описываемых вектором .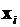

Так как события бинарного выбора несовместны, то при рассмотрении результатов предельного анализа нужно помнить, что увеличение вероятности возможного появления одного из событий влечет за собой уменьшение на ту же самую величину вероятности возможного появления альтернативного события. Поэтому, если из двух вероятностей увеличивается при изменении та, которая имеет большее значение, то неопределенность выбора снижается, если та, которая имеет меньшее значение, то неопределенность выбора увеличивается.

Переходя к интерпретации результатов моделирования экспертных предпочтений, прежде всего попытаемся понять смысл расчетных значений

. (3.15)

С одной стороны это вероятность возможного появления события, состоящего в том, что 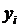примет значение равное 1, а с другой это характеристика оставшейся в предпочтениях эксперта неопределенности. Действительно с ее помощью можно вычислить энтропию

, (3.16)

которая характеризует уровень неопределенности бинарного выбора, сохраняемый в точке 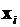после экспертного опроса.

Предельная производительность фактора, изменяя вероятность выбора, естественно, изменяет и энтропию ситуации, в которой осуществляется выбор. Причем, как упоминалось выше, рост вероятности в одних случаях снижает энтропию, а в других приводит к ее увеличению. Фактически это означает, что для эксперта более важной является информация о ситуации, в которой он будет принимать решение, а не информация о возможном изменении ситуации.

Ситуацию с максимальной энтропией можно понимать как равновесную, смысл которой в том, что эксперт не располагает информацией, позволяющей одну альтернативу предпочесть другой. Естественно, что именно в этой ситуации любая информация, позволяющая изменить степень предпочтения эксперта, ценится дороже, чем та же самая информация, но в условиях, когда уже сформированы убедительные предпочтения.

На основе результатов анализа предельных производительностей легко выстраивается процедура ранжирования факторов по степени их влияния на вероятность появления интересующего нас события (на изменение уровня неопределенности). В основе процедуры лежит простое соображение. Так как первая составляющая (плотность вероятности) одинакова для всех факторов, то порядок значимости факторов следует определять по абсолютной величине коэффициентов бинарной регрессии. Если вспомнить, что в случае линейной модели ранжирование факторов по величине соответствующих коэффициентов регрессии некорректно, то вывод следует признать неожиданным.

Таким образом, предельный анализ модели экспертных предпочтений позволяет оценить влияние факторов на уровень неопределенности в каждой ситуации бинарного выбора, а также упорядочить все факторы по степени их влияния на выбор в любой из рассмотренных ситуаций.