Уточнение корней уравнения в окрестности начального приближения. Сканирование с переменным шагом
В отличие от уточнения корня на доверительном отрезке, в данном случае исходными данными помимо функции f(x) и необходимой точности решения e является только одна начальная приближенная точка x0, достаточно близкая к искомому корню уравнения x*. Требуется построить последовательность приближенных решений {xi} (i=1,2,...), сходящуюся к точному корню уравнения x*, который будет ближайшим к начальному приближению x0. Корень x* будет ближайшим к x0 сверху, если функция f(x)>0 и убывает в точке x0, и, наоборот, если функция f(x)<0 и возрастает в точке x0. В других случаях искомый корень x* будет ближайшим к x0 снизу.
Наиболее распространенными методами уточнения корней в окрестности начального приближения являются:
1) сканирование с переменным шагом,
2) метод простой итерации,
3) метод Ньютона (метод касательных).
У метода 1) сканирования с переменным шагом точность определения корня задается длиной итогового доверительного отрезка e. У методов
простой итерации (2) и касательных (3) условием завершение итерационного процесса является, как и в методе хорд, уменьшение величины приращения значения приближенных значений корня до заданной предельной величины e: | xi - xi - 1| < e.
Методы 1) сканирования с переменным шагом и 2) простой итерации имеют нулевой порядок - в них используется только расчет значений целевой функции f(x). Метод касательных 3) имеет первый порядок, поскольку использует также первую производную f¢ (x).
8.5.1. Сканирование с переменным шагом
Поиск корня в окрестностиприближенной точки x0 по методусканирования с переменным шагом заключается в начальном просмотре (сканировании на первой итерации) значений функции f(x) в направлении точного значения корня x* с крупным шагом h1 в результате которого определяется доверительный отрезок [a1,b1] длины h1, внутри которого находится x*. Затем шаг сканирования уменьшается в заранее заданное число раз k (k>1) и просмотр значений функции f(x) производится, начиная с последней точки, в обратном направлении (h2:= -h1/k) с определением доверительного отрезка [a2,b2] сокращенной длины h2. Процесс уменьшения и смены направления сканирования (hi:= -hi-1/k) продолжается до тех пор, пока корень x* не будет локализован на доверительном отрезке длины (bi - ai) = hi, не превышающей заданной точности e. Длина шага на последней итерации равна модулю ïhiï= ïh0ï/ki-1.
Начальное значение шага сканирования h1 и коэффициент сокращения шага k для максимального сокращения вычислений функции f(x) должны быть приняты по возможности достаточно большими, но, в то же время, таким, чтобы не допустить при сканировании пропуска рядом расположенной пары корней функции или слияния трех близко расположенных корней в одно решение. Очевидно, в общем случае величины h1 и k должны выбираться с учетом особенностей функции f(x) и необходимой точности решения e.
После задания h1 и k выполнение метода не учитывает особенности функции f(x). Как и в методе половинного деления, при случайном попадании в корень имеется возможность неправильного определения знака функции f(x) в очередном узле при малом значении ïf(x)ï и потери соответствующего корня. Поэтому для корректной работы метода во всех случаях необходимо учитывать точность ef расчета функции f(x) и производить проверку ïf(xi)ï< ef, как и в методе половинного деления.
С учетом вышесказанного полная постановка задачи уточнения корня по методусканированияс переменным шагом должна содержать следующие исходные данные:
1) начальноеприближение корня x0,
2) необходимую точность определения корня e,
3) точность ef расчета функции f(x),
4) начальное значение шага сканирования h1,
5) коэффициент сокращения шага k.
Зависимость ïhiï= ïh1ï/ki-1 ≤ e может быть использована для задания связи между параметрами задачи (h1,k,i). Например, при заданном коэффициенте k и числе итераций i длину начального шага ïh1ïна первой итерации можно задать равной ïh1ï=e×ki-1.
Корректная расширенная постановка задачи с учетом возможного попадания в корень означает численное определение: 1) либо нового итогового доверительного отрезка[a,b] длины, не превышающей e (8.5а), 2) либоприближенного значения корня xпр, у которого ïf(xi)ï< ef (8.5б).
С учетом расширенной постановки задачи уточнения корня (8.5а)-(8.5б) численный алгоритм ее решения на каждой итерации i при известном последнем расчетном узле сi-1 - одной из крайних точек доверительного отрезка [ai-1,bi-1] и значении шага hi-1 (ïhi-1ï>e) на предыдущей итерации (i -1) должен вначале содержать расчет длины и направления шага hi-1 на текущей итерации i: hi:= -hi-1/k. Затем производится расчет значений функции в узлах вида di,j = сi-1 + j × hi: (j = 1,2,...), в каждом узле di,j производятся проверки условий:
а) ïf(di,j)ï≤ ef - если оно выполнено, то имеет место попадание в корень, di,j принимаем в качестве его искомого уточненного значения и выходим из алгоритма,
б) иначе проверяем условие постоянства знака функции на последнем расчетном шаге f(di,j)×f(di,(j-1)) >0 - если оно выполнено, продолжаем проход по узлам,
в) иначе (f(di,j)×f(di,(j-1))<0) проверяем условие окончания работы алгоритма hi ≤ e, если оно выполнено, отрезок [di,(j-1), dij] принимаем в качестве искомого итогового доверительного отрезка и выходим из алгоритма, иначе принимаем сi:= di,j и переходим к выполнению следующей итерации.
В качестве искомого решения принимаем последний доверительный отрезок [di,(j-1), dij] или приближенное узловое значение di,j, если произошло попадание в корень.
При учете погрешности расчета значений функции метод сходится всегда, поскольку после выполнения каждой итерации i точное значение корня x* удерживается на доверительном отрезке [ai,bi] уменьшающейся длины. Скорость сходимости невысока из-за переборного характера применяемого алгоритма поиска уточнения.
Пример 1. Уточнить по методу сканирования с переменным шагом корень уравнения f(x) = x3 - 6х + 2 = 0 из примера 1 п.8.2 с точностью e = 0,01 в окрестности приближенного значения x0 = 3. Точность вычисления функции ef = 0,0001.
Решение. Примем коэффициент сокращения шага k=10, число итераций i=2. Тогда из зависимости ïhiï= ïh1ï/ki ≤ e получим, что длина начального шага ïh1ïна первой итерации может быть принята равной ïh1ï=e×ki-1 = 0,01×10 = 0,1.
Так как f(3) = 11 > 0, то знак h0 должен быть выбран в направлении убывания функции (приближения ее к нулю). Пробные расчеты дают: f(3 - 0,1) = (2,9)3 - 6(2,9) + 2 = 8,989 <11 = f(3), f(3 + 0,1) = (3,1)3 - 6(3,1) + 2 = 13,191>11. Поэтому задаем: h1 = - 0,1.
Итерация 1. С учетом найденного значения f(2,9) = 8,989 >0 продолжаем вычисления значений функции до получения отрицательной величины (или попадания в корень с точностью ef):
f(2,8) = 7,152>0; f(2,7) = 5,483>0; f(2,6) = 3,976>0; f(2,5) = 2,625>0; f(2,4)=1,424>0; f(2,3) = 0,367>0; f(2,2) = -0,552<0.
Так как во всех точках ïf(di,j)ï >ef и ïh1ï = 0,1>e, то принимаем сi:=2,2и переходим к следующей итерации.
Итерация 2. Принимаем: h2 = - h1/10 = 0,01. С учетом f(2,2)<0 вычисляем значения функции с шагом h2 до получения положительной величины (или попадания в корень с точностью ef):
f(2,21) = -0,4661<0; f(2,22)= -0,379>0; f(2,23)= -0,2904<0; f(2,24)= -0,2006<0; f(2,25) = -0,1094<0; f(2,26) = -0,0168<0; f(2,27) = 0,0771>0.
Так как во всех точках ïf(di,j)ï >ef , то после смены знака функции проверяем длину полученного доверительного интервала. Так как ïh1ï = 0,01=e, то в качестве решения принимаем последний доверительный отрезок [2,26; 2,27].
Как видно из примера, метод не оптимален по числу вычислений функции - на поиск решения потрачено: 2 пробных расчета, 7 расчетов на итерации 1 и 7 расчетов на итерации 2 - всего 16 расчетов значения функции, что значительно превышает даже число расчетов в методе половинного деления.
Достоинствами метода является его простота и гарантированная сходимость к искомому корню для любой непрерывной функции, в том числе недифференцируемой на начальном доверительном отрезке.
Вопросы для проверки знаний.
1. Чем отличается уточнение корня в окрестности приближенной точки от уточнения на доверительном отрезке ?
2. Какие методы уточнения корней в окрестности начального приближения являются наиболее употребительными ?
3. Как задают точность решения в методах уточнения корней в окрестности начального приближения ?
4. Какой порядок имеют методы уточнения корней в окрестности начального приближения ?
5. В чем заключается основная идея уточнения корня в окрестности начального приближения при помощи метода сканирования с переменным шагом ?
6. Почему при корректной реализации метода сканирования с переменным шагом необходимо учитывать возможность попадания в корень?
7. Какой полный набор исходных данных должна содержать полная постановка задачи уточнения корня в окрестности начального приближения при помощи метода сканирования с переменным шагом ?
8. В каком виде может быть получено решение задачи уточнения корня в окрестности начального приближения при помощи метода сканирования с переменным шагом ?
9. Каковы достоинства и недостатки метода уточнения корня в окрестности начального приближения при помощи сканирования с переменным шагом ?
Практические задания.
1. Уточнить по методу сканирования с переменным шагом корень уравнения f(x) = x4 - х - 14 = 0 с точностью e = 0,2 на отрезке [1,5;3].
2.Отделить положительный корень уравнения f(x) = x3 - 0,2 x2 - 0,2 х - 1,2 = 0 и уточнить его с точностью e = 0,05.
Метод простой итерации
Допустим, необходимо уточнить корень уравнения f(x)=0 при заданном начальномприближении x0 и необходимой точности определения корня e. В методе простой итерации исходное уравнение приводят к специальному виду x=φ(x), (8.9)
который удобен для применения метода простой итерации.
Схема метода простой итерации при заданном начальном приближении x0 имеет вид:
xi=φ(xi-1), (i=1,2,…,). (8.10 а)
Условие завершения итерационного процесса:
|xk+1–xk|<ε. (8.10 б)
Достаточным условием сходимостиметода является следующее условие:
1) функция φ(x) имеет первую производную φ¢ (x) на всей области поиска W (конечной или бесконечной),
2) для первой производной на W выполняется условие ½φ¢ (x) ½£ q <1.
Справедливость условия вытекает из следующих оценок, в которых используется теорема Лагранжа о среднем:
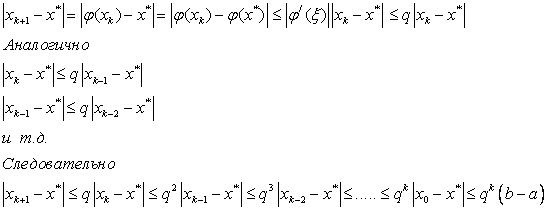
Так как 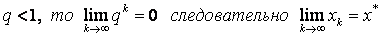 .
.
