Типовая последовательность действий при численном решении нелинейных уравнений. Локализация корней

Будем рассматривать уравнения, имеющие только изолированные корни, т.е. такие решения уравнения (8.1), для которых существует окрестность, не содержащая других корней.

Обычный алгоритм численного решения нелинейного уравнения содержит два этапа.

1. Локализация (отделение) корней заключается: 1) в определении отрезков на вещественной оси R, в пределах которых содержится единственный корень уравнения, их называют доверительными отрезками либо 2) определение значений аргумента функции, достаточно близких к искомому решению, их называют начальными приближениями корней.

2. Уточнение корней - вычисление приближенных значений корней на доверительных отрезках или в окрестности начальных приближений с заданной точностью.

Численное методы решений характеризуются наличием погрешностей как самих методов, так и погрешностей вычислений, поскольку промежуточные преобразования в них производятся не в формульном виде, а в числовом.

Рассмотрим локализацию корней. Определение доверительных отрезков, содержащих корни уравнения, основано на применении теоремы Больцано–Коши, доказываемой в курсе математического анализа, и ее следствии.

Теорема Больцано–Коши. Пусть на отрезке [a,b] дана непрерывная функция f(x), имеющая различающиеся значения в крайних точках: f(a) ¹ f(b). Тогда для любого значения СÎ[f(a), f(b)] существует такая точка с Î[a, b], в которой f(с)=С.

Следствие (Теорема о нуле непрерывной функции). Если непрерывная на отрезке [a,b] функция f(x) принимает в концах отрезка положительное и отрицательное значения (в этом случае f(a)f(b) < 0), то существует точка сÎ[a, b], в которой f(с)=0.

Замечание. Теорема о нуле непрерывной функции гарантирует существование корня уравнения f(x)=0 на отрезке [a, b], но не гарантирует его единственности.

8.2.1. Локализация корней при помощи сканирования с постоянным шагом

Простейшим методом определения доверительных отрезков, содержащих корни уравнения f(x)=0 с непрерывной функцией f(x) в левой части, является сканирование с постоянным шагом укрупненного отрезка числовой оси [A,B], содержащего все возможные корни уравнения. По данному методу вначале, исходя из допустимого числа N вычислений функции f(x) рассчитывается шаг h=(B-A)/N и производится расчет значений функции в точках x_i = A+ h×i. Среди всех анализируемых пар значений функции (f(x_i),f(x_i+1)) в качестве доверительных отрезков выбираются те, в которых выполняется условие:

f(x_i) × f(x_i+1) < 0. (8.3)

По следствию из теоремы Больцано–Коши условие (8.3.) гарантирует существование на отрезке [f(x_i),f(x_i+1)] хотя бы одного корня уравнения f(x)=0.

Надежность такого метода отделения корней уравнений зависит как от характера функции f(x), так и от выбранной величины шага h (числа N вычислений функции). Если корни функции лежат достаточно близко друг от друга, то при крупном шаге h могут возникнуть ситуации, когда:

1) при двух рядом лежащих корнях доверительный отрезок будет пропущен, поскольку f(x) на нем два раза поменяла свой знак,

2) при трех рядом лежащих корнях доверительный отрезок будет зафиксирован как содержащий только один корень, поэтому при уточнении будет найден с нужной точностью лишь один из трех корней, а два других будут потеряны.

Для предотвращения подобных ситуаций необходимо выбирать достаточно малые значения шага h. Также при поиске доверительных отрезков желательно знать возможное число корней уравнения.

Пример 1. Найти с использованием сканирования с постоянным шагом доверительные отрезки для уравнения с функцией f(x) = x³ - 6х + 2 = 0.

Решение. Алгебраическое уравнение третьей степени может иметь один или три вещественных корня. Предварительные оценки показывают, что f(-5) =-93 – отрицательное число, достаточно удаленное от оси х, f(5) =157 – положительное число, достаточно удаленное от оси х.

х	-5	-4	-3	-2	-1
знак f(x)	-	-	-	+	+	+	-	-	+	+	+

Принимая в качестве полной области поиска [A,B] отрезок [-5;5], сканируем его с шагом h=1. Результаты расчета знака функции даны в таблице 8.1.

Таблица 8.1. Знак функции в целочисленных точках отрезка [-5;5].

Ответ: анализ таблицы 8.1 показывает, что исследуемая функция имеет на вещественной оси три корня. Доверительные интервалы следующие: [-3,-2]; [0;1]; [2;3].

8.2.2. Метод локализации корней с использованием стационарных точек

Второй метод локализации корней на доверительных отрезках может быть реализован в том случае, когда у функции на заданной области (конечной или бесконечной) существует непрерывная первая производная f¢ (x) и для нее может быть разрешено уравнение f¢ (x) = 0 относительно х, такие точки называют стационарными. При этом прохождение через нуль может произойти только между крайними точками области определения функции и ее стационарными точками. Для каждой пары таких подряд стоящих точек достаточно проверить изменение знака функции. При этом, если крайняя точка области определения уходит в бесконечность и предел функции не существует, определяется знак бесконечности. Если изменение знака есть, то корень на данной части числовой оси есть, если нет – то корня не существует.

Пример 2. Найти с использованием второго метода (стационарных точек) доверительные отрезки для уравнения f(x) = x³ - 6х + 2 = 0 из примера 1.

Решение. Первая производная f¢ (x) = 3x² – 6. Приравнивая ее нулю, получаем уравнение для стационарных точек функции: 3x² – 6=0. Оно имеет два решения: x₁ = -(2)^0,5 и x₂=(2)^0,5. Функция рассматривается на всей числовой оси. Следовательно, для определения доверительных отрезков рассматриваем следующие упорядоченные по возрастанию значения аргумента: (-¥),(-(2)^0,5), ((2)^0,5),(+¥). Так как при х®-¥ f(x)®-¥, f(-(2)^0,5) = -2(2)^0,5+ 6(2)^0,5 + 2 > 0; f((2)^0,5) =2(2)^0,5 - 6(2)^0,5 + 2 < 0; при х®+¥ f(x)®+¥, то смена знака функции означает, что уравнение имеет 3 вещественных корня, для которых доверительными участками числовой оси являются: 1) (-¥,-(2)^0,5); 2) (-(2)^0,5,(2)^0,5); 3) ((2)^0,5, +¥).

Получаемые по второму методу доверительные участки числовой оси большого размера можно сократить, используя сканирование.

Одиночные начальные приближенные значения корней определяют, используя:

1) физический смысл задачи,

2) решения аналогичных задач,

3) графические методы решения,

4) учет специфики решаемого уравнения, его функции.

Например, если производится расчет текущего положения спутника, движущегося по околоземной орбите, то в качестве начального приближения принимают последнее известное его положение.

Вопросы для проверки знаний.

1. Какие этапы содержит алгоритм численного решения нелинейного уравнения ?

2. Какие используются два варианта локализации корней уравнений ?

3. Какие методы применяют для определения одиночных начальных приближенных значений корней ?

4. Сформулируйте теорему Больцано–Коши и ее следствие - теорему о нуле непрерывной функции.

5. Как и для чего выполняется сканирование с постоянным шагом ?

6. Какие возможны погрешности в определении доверительных отрезков в сканировании с постоянным шагом при использовании шага крупного размера ?

7. В чем заключается метод локализации корней с использованием стационарных точек ?

8. Как в методе локализации корней с использованием стационарных точек учитывается знак функции f(x) в исследуемой точке или на бесконечности (х®-¥или х®+¥), если в них значение f(x) стремится к бесконечности ?

Практическое задание.

1. Найти с использованием сканирования с постоянным шагом доверительные отрезки, содержащие корни уравнения f(x) = x⁴ - x³ - 20х + 25 = 0.

2. С использованием стационарных точек найти доверительные участки, содержащие корни уравнения f(x) =3x⁴ - 8x³ - 90x² - 200 = 0.

3. С использованием стационарных точек найти доверительные участки, содержащие корни уравнения f(x) =2sinx - x = 0.

8.3. Уточнение корней уравнения на доверительном отрезке.
Метод половинного деления

В простейшем случае уточнение корня на доверительном отрезке [a,b] с заданной точностью e означает задание абсолютной погрешности, с которой приближенное значение корня x_пр может отличаться от точного значения корня x*:

ï x* - x_прï≤ e . (8.4)

и численное определение нового итогового доверительного отрезка[a,b],на котором все точки x_прÎ[a,b] удовлетворяют условию (8.4).

Итерационное численное определение итогового доверительного отрезка[a,b] при простейшем варианте реализации методов уточнения заключается в последовательных вычислениях приближенных значений корня x₁, x₂,..., x_i, построении на каждом шаге i нового сокращенного доверительного отрезка [a_i,b_i] и проверке его длины. Если ïb_i - a_iï ≤ e, то доверительный отрезок требуемой длины e найден, вычисления завершаем. Иначе (при ïb_i - a_iï>e) переходим к новой итерации и продолжаем сокращать доверительный интервал.

Данная простейшая схема чаще всего срабатывает. Однако в реальных расчетах при поиске итогового доверительного отрезка[a,b] встречаются такие ситуации,когда для очередного приближенного значения x_i значение функции оказывается практически равным нулю: f(x_i) » 0. Данную ситуацию кратко назовем попаданием в корень, поскольку в этом случае значение x_i очень близко к искомому корню x*. При этом из-за погрешностей вычислений f(x_i) может возникнуть ошибка в знаке функции, из-за чего уже на следующей итерации может быть потерян искомый корень уравнения, т.е. будут строиться доверительные интервалы, не содержащие x*.

Для устранения возможной потери корней необходимо уже на этапе постановки задачи учесть погрешность вычисления функции и возможность попадания в корень.

Корректная (позволяющая всегда найти решение при возможном попадании в корень) постановка задачи уточнения на доверительном отрезке [a,b] с заданной точностью e и погрешностью вычисления функции e_f означает численное определение:

1) либо нового итогового доверительного отрезка[a,b] длины, не превышающей e :

(b - a) £ e (8.5а)

2) либоприближенного значения корня x_пр, у которого:

ïf(x_i)ï< e_f. (8.5б) С учетом новой постановки задачи уточнения корня (8.5а)-(8.5б) численный алгоритм ее решения на каждой итерации i при известном доверительном отрезке [a_i-1,b_i-1]из предыдущей итерации (i -1) должен включать следующие действия:

1) расчет очередного приближения х_i,

2) проверка условияïf(x_i)ï≤e_f - если оно выполнено, то найдено приближенное значение корня x_пр, для которого выполнено условие окончания расчета (8.5б), выход из алгоритма, иначе (ïf(x_i)ï> e_f) – продолжение расчетов;

3) сокращение доверительного отрезка, обозначим его [a_i,b_i], если ïb_i - a_iï ≤ e, то найден доверительный интервал требуемой длины e (выполнено условие окончания расчета (8.5а)), вычисления завершаем; иначе (ïb_i - a_iï>e) - переходим к новой итерации.

Основным требованием к итерационным методам решения уравнений является сходимость: предел последовательности получаемых значений неизвестного {x₁,x₂,x₃,...} должен существовать и быть равным искомому точному корню уравнения x*.

При наличии сходимости главным качественным показателем метода является скорость сходимости, которая определяется числом n вычислений функции f(x), необходимых для получения приближенного значения корня x_пр с заданной точностью e на исходном доверительном отрезке [a,b]. Таким образом, в общем случае n зависит от следующих факторов: 1) вида функции f(x), 2) длины доверительного отрезка (b - a), 3) точности решения e,т.е. в общем случае:

n = n(f(x),(b - a),e). (8.6)

Поскольку число необходимых расчетов функции f(x) возрастает с увеличением длины отрезка [a,b] и уменьшением точности e, то вместо двух данных факторов можно рассмотреть их отношение М=(b - a)/e, которое назовем масштабом задачи.

Наиболее распространенными методами уточнения корней на заданном доверительном отрезке являются следующие итерационные методы нулевого порядка, в которых используется только расчет значений целевой функции:

1) половинное деление,

2) метод хорд.

8.3.1. Метод половинного деления уточнения корней на доверительном отрезке

Допустим, для уравнения f(x)=0 заданы:

1) доверительный отрезок [a,b], на котором непрерывная функция f(x) меняет знак: f(a)× f(b) < 0,

2) точность e, с которой необходимо найти корень f(x),

3) допустимая погрешность вычисления значения функции e_f.

Необходимо найти приближенное значение корня x_пр с точностью e_f либо новый доверительный отрезок для него с точностью e .

Обозначим начальные значения границ отрезка через a₀ и b₀, на каждой очередной итерации i (=1,2,...) - через a_i и b_i.

Рассмотрим итерацию метода с номером i (=1,2,...). К началу ее известен доверительный отрезок [a_i-1,b_i-1] предыдущей итерации (i-1), на котором функция f(x) меняет знак: f(a_i-1)× f(b_i-1) < 0. На итерации i рассчитываем значение функции в средней точке отрезка [a_i-1,b_i-1], имеющей координаты: x_i = (a_i-1+b_i-1)/2. Для значения функции f(x_i) выполняем следующие проверки.

1. Если ïf(x_i)ï< e_f, то искомое приближенное значение корня считаем найденным (x_пр = x_i) ивыходим из алгоритма; иначе вычисления продолжаем;

2. Если выполнено условие f(a_i-1)× f(x_i) < 0, то это означает, что искомый корень содержится между точками a_i-1 и x_i, корректируем доверительный отрезок: a_i:=
a_i-1; b_i:=x_i;

иначе (f(a_i-1)× f(x_i) ³ 0) искомый корень лежит между точками x_i и b_i-1, корректируем доверительный отрезок: a_i:=x_i; b_i:= b_i-1.

3. Если ïb_i - a_iï ≤ e, то найден доверительный интервал требуемой длины e, вычисления завершаем; иначе (ïb_i - a_iï>e) - переходим к новой итерации (i +1).

При поиске корня с точностью e все промежуточные расчеты должны выполняться с более высокой точностью, для того, чтобы при округлении не "потерять" точный корень.

Сходимость метода. Поскольку метод на каждом шаге удерживает искомый точный корень x* на доверительном отрезке [a_i,b_i], длина которого который уменьшается в два раза по сравнению с предыдущим шагом, то метод всегда сходится к точному решению.

Скорость сходимости метода. Она не зависит от вида функции Поскольку на каждом шаге длина доверительного отрезка уменьшается ровно в два раза, то число шагов n равно числу делений числа (b-a) на 2, при котором результат окажется меньше либо равен e:(b-a)/2ⁿ ≤ e. Отсюда следует: 2ⁿ ³ (b-a)/e; n ³ log₂((b-a)/e);

n = n(f(x),(b - a),e) = ]log₂((b-a)/e)[ = ]log₂M[, (8.7)

где ]x[ - ближайшее целое сверху к значению x.

Пример 1. Уточнить по методу половинного деления корень уравнения f(x) = x³ - 6х + 2 = 0 из примера 1 п.8.2 с точностью e = 0,01 на отрезке [2;3].

Решение. Масштаб задачи равен: М=(b - a)/e =1/0,01 = 100. Следовательно, из (8.5) следует, что число необходимых итераций равно n = ]log₂(100)[ = 7. Из примера 1 п.8.2 следует, что f(2)<0; f(3)>0. Точность расчетов примем равной 0,0001. Рассмотрим выполнение итераций с номерами 1-7.

Итерация 1. х₁=(2+3)/2=2,5. f(2,5)= x³ - 6х + 2 = 15,625 - 15 + 2 = 2,625 > 0. ½f(2,5)½³ e_f, f(2,5)×f(2)<0, поэтому корень находится на отрезке [2;2,5], который принимаем в качестве нового доверительного. Длина его равна 0,5 >e.

Итерация 2. х₂=(2+2,5)/2=2,25. f(2,25)= x³ - 6х + 2 » 11,3906 - 13,5 + 2 = -0,1094<0. Так как f(2)×f(2,25)>0, то корень находится на отрезке [2,25;2,5], который принимаем в качестве нового доверительного. Длина его равна 0,25 >e.

Итерация 3. х₃=(2,25+2,5)/2=2,375. f(2,375)= x³ - 6х + 2 » 13,3965 - 14,25 + 2 = 1,1465>0. Так как f(2,25)×f(2,375)<0, то корень находится на отрезке [2,25;2,375], который принимаем в качестве нового доверительного. Длина его равна 0,125 >e.

Итерация 4. х₄=(2,25+2,375)/2=2,3125. f(2,3125)= x³ - 6х + 2 » 13,3665 - 13,875 + 2 = 1,4915>0. Так как f(2,25)×f(2,375)<0, то корень находится на отрезке [2,25;2,3125], который принимаем в качестве нового доверительного. Длина его равна 0,0625 >e.

Итерация 5. х₅=(2,25+2,3125)/2»2,2825. f(2,2825)= x³ - 6х + 2 » 11,8914 - 13,6950 + 2 = 0,1964>0. Так как f(2,25)×f(2,3125)<0, то корень находится на отрезке [2,25;2,2825], который принимаем в качестве нового доверительного. Длина его равна 0,03125 >e.

Итерация 6. х₆=(2,25+2,2825)/2»2,2663. f(2,2663)= x³ - 6х + 2 » 11,6400 - 13,5978 + 2 = 0,0422>0. Так как f(2,25)×f(2,2663)<0, то корень находится на отрезке [2,25; 2,2663], который принимаем в качестве нового доверительного. Длина его равна 0,0015625 >e.

Итерация 7. х₇=(2,25+2,2663)/2»2,2582. f(2,2582)= x³ - 6х + 2 » 11,5156 - 13,5492 + 2 = - 0,0336<0. Так как f(2,25)×f(2,2663)>0, то корень находится на отрезке [2,2582; 2,2663], который принимаем в качестве нового доверительного. Длина его равна 0,00078125 < e. Следовательно, вычисления заканчиваем и последний доверительный отрезок [2,2582; 2,2663] принимаем в качестве решения задачи.

Достоинствами метода половинного деления является простота его алгоритма и гарантированная сходимость к искомому корню независимо от вида функции. Она может иметь любой непрерывный вид, в том числе – быть недифференцируемой в отдельных точках начального доверительного отрезка.

Основной недостаток - невысокая скорость сходимости по сравнению с другими методами. Также относительным недостатком является возможность случайного попадания в корень, из-за чего приходится проверять дополнительное условие ïf(x_i)ï< e_f.

Вопросы для проверки знаний.

1. Почему корректное решение задачи уточнения корня уравнения на доверительном отрезке должно учитывать погрешность вычисления функции ?

2. Каким образом в общем случае выполняются итерации при численном уточнении корня уравнения на доверительном отрезке ?

3. Что называют сходимостью метода уточнении корня уравнения на доверительном отрезке и скоростью сходимости ?

4. Какие методы уточнения корней на заданном доверительном отрезке являются наиболее употребительными ?

5. Как в методе половинного деления вычисляется очередное приближенное значение корня ?

6. Всегда ли сходится метод половинного деления и какова его скорость сходимости ?

7. Укажите достоинства и недостатки метода половинного деления уточнения корня уравнения на доверительном отрезке.

Практическое задание.

1. Уточнить по методу половинного деления корень уравнения f(x) = x⁴ - х - 14 = 0 с точностью e = 0,05 на отрезке [1,5;3].

Метод хорд

Метод половинного деления на каждой итерации i при расчете очередного приближения x_i не учитывает положение по оси Оу точек функции f(x) в краях текущего доверительного отрезка [a_i-1,b_i-1]. В методе хорд целевая функция f(x) на этом отрезке интерполируется отрезком прямой (хордой), у которого один из отрезков закреплен и приближение x_i рассчитывается как пересечение данной хорды с осью Ох. Это в общем случае позволяется ускорить сходимость метода (уменьшить число необходимых итераций) по сравнению с методом половинного деления.

Рассмотрим случай, когда закреплена точка b исходного доверительного отрезка [a; b], а точка a используется в качестве начального приближения для искомого корня: x₀ = a. Таким образом, к началу каждой итерации i доверительный интервал имеет вид: [a_i-1= х_i-1; b]. Уравнение прямой, проходящей через точки плоcкости Охy с координатами (х_i-1, f(х_i-1)) и (b, f(b)), можно представить в виде:

(x - х_i-1)/(b_i-1 - х_i-1) = (f(x) - f(х_i-1))/ (f(b) - f(х_i-1)). Подставляя в это условие значение f(x)=0, которое соответствует корню уравнения, получим выражение для абсциссы точки пересечения хорды с осью Ох: x = х_i-1 - f(х_i-1)(b - a_i-1)/ (f(b)- f(х_i-1)).

Внося в правой части полученной формулы все слагаемые под общий знаменатель и выполняя сокращения, получим схему итерационного процесса по методу хорд для закрепленной точки b:

x₀ = a; x_i = х_i-1 - f(х_i-1)(b - х_i-1)/(f(b)- f(х_i-1));(i=1,2,...). (8.8 а) При закрепленной точке b последовательность приближенных решений образует ограниченную монотонно возрастающую, ограниченную сверху точкой b (следовательно, сходящуюся) последовательность: а = x₀ < x₁< ... x_i < b.

Аналогично рассматривается случай, когда закреплена точка a исходного доверительного отрезка [a; b], а точка b используется в качестве начального приближения для искомого корня: x₀ = b. Схема итерационного имеет вид:

x₀ = b; x_i = х_i-1 - f(х_i-1)( a - х_i-1)/(f(a)- f(х_i-1));(i=1,2,...). (8.8 б)

При закрепленной точке а последовательность приближенных решений образует ограниченную монотонно убывающую, ограниченную снизу точкой а (следовательно, сходящуюся) последовательность: b = x₀ > x₁ >... > x_i > а .

В отличие от метода половинного деления, точность искомого приближенного решения оценивается не по длине содержащего его итогового доверительного отрезка, а по приращениям между очередными приближенными значениями корня. Итерационный процесс продолжается до тех пор, пока не будет выполнено условие | x_i - x_{i - 1}|< e , (8.8 в)

где e - заданная предельная величина приращений значения корня.

Метод всегда сходится, когда вторая производная целевой функции f''(x) сохраняет знак на отрезке [a; b]. Кратко правило выбора схемы итерационного процесса, обеспечивающего сходимость метода, можно сформулировать следующим образом: закреплен должен быть тот конец доверительного отрезка, для которого знак функции f (х) совпадает со знаком ее второй производной f'' (х).

При этом последовательные приближения x_n лежат по ту сторону точного корня x*, где функция f (х) имеет знак, противоположный знаку ее второй производной f'' (х).

Поскольку в методе хорд последовательность приближенных значений {x_i} монотонно стремится к искомому точному корню, здесь не возникает ситуации со случайным попаданием в корень и можно не анализировать дополнительное условие ïf(x_i)ï< e_f, как в методе половинного деления.

На рис.8.1 и 8.2 показан процесс приближения по методу хорд при f'' (x)>0 в случаях f(а) > 0 (рис.8.1) и f(b) > 0 (рис.8.2).

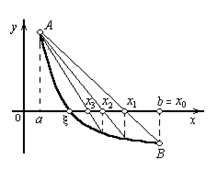
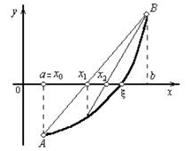
Рис.8.1. f'' (x)>0, f(а) > 0 Рис.8.2. f'' (x)>0, f(b) > 0

Пример 1. Применить метод хорд для уточнения корня уравнения f(x) = x³ - 6х + 2 = 0 из примера 1 п.8.2 с точностью e = 0,01 на отрезке [2;3].

Решение. Вторая производная целевой функции f''(x) > 0 на всем исходном отрезке [2;3]. Из примера 1 п.8.2 следует, что f(2)<0; f(3)>0. Следовательно, в качестве закрепленной принимаем точку 3, так как в ней знак функции f(х) совпадает со знаком второй производной f'' (х). Схема итерационного процесса с учетом f(3) =3³ - 6×3 + 2 = 11 принимает вид:

x₀ = 2; x_i = х_i-1 - f(х_i-1)(3- х_i-1)/(11 - f(х_i-1));(i=1,2,...).

Итерация 1. x₀ = 2; f(x₀) = f(2) =2³ - 6×2 + 2 = -2. x₁ = х₀ - f(х₀)(3- х₀)/(11 - f(х₀)) = 2 -(-2)(3- 2)/(11 -(-2)) = 2 +2/(13) = 2,1538. Приращение | x₁- x₀| = 0,1538 > e , продолжаем вычисления.

Итерация 2. x₁ = 2,1538; f(x₁) = f(2,1538) =2,1538³ - 6×2,1538 + 2 = 9,9912-12,9228 + 2 = -0,9316. x₂ = х₁ - f(х₁)(3- х₁)/(11 - f(х₁)) = 2,1538 - (-0,9316)(3- 2,1538)/(11 -(-0,9316)) = 2,2199. Приращение | x₂- x₁| = 0,0661 > e , продолжаем вычисления.

Итерация 3. x₂ = 2,2199; f(x₁) = f(2,2199) =2,2199³ - 6×2,2199+ 2 = 10,9396-13,3194 + 2 = -0,3798. x₃ = х₂ - f(х₂)(3- х₂)/(11 - f(х₂)) = 2,2199 - (-0,3798)(3- 2,2199)/(11 - (-0,3798)) = 2,2459. Приращение | x₃- x₂| = 0,0260 > e , продолжаем вычисления.

Итерация 4. x₃ = 2,2459; f(x₁) = f(2,2459) =2,2459³ - 6×2,2459+ 2 = 10,9396-13,3194 + 2 = - 0,1469. x₄ = х₃ - f(х₃)(3- х₃)/(11 - f(х₃)) = 2,2459 - (-0,1469)(3- 2,2459)/(11 - (-0,1469)) = 2,2558. Приращение | x₃- x₂| = 0,0099 < e , вычисления завершаем.

Как видно из примера, по методу хорд на поиск решения затрачено 4 итерации против 7 у метода половинного деления.

Достоинствами метода хорд является более быстрая и гарантированная сходимость к искомому корню при выполнении всех необходимых условия применения метода.

Основной недостаток - необходимость дополнительного исследования второй производной функции, что может представлять отдельную задачу.

Вопросы для проверки знаний.

1. Какое приближение применяется для целевой функции в методе хорд ?

2. Какое условие используется для завершения итерационного процесса в методе хорд ?

3. В чем заключается достаточное условие сходимости метода хорд и каково правило выбора неподвижной точки ?

4. Существует ли в методе хорд необходимость учитывать случайное попадание в корень ?

5. Какую точку следует принять в качестве закрепленной при отрицательной второй производной f'', f(а) > 0 и f(b) < 0.

Практические задания.

1. Уточнить по методу хорд корень уравнения f(x) = x⁴ - х - 14 = 0 с точностью e = 0,05 на отрезке [1,5;3].

2.Отделить положительный корень уравнения f(x) = x³ - 0,2 x² - 0,2 х - 1,2 = 0 и уточнить его с точностью e = 0,01.