Определение дифференциала и его геометрический смысл

Как уже было сказано (§1, п.1.5), если функция 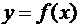в некоторой точке х = х₀ имеет конечную производную 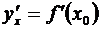, то приращение функции в этой точке может быть представлено в виде

,

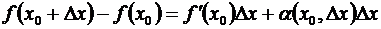где .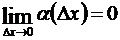

Справедливо и обратное утверждение: если приращение функции 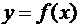в некоторой точке х = х₀ может быть представлено в виде

,

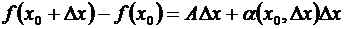то функция в этой точке имеет производную и 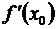= A.

Определение 1. Если приращение функции 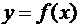в точке х может быть представлено в виде

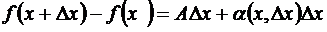, (3.12)

где 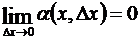, то функция называется дифференцируемой в этой точке.

Легко установить теперь справедливость следующей теоремы.

Теорема. Для того, чтобы функция 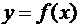была дифференцируема в некоторой точке х, необходимо и достаточно, чтобы в этой точке существовала конечная производная y' = 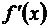. При выполнении этого условия равенство (3.12) имеет место при значении постоянной А,равном именно этой производной:

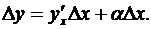(3.13)

Из этой теоремы следует, что выражения «функция дифференцируема в точке» и «функция имеет производную в точке» эквивалентны.

При 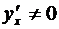наличие равенства (3.13) показывает, что произведение 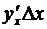есть бесконечно малая величина первого порядка малости относительно 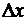, и, значит, служит для 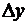ее главной частью. Произведение 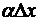всегда бесконечно малая величина высшего порядка относительно 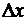, так как

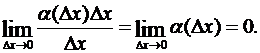
Определение 2.Главная часть 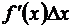приращения функции f(x) при фиксированном х называется дифференциалом функции f(x) и обозначается символом dy или df (x),

dy = 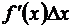. (3.14)

Чтобы истолковать геометрически дифференциал dy и его связь с приращением 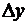функции у = f(x), рассмотрим график этой функции (рис.17).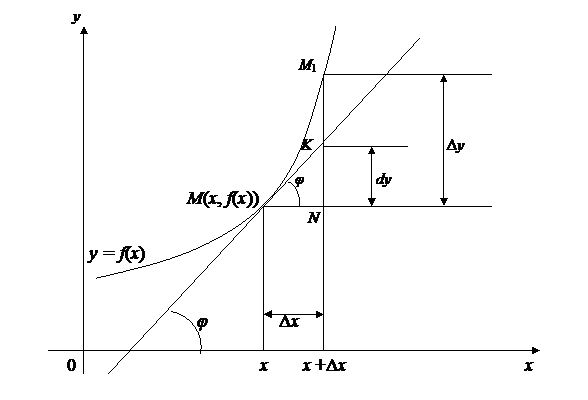

Рис. 17

Значением х аргумента и у = f(x) функции определится точка М(х, f(x)) на кривой. Проведем в этой точке кривой касательную; как мы уже видели (рис.14), ее угловой коэффициент 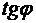равен производной 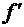(x). Если абсциссе х придать приращение 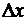, то ордината кривой f(x) получит приращение 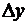= NM₁. В то же время ордината касательной получит приращение NK. Вычисляя NK как катет прямоугольного треугольника МNK, найдем: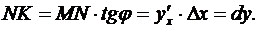

Таким образом, дифференциал функции f(x), соответствующий данным значениям х и 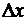, равен приращению ординаты касательной к кривой у = f(x) в данной точке х. В то же время 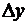есть приращение ординаты кривой.

Если отождествить дифференциал dx независимой переменной х с дифференциалом функции у = х, то дифференциал dx совпадает с приращением Dх независимой переменной х:

dx = dy = 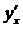·Dх = 1·Dх = Dх.(3.15)

Учитывая соглашение (3.15), можно переписать теперь формулу (3.14), дающей определение дифференциала, в виде

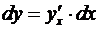(или 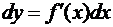) (3.16)

– так ее обычно и пишут. Отсюда получается

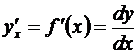. (3.17)

Таким образом, производную 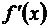, которую мы раньше представляли как цельный символ, теперь можно трактовать как дробь и рассматривать как отношение дифференциала функции к дифференциалу независимого переменного. То обстоятельство, что слева здесь стоит вполне определенное число, в то время как справа мы имеем отношение двух неопределенных чисел dy и dх (ведь dх = Dх произвольно), не должно нас смущать: числа dy и dх изменяются пропорционально, причем производная 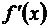как раз является коэффициентом пропорциональности.