Теорема о непрерывности функции, имеющей производную

Теорема. Если функция 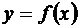в некоторой точке x = x₀ имеет (конечную) производную 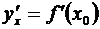, то

1) приращение функции может быть представлено в виде

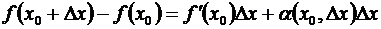, (3.6)

или, короче, 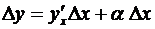, где a есть величина, зависящая от Dx и вместе с ним стремящаяся к нулю, т.е. ;

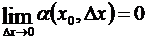2) функция в этой точке необходимо непрерывна.

Доказательство. 1) Согласно определению производной, 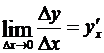. Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем

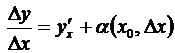, где .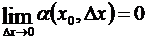

Определяя отсюда Dy, придем к формуле (3.6).

2) Чтобы доказать непрерывность функции, рассмотрим выражение (3.6). При Dx ®0 сумма в правой части (3.6) обращается в нуль. Следовательно, 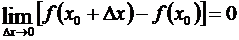, или 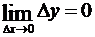, а это означает, что функция в точке x₀ непрерывна.

Из доказанной теоремы следует, что функция, имеющая производную в данной точке, будет непрерывной в этой точке. Однако непрерывная в данной точке функция не всегда имеет производную в этой точке. Так, в точке x₀ = 1 функция y = |x – 1| является непрерывной, но производной в этой точке не имеет. Это означает, что данное условие является лишь необходимым.

Производная сложной функции

Теорема. Пусть 1) функция v = j(x) имеет в некоторой точке x производную 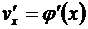, 2) функция y = f(v) имеет в соответствующей точке v производную 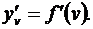Тогда сложная функция у = f(j(x)) в упомянутой точке х также будет иметь производную, равную произведению производных функций f(v) и j(x): [ f(j (x)) ]' = 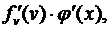или короче

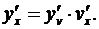(3.7)

Доказательство.Придадим х произвольное приращение Δх; пусть Δv – соответствующее приращение функции v = j(x) и, наконец, Δу – приращение функции y = f(v), вызванное приращением Δv. Воспользуемся соотношением (3.6), которое, заменяя x на v, перепишем в виде 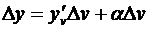(a зависит от Δv и вместе с ним стремится к нулю). Разделив его почленно на Dx, получим

.

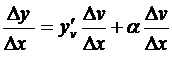Если Dx устремить к нулю, то, согласно (3.6) (при условии, что у = v), будет стремиться к нулю и Δv, а тогда, как мы знаем, будет также стремиться к нулю зависящая от Δv величина a. Следовательно, существует предел

,

который и представляет собой искомую производную .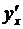

Таким образом, производная сложной функции равна произведению производной внешней функции на производную внутренней функции.

Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила (3.7). Так, если у = f(u), u = j(v), v = y (x), то

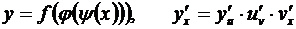. (3.8)

Примеры. 1. Пусть y = log_a sin x,иначе говоря, y = log_a v, где v = sin x. По правилу (3.7)

.

2. , т.е. y=e^u, u = v², v = sin x. По правилу (3.8)

.

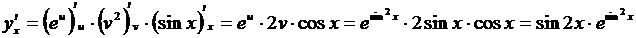1.7. Производная показательно– степенной функции

Пусть u = u(x) > 0 и v = v(x) – функции, имеющие производные в фиксированной точке x. Найдем производную функции y = u^v. Логарифмируя это равенство, получим: ln y = v ln u.

Продифференцируем обе части данного равенства по x:

.

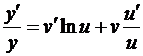Отсюда 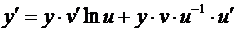, или

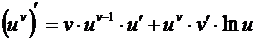. (3.9)

Таким образом, производная показательно – степенной функции состоит из двух слагаемых: первое слагаемое получается, если при дифференцировании предположить, что и есть функция от х, а v есть постоянная (т.е. рассматривать u^v как степенную функцию); второе слагаемое получается, если предположить, что v есть функция от х, а u = const (т.е. рассматривать u^v как показательную функцию).

Примеры.1. Если y = x^{tg x}, то, полагая u = x, v = tg x,согласно (3.9) имеем

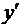= tg x x^{tg x – 1} + x^{tg x} ln x sec²x.

Прием, примененный в данном случае для нахождения производной и состоящий в том, что сначала находят производную логарифма рассматриваемой функции, широко применяется при дифференцировании функций: при отыскании производной функции эти функции сначала логарифмируют, а затем из равенства, полученного после дифференцирования логарифма функции, определяют производную функции. Такая операция называется логарифмическим дифференцированием.

2.Требуется найти производную от функции

.

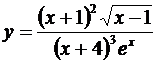Логарифмируя, находим:

ln y = 2ln(x + 1) + 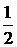ln(x – 1) – 3 ln(x + 4) – x.

Дифференцируем обе части последнего равенства:

.

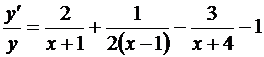Умножая на у и подставляя вместо у, получаем:

.
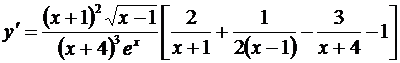