ВОПРОС№20: Теорема существования и непрерывности обратной функции.
Теорема (о существовании и непрерывности обратной функции). Пусть на интервале (a,b) определена непрерывная возрастающая (убывающая)функция y=f(x). Обозначим
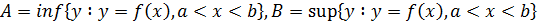
Тогда на интервале (А, В) определена обратная функция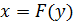 
, которая возрастает(убывает) на этом интервале и является непрерывной в каждой точке этого интервала.
ВОПРОС№22: Дифференцируемые функции. Критерий дифференцируемости
Определение. Функция f, определенная в окрестности точки x , называется дифференцируемой в этой точке, если верна формула
f ( x штрих + ▲x штрих ) - f ( x штрих ) =S Ai ▲xi +Sai ( ▲x штрих )▲xi (3)
где i A – числа, а функции ai (▲ x штрих ) удовлетворяют условию
ai(▲ x штрих )→ 0 (i =1,2,…, n)при ▲ x →0 . (4)
Теорема. Пусть функция f дифференцируема в точке x .Тогда в этой точке у нее существуют частные производные и выполнены равенства
(df( x штрих))/ (dxi)= Ai(i=1,2,…,n).
Доказательство. Из формулы (3) следует, что
(f ( x1 ,...,xi-1 ,xi+▲ xi ,xi+1,...,xn )- f ( x1 ,...,xi-1 ,xi ,xi+1 ,...,x n))/(▲Xi)= Ai+αi(▲Xi).
Переходя к пределу при ▲xi → 0, получим равенство (5).
Теорема(достаточные условия дифференцируемости функции). Если функция f имеет частные производные по всем переменным в некоторой окрестности точки x штрих ,причем все эти частные производные непрерывны в самой
точке x штрих ,то указанная функция дифференцируема в этой точке.
Теорема (критерий дифференцируемости функции). Функция f (x), определенная в окрестности точки x , дифференцируема в этой точке тогда и только тогда, когда существует производная f ׳(x). При этом F = f ׳(x).
Доказательство. Пусть существует производная f ׳(x ). Обозначим
a( t) =(((f(t)-f(x)) /(t-x )) -f׳ (x)
Тогда
f(t ) =f (x )+ ( t-x ) f׳( x)+ ( t-x)α (t ),( α( t)→0). (2)
Пусть теперь выполнено равенство (1) . Тогда
(( f(t)-f(x)) /(t-x ) = F+ α(t ) ,limα(t) = 0.
Следовательно, существует производная f ׳(x)= F .
ВОПРОС№23: Производная суммы, разности, произведения и частного двух функций.
Производная суммы и разности
Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:
1. (f + g)’ = f ’ + g ’
2. (f − g)’ = f ’ − g ’
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.
Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.
· Задача. Найти производные функций: f(x) = x2 + sin x; g(x) = x4 + 2x2 − 3.
Решение. Функция f(x) — это сумма двух элементарных функций, поэтому:
f ’(x) = (x2 + sin x)’ = (x2)’ + (sin x)’ = 2x + cos x;
Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):
g ’(x) = (x4 + 2x2 − 3)’ = (x4 + 2x2 + (−3))’ = (x4)’ + (2x2)’ + (−3)’ = 4x3 + 4x + 0 = 4x · (x2 + 1).
Ответ:
f ’(x) = 2x + cos x;
g ’(x) = 4x · (x2 + 1).
Производная произведения
Производная произведения считается совсем по другой формуле. А именно:
(f · g) ’ = f ’ · g + f · g ’
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
· Задача. Найти производные функций: f(x) = x3 · cos x; g(x) = (x2 + 7x − 7) · ex.
Решение. Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x3 · cos x)’ = (x3)’ · cos x + x3 · (cos x)’ = 3x2 · cos x + x3 · (− sin x) = x2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x2 + 7x − 7) · ex)’ = (x2 + 7x − 7)’ · ex + (x2 + 7x − 7) · (ex)’ = (2x + 7) · ex + (x2 + 7x − 7) · ex = ex · (2x + 7 + x2 + 7x −7) = (x2 + 9x) · ex = x(x + 9) · ex.
Ответ:
f ’(x) = x2 · (3cos x − x · sin x);
g ’(x) = x(x + 9) · ex.
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.
Производная частного
Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:
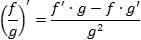
Неслабо, да? Откуда взялся минус? Почему g2? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.
Задача. Найти производные функций: f(x) = x3 · cos x; g(x) = (x2 + 7x − 7) · ex.
Решение. Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x3 · cos x)’ = (x3)’ · cos x + x3 · (cos x)’ = 3x2 · cos x + x3 · (− sin x) = x2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x2 + 7x − 7) · ex)’ = (x2 + 7x − 7)’ · ex + (x2 + 7x − 7) · (ex)’ = (2x + 7) · ex + (x2 + 7x − 7) · ex = ex · (2x + 7 + x2 + 7x −7) = (x2 + 9x) · ex = x(x + 9) · ex.
Ответ:
f ’(x) = x2 · (3cos x − x · sin x);
g ’(x) = x(x + 9) · ex