I. Дифференцирование явных функций
Правила дифференцирования:
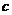 – постоянная,
– постоянная, 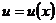 ,
, 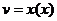 – дифференцируемые функции:
– дифференцируемые функции:
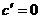 (7.2)
(7.2) 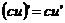 (7.6)
(7.6)
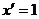 (7.3)
(7.3) 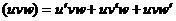 (7.7)
(7.7)
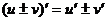 (7.4)
(7.4) 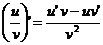 ,
, 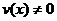 (7.8)
(7.8)
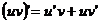 (7.5)
(7.5) 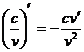 ,
, 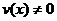 (7.9)
(7.9)
Производная сложной функции. Если 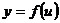 ,
, 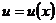 , т.е.
, т.е. 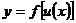 , где
, где 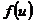 и
и 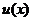 имеют производные, то
имеют производные, то
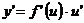 (7.10)
(7.10)
Производная обратной функции. Если 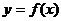 – дифференцируемая и строго монотонная функция на промежутке
– дифференцируемая и строго монотонная функция на промежутке 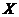 , то функция обратная к данной
, то функция обратная к данной 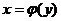 , также дифференцируема и ее производная определяется соотношением:
, также дифференцируема и ее производная определяется соотношением:
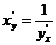 ,
, 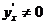 . (7.11)
. (7.11)
Логарифмическая производная. Логарифмической производной функции 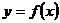 называется производная от логарифма этой функции, т.е.
называется производная от логарифма этой функции, т.е.
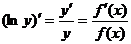 . (7.12)
. (7.12)
Формулы дифференцирования основных элементарных функций:
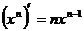 (7.13)
(7.13) 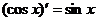 (7.20)
(7.20)
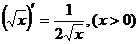 (7.14)
(7.14) 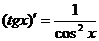 (7.21)
(7.21)
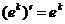 (7.15)
(7.15) 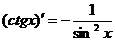 (7.22)
(7.22)
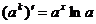 (7.16)
(7.16) 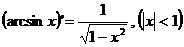 (7.23)
(7.23)
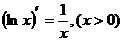 (7.17)
(7.17) 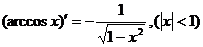 (7.24)
(7.24)
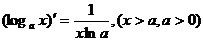 (7.18)
(7.18) 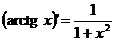 (7.25)
(7.25)
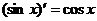 (7.19)
(7.19) 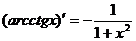 (7.26)
(7.26)
II. Дифференцирование неявных функций
Если зависимость между  и
и 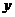 задана в неявной форме уравнением
задана в неявной форме уравнением 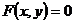 , то для нахождения производной функции
, то для нахождения производной функции 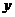 необходимо продифференцировать по
необходимо продифференцировать по  обе части данного уравнения, рассматривая
обе части данного уравнения, рассматривая 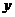 как функцию от
как функцию от  .Из полученного уравнения первой степени (относительно
.Из полученного уравнения первой степени (относительно 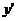 ) находится
) находится 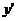 .
.
III. Дифференцирование функций, заданных параметрически.
Если функция аргумента  заданнапараметрически уравнениями
заданнапараметрически уравнениями 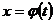 и
и 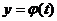 , то
, то
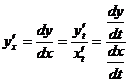 . (7.27)
. (7.27)
IV. Производные высших порядков.
Производные п-го порядка называется производная от производной 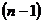 -го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции:
-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции:
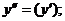
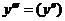 ; …;
; …; 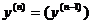 . (7.28)
. (7.28)
Если функция задана параметрически, то
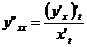 ;
; 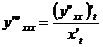 ; …;
; …; 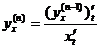 . (7.29)
. (7.29)
3. Найти производные функций:
а) 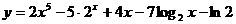 ; б)
; б) 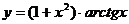 ;
;
в) 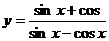 ; г)
; г) 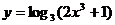 .
.
Решение.
а) Используя правила дифференцирования (7.2), (7.4), (7.6) и формулы (7.13), (7.16) и (7.17) получим
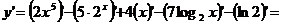
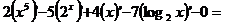
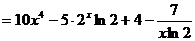 .
.
б) Используя правила дифференцирования (7.5) и формулу (7.25), получим:
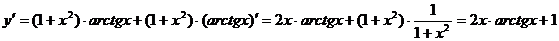
.
в) Используя правила дифференцирования (7.8) и формулы (7.19) и (7.20), получим:
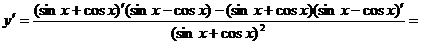
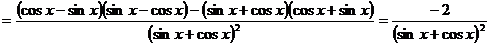 .
.
г) Используя правила дифференцирования сложной функции (7.10) и формулы (7.13) и (7.18), получим:
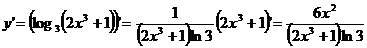 .
.
4. Найти производную 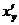 обратной функции, если
обратной функции, если 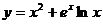 .
.
Решение. Находим производную функцию 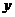 по переменной
по переменной  :
:
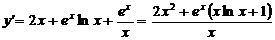 .
.
Следовательно, согласно соотношению (7.11), получи:
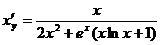 .
.
5.Найти производные функций:
а) 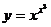 ; б)
; б) 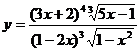 .
.
Решение.
а) Имеем показательно-степенную функцию. Используя метод логарифмического дифференцирования (7.12) получим:
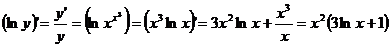 .
.
Отсюда имеем:
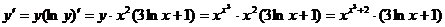 .
.
б) Здесь заданную функцию также целесообразно прологарифмировать:
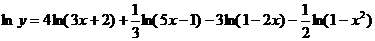 .
.
Найдем производную:
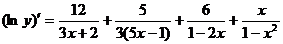 .
.
Тогда, согласно формуле (7.12), получим
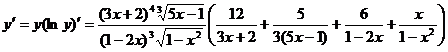 .
.
6.Найти производную 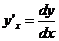 неявной функции
неявной функции 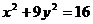 .
.
Решение. Так как 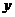 является функцией от
является функцией от  , то будем рассматривать
, то будем рассматривать 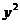 как сложную функцию от
как сложную функцию от  . Продифференцировав обе части данного уравнения по
. Продифференцировав обе части данного уравнения по  , имеем
, имеем
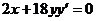 .
.
Разрешая последнее уравнение относительно 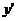 , получим:
, получим:
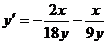 .
.
7.17. Найти производную 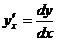 функции, заданной параметрически:
функции, заданной параметрически:
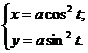
Решение. Используя правила дифференцирования функции, заданной параметрически (7.27), найдем:
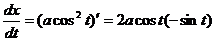 и
и 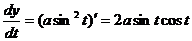 .
.
Отсюда 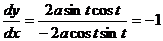 .
.
7.18. Найти производную 4-го порядка от функции 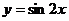 .
.
Решение. Последовательно дифференцируя функцию, получим:
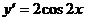 ;
; 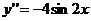 ;
; 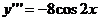 ;
; 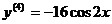 .
.
7.19. Найти производную второго порядка от функции, заданной параметрически:
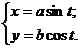
Решение. Последовательно дифференцируя функцию, получим:
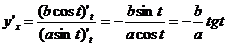 ;
;
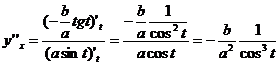 .
.
7.20. Найти производную n-го порядка от функции 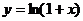 .
.
Решение. Последовательно дифференцируя функцию, получим:
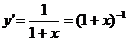 ;
; 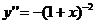 ;
; 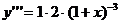 ;
;
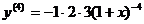 ; … ;
; … ;
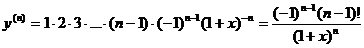 .
.
Найти производные функций:
7.21. 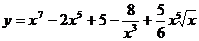 .
.
7.27. 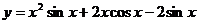
7.29. 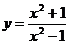 .
.
7.35. 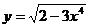
7.45. 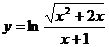 .
.
7.49. 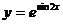 .
.
7.57. 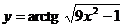 .
.
7.65. 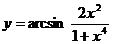 .
.
Найти производные 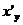 обратных функций:
обратных функций:
7.71. 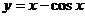 7.72.
7.72. 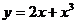 7.75.
7.75. 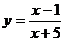 .
.
Найти производные 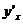 от неявных функций:
от неявных функций:
7.76 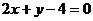
7.77. 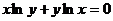
7.79 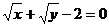 .
.
7.82. 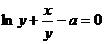
7.84. 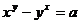
7.85 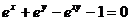 .
.
Найти производные функций, заданных параметрически:
7.89. 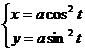 7.90.
7.90. 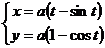 7.91.
7.91. 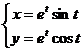 .
.
Найти производные второго порядка функций:
7.94 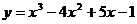 7.95.
7.95. 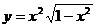 7.97.
7.97. 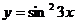 .
.
Найти производные 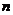 -го порядка функций:
-го порядка функций:
7.100. 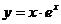 7.101.
7.101. 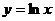 7.104.
7.104. 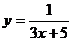 .
.
7.106.Показать, что функция 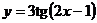 удовлетворяет уравнению
удовлетворяет уравнению 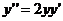 .
.
7.107.Показать, что функция 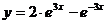 удовлетворяет уравнению
удовлетворяет уравнению 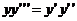 .
.
7.108.Показать, что функция 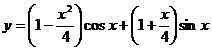 удовлетворяет уравнению
удовлетворяет уравнению 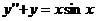 .
.
7.3. Геометрические и механические приложения производной
Краткая теория
1. Геометрический смысл производной. Если кривая задана уравнением 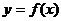 или
или 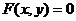 , то
, то 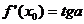 есть угловой коэффициент касательной (тангенс угла ее наклона с положительным направлением оси абсцисс).
есть угловой коэффициент касательной (тангенс угла ее наклона с положительным направлением оси абсцисс).
Уравнение касательной к кривой 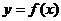 в точке
в точке 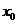 имеет вид:
имеет вид:
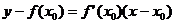 , (7.30)
, (7.30)
а уравнение нормали:
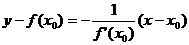 . (7.31)
. (7.31)
Углом между двумя кривыми 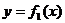 ,
, 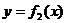 в точке их пересечения
в точке их пересечения 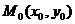 называется угол между касательными к этим кривым в точке
называется угол между касательными к этим кривым в точке 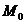 , тангенс которого находится по формуле:
, тангенс которого находится по формуле:
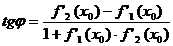 . (7.32)
. (7.32)
2. Механический смысл производной. Если точка движения по закону 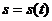 , где
, где 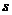 - путь,
- путь, 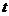 - время, то
- время, то 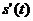 представляет скорость изменения пути в момент
представляет скорость изменения пути в момент 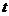 . Вторая производная пути по времени
. Вторая производная пути по времени 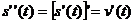 есть скорость изменения скорости или ускорение точки в момент
есть скорость изменения скорости или ускорение точки в момент 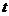 .
.
7.109. Составить уравнение касательной и нормали к графику функции 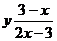 в точке с абсциссой
в точке с абсциссой 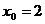 .
.
Решение. Вычислим значение функции в точке 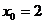 :
: 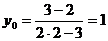 . Производная функции
. Производная функции 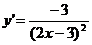 . Значение производной в точке
. Значение производной в точке 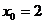 :
: 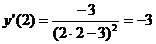 . Согласно (7.30), уравнение касательной имеет вид:
. Согласно (7.30), уравнение касательной имеет вид: 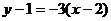 , или
, или 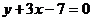 , а уравнение нормали (7.31) -
, а уравнение нормали (7.31) - 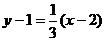 , или
, или 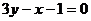 .
.
7.110. Составить уравнение касательной к графику функции 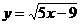 , проходящей через точку
, проходящей через точку 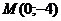 .
.
Решение. Определим абсциссу точки касания из условия, что точка 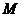 принадлежит касательной, т.е. ее координаты удовлетворяют уравнению (7.30):
принадлежит касательной, т.е. ее координаты удовлетворяют уравнению (7.30): 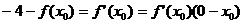 .
.
Подставляя в это соотношение выражение для значения функции и ее производной в точке 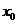 , получим уравнение вида:
, получим уравнение вида: 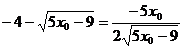 . Решая его относительно
. Решая его относительно 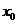 , найдем, что
, найдем, что 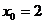 . Определив значение функции и ее производной в этой точке, уравнение касательной запишем в виде:
. Определив значение функции и ее производной в этой точке, уравнение касательной запишем в виде: 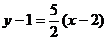 , или
, или 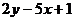 .
.
7.111. Составить уравнение касательной и нормали в точке (1; 4) к кривой, заданной параметрически: 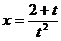 ,
, 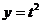 .
.
Решение. Найдем значение 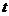 , при котором
, при котором 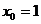 ,
, 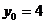 , из решения системы:
, из решения системы: 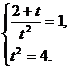 Получим, что
Получим, что 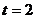 .
.
Производную определим по формуле (7.27): 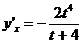 .
.
Значение производной при 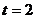 :
: 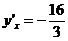 .
.
Тогда уравнение касательной запишется в виде: 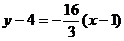 , или
, или 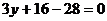 , а уравнение нормали примет вид:
, а уравнение нормали примет вид: 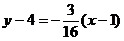 , или
, или 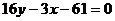 .
.
7.112. Найти угол между параболами 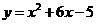 и
и 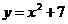 в точке их пересечения.
в точке их пересечения.
Решение. Решив совместно систему уравнений парабол, находим точку их пересечения: 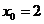 и
и 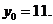 Продифференцировав уравнения парабол
Продифференцировав уравнения парабол 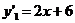 ,
, 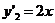 , найдем их угловые коэффициенты в точке пересечения:
, найдем их угловые коэффициенты в точке пересечения: 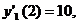
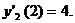 Согласно (7.32), тангенс угла между параболами будет равен:
Согласно (7.32), тангенс угла между параболами будет равен: 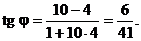 Следовательно,
Следовательно, 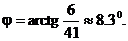
Составить уравнение касательной и нормали к кривым в указанных точках:
7.113. 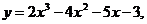
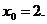
7.114. 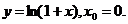
7.115. 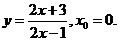
7.116. 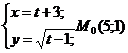
7.117. 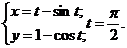
7.118. 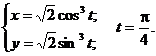
7.119. 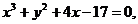
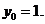
7.120. 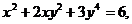
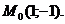
7.121. Какой угол образует с осью абсцисс касательная к графику функции, проведенная в указанной точке? Написать уравнение касательной:
а) 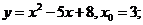 б)
б) 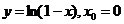
7.122. Составить уравнение касательной к кривой 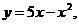 параллельной прямой, проходящей через точки (1;7) и (-2;2).
параллельной прямой, проходящей через точки (1;7) и (-2;2).
7.123. Составить уравнения касательных к кривой 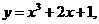 перпендикулярных прямой
перпендикулярных прямой 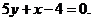
7.124. Составить уравнение касательной к кривой 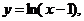 перпендикулярной прямой, образующей с осью абсцисс угол
перпендикулярной прямой, образующей с осью абсцисс угол 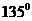 .
.
7.125.Составить уравнения касательных к кривой 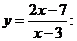
а) параллельных прямой 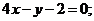
б) перпендикулярных прямой 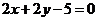 .
.
7.126. Составить уравнение касательной к кривой 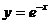 :
:
а) проходящей параллельно биссектрисе второго и четвертого координатных углов;
б) отсекающей на оси абсцисс отрезок, равный –1.
7.127. Составить уравнение касательной к графику функции 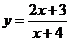 , проходящей через точку М (6; 2).
, проходящей через точку М (6; 2).
7.128. Найти угол между кривыми:
а) 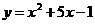 и
и 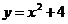 ; б)
; б) 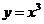 и
и 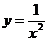 ; в)
; в) 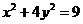 и
и 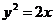 .
.
7.129. Тело движется прямолинейно по закону s(t). Определить скорость и ускорение тела в указанный момент времени 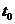 :
:
а) 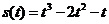 ,
, 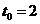 ; б)
; б) 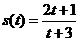 ,
, 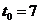 .
.
7.130.Тело, брошенное вертикально вверх, движется по закону: 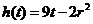 . Найти начальную скорость и ускорение тела (
. Найти начальную скорость и ускорение тела ( 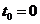 ) и максимальную высоту подъема (при которой скорость
) и максимальную высоту подъема (при которой скорость 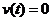 ).
).
7.4. Предельный анализ экономических процессов
Краткая теория
1. Предельные величины. Применение производной в экономике позволяет получать так называемые предельные характеристики экономических объектов или процессов. Предельные величины (предельная выручка, полезность, производительность, предельный доход, продукт и др.) характеризуют не состояние, а скорость изменения экономического объекта или процесса по времени или относительно другого исследуемого фактора.
Издержки производства.Если издержки производства 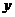 рассматривать как функцию выпускаемой продукции
рассматривать как функцию выпускаемой продукции  , т.е.
, т.е. 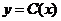 , то
, то 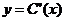 будет выражать предельные издержки производства и приближенно характеризовать прирост переменных затрат на производство дополнительной единицы продукции. Средние издержки являются издержками на единицу выпуска продукции:
будет выражать предельные издержки производства и приближенно характеризовать прирост переменных затрат на производство дополнительной единицы продукции. Средние издержки являются издержками на единицу выпуска продукции: 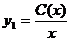 .
.
2. Производительность труда. Пусть функция 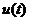 выражает объем произведенной продукции
выражает объем произведенной продукции 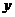 за время
за время 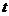 . Тогда производная объема произведенной продукции по времени
. Тогда производная объема произведенной продукции по времени 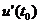 есть производительность труда в момент
есть производительность труда в момент 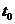 .
.
3. Функция потребления и сбережения. Если  - национальный доход,
- национальный доход, 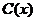 - функция потребления (часть дохода, которая тратится), а
- функция потребления (часть дохода, которая тратится), а 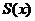 - функция сбережения, то
- функция сбережения, то
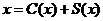 . (7.33)
. (7.33)
Дифференцируя, получим, что
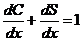 , (7.34)
, (7.34)
где 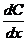 - предельная склонность к потреблению;
- предельная склонность к потреблению; 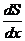 - предельная склонность к сбережению.
- предельная склонность к сбережению.
4. Эластичность. Эта мера реагирования одной переменной величины на изменение другой. Эластичность функции приближенно показывает, на сколько процентов изменится одна переменная в результате изменения другой переменной на 1%.
Эластичность функции определяется с помощью соотношения:
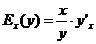 или
или 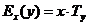 , (7.35)
, (7.35)
где
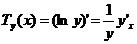 (7.36)
(7.36)
– относительная скорость изменения (темп) функции.
Эластичность функции применяется при анализе спроса и предложения от цены (ценовая эластичность). Она показывает реакцию спроса или предложения на изменение цены и определяет, на сколько процентов приближенно изменится спрос или предложение при изменении цены на 1%.
Если эластичность спроса 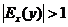 , то спрос считается эластичным, если
, то спрос считается эластичным, если 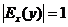 – нейтральным (с единичной эластичностью), а если
– нейтральным (с единичной эластичностью), а если 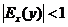 – неэластичным относительно цены.
– неэластичным относительно цены.
7.131. Функция издержек производства продукции некоторой фирмой имеет вид: 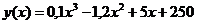 (ден. ед.). Найти средние и предельные издержки производства и вычислить их значение при
(ден. ед.). Найти средние и предельные издержки производства и вычислить их значение при 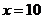 .
.
Решение. Найдем производную 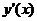 и ее значение
и ее значение 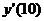 - предельные издержки производства:
- предельные издержки производства:
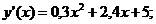
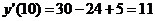 .
.
Средние издержки:
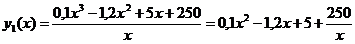 ;
;
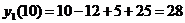 .
.
Это означает, что при данном уровне производства (количестве выпускаемой продукции) средние затраты на производство одной единицы продукции составляют 28 ден. ед., а увеличение объема на одну единицу продукции обойдется фирме приближенно в 11 ден. ед.
7.132. Функция потребления некоторой страны имеет вид:
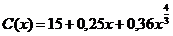 ,
,
где  - совокупный национальный доход (ден. ед.). Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27 ден. ед.
- совокупный национальный доход (ден. ед.). Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27 ден. ед.
Решение:Предельная склонность к потреблению: 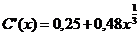 ; ее значение:
; ее значение: 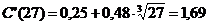 .
.
Предельная склонность к сбережению:
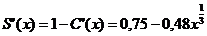 ; ее значение:
; ее значение: 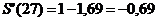 .
.
7.133. Объем производства зимней обуви 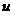 , выпускаемый некоторой фирмой, может описан уравнением
, выпускаемый некоторой фирмой, может описан уравнением 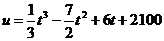 (ед), где
(ед), где 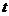 - календарный месяц года. Вычислить производительность труда, скорость и темп ее изменения: а) в начале года (
- календарный месяц года. Вычислить производительность труда, скорость и темп ее изменения: а) в начале года ( 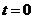 ); б) в середине года (
); б) в середине года ( 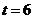 ); в) в конце года (
); в) в конце года ( 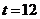 ).
).
Решение. Производительность труда выражается производной 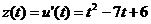 (ед./мес.), а скорость и темп изменения производительности – соответственно производной
(ед./мес.), а скорость и темп изменения производительности – соответственно производной 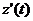 и логарифмической производной
и логарифмической производной  :
: 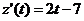 (ед./мес.2),
(ед./мес.2), 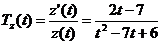 (ед./мес.).
(ед./мес.).
В заданные моменты времени соответственно имеем 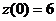 (ед./мес.),
(ед./мес.), 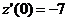 (ед./мес2.),
(ед./мес2.), 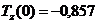 (ед./мес.),
(ед./мес.), 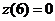 (ед./мес.),
(ед./мес.), 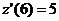 (ед./мес2.),
(ед./мес2.), 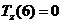 (ед./мес.),
(ед./мес.), 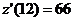 (ед./мес.2),
(ед./мес.2), 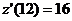 (ед./мес.2),
(ед./мес.2), 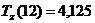 (ед./мес.).
(ед./мес.).
7.134. Функция спроса 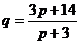 и предложение
и предложение 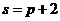 , где
, где 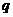 и
и 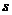 - количество товаров, соответственно покупаемого и предлагаемого на продажу в единицу времени,
- количество товаров, соответственно покупаемого и предлагаемого на продажу в единицу времени, 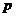 - цена единицы товара. Найти: а) равновесную цену, то есть цену, при которой спрос и предложение уравновешиваются; б) эластичность спроса и предложения; в) изменение дохода при увеличении цены на 10% от равновесной.
- цена единицы товара. Найти: а) равновесную цену, то есть цену, при которой спрос и предложение уравновешиваются; б) эластичность спроса и предложения; в) изменение дохода при увеличении цены на 10% от равновесной.
Решение: а) Равновесная цена определяется из условия 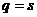 , т.е.
, т.е. 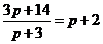 ; откуда
; откуда 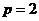 , т.е. равновесная цена равна 2 ден. ед.
, т.е. равновесная цена равна 2 ден. ед.
б) Найдем эластичности по спросу и предложению по формуле (7.35):
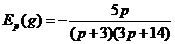 ;
; 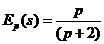 .
.
Для равновесной цены 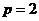 имеем
имеем 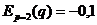 ;
; 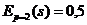 .
.
Так как полученные значения эластичности меньше 1 (по абсолютной величине), то спрос и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это означает, что изменение цены не приведет к резкому изменению спроса и предложения.
в) При увеличении цены 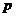 на 10% от равновесной спрос уменьшается на
на 10% от равновесной спрос уменьшается на 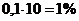 , следовательно, доход
, следовательно, доход 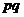 возрастает приближенно на 9%.
возрастает приближенно на 9%.
7.135. Зависимость между спросом 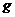 и ценой
и ценой 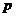 за единицу продукции, выпускаемой некоторым предприятием, дается соотношением
за единицу продукции, выпускаемой некоторым предприятием, дается соотношением 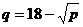 . Найти эластичность спроса. Выяснить, при каких значениях цены спрос является эластичным, нейтральным и неэластичным. Какие рекомендации о цене за единицу продукции можно дать руководителям предприятия при
. Найти эластичность спроса. Выяснить, при каких значениях цены спрос является эластичным, нейтральным и неэластичным. Какие рекомендации о цене за единицу продукции можно дать руководителям предприятия при 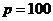 и при
и при 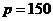 ден. ед.?
ден. ед.?
Решение. Эластичность спроса по формуле (7.35) есть 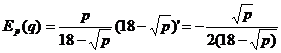 .
.
Спрос нейтрален, если 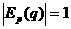 . Решая это уравнение, имеем
. Решая это уравнение, имеем 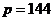 . Далее, принимая во внимание, что
. Далее, принимая во внимание, что 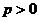 и
и 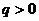 (т.е.
(т.е. 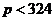 ), получим, что если
), получим, что если 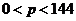 - спрос является неэластичным; при
- спрос является неэластичным; при 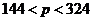 - спрос эластичен.
- спрос эластичен.
Рекомендации. Если цена единицы продукции составляет 100 ден. ед., то спрос является неэластичным и можно повысить цену продукции, выручка при этом будет расти. При стоимости продукции 150 ден. ед. спрос является эластичным. В данном случае целесообразно рассмотреть предложение о снижении цены, выручка от реализации будет расти в результате увеличения спроса на продукцию.
7.136. Задана функция 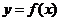 полных затрат предприятия на производство
полных затрат предприятия на производство  единиц продукции. Определить связь между коэффициентом эластичности полных и средних затрат.
единиц продукции. Определить связь между коэффициентом эластичности полных и средних затрат.
Решение. Средние затраты на единицу продукции равны: 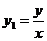 . По формуле (7.35.) коэффициенты эластичности полных и средних затрат равны:
. По формуле (7.35.) коэффициенты эластичности полных и средних затрат равны: 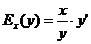 ;
;
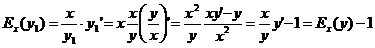 , т.е. коэффициент эластичности средних затрат на единицу меньше коэффициента эластичности полных затрат.
, т.е. коэффициент эластичности средних затрат на единицу меньше коэффициента эластичности полных затрат.
7.137. Зависимость между издержками производства и объемом выпускаемой продукции  на предприятии выражается функцией
на предприятии выражается функцией  . Определить средние и предельные издержки при объеме продукции 10 ед.
. Определить средние и предельные издержки при объеме продукции 10 ед.
7.138. Выручка от продажи конфет составляет 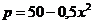 , где
, где  - объем проданной продукции (тыс. ед.). Найти среднюю и предельную выручку, если продано: а) 10 тыс. ед.; б) 60 тыс. ед.
- объем проданной продукции (тыс. ед.). Найти среднюю и предельную выручку, если продано: а) 10 тыс. ед.; б) 60 тыс. ед.
7.139. Функция издержек производства 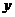 от объема выпускаемой продукции
от объема выпускаемой продукции  имеет вид
имеет вид 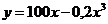 . Определить средние и предельные издержки при объеме продукции 10 ед.
. Определить средние и предельные издержки при объеме продукции 10 ед.
7.140. Себестоимость продукции 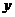 связана с объемом выпускаемой продукции
связана с объемом выпускаемой продукции  уравнением:
уравнением: 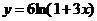 . Определить среднюю и предельную себестоимость выпускаемой продукции при объеме, равной 10 ед.
. Определить среднюю и предельную себестоимость выпускаемой продукции при объеме, равной 10 ед.
7.141. Производительность труда бригады может описана уравнением 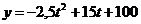 , где
, где 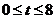 - рабочее время в часах. Вычислить скорость и темп изменения производительности труда при
- рабочее время в часах. Вычислить скорость и темп изменения производительности труда при 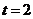 и
и 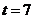 .
.
7.142. Себестоимость производства телевизоров 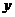 (в тыс. руб.) описывается функцией
(в тыс. руб.) описывается функцией 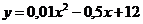 ,
, 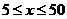 , где
, где  - объем выпускаемой продукции в месяц (тыс. ед.). Определить скорость и темп изменения себестоимости и при выпуске 20 и 40 тыс. ед. продукции.
- объем выпускаемой продукции в месяц (тыс. ед.). Определить скорость и темп изменения себестоимости и при выпуске 20 и 40 тыс. ед. продукции.
7.143. Функция потребления некоторой страны имеет вид: 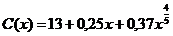 , где
, где  - совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 32.
- совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 32.
7.144. Функция потребления некоторой страны имеет вид: 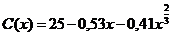 , где
, где  - совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27.
- совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27.
7.145. Зависимость между себестоимостью готовой продукции предприятия 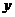 (млн. руб.) и объемом выпускаемых изделий
(млн. руб.) и объемом выпускаемых изделий  (тыс. шт.) выражается уравнением
(тыс. шт.) выражается уравнением 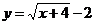 . Найти эластичность себестоимости продукции предприятия, выпускающего 12 тыс. шт. изделий. Какие рекомендации можно дать руководителям предприятия об изменении величины объема выпускаемой продукции?
. Найти эластичность себестоимости продукции предприятия, выпускающего 12 тыс. шт. изделий. Какие рекомендации можно дать руководителям предприятия об изменении величины объема выпускаемой продукции?
7.146. Функция полных затрат в зависимости от объема выпускаемой продукции задана соотношением: 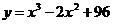 . При каком объеме производства предельные и средние затраты совпадают? Найти коэффициенты эластичности полных и средних затрат при данном объеме.
. При каком объеме производства предельные и средние затраты совпадают? Найти коэффициенты эластичности полных и средних затрат при данном объеме.
7.147. Зависимость между объемом выпуска готовой продукции 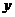 (млн. руб.) и объемом производственных фондов
(млн. руб.) и объемом производственных фондов  (млн. руб.) выражается уравнением
(млн. руб.) выражается уравнением 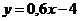 . Найти эластичность выпуска продукции для предприятия, имеющего фонды в размере 40 млн. руб.
. Найти эластичность выпуска продукции для предприятия, имеющего фонды в размере 40 млн. руб.
7.148. Зависимость между себестоимостью единицы продукции 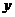 (в руб.) и выпуском продукции
(в руб.) и выпуском продукции  (в млн. руб.) выражается уравнением
(в млн. руб.) выражается уравнением 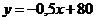 . Найти эластичность себестоимости при выпуске продукции на 30 млн. руб.
. Найти эластичность себестоимости при выпуске продукции на 30 млн. руб.
7.149. Зависимость между количеством выпускаемых деталей в партии  (тыс. ед.) и затратами на их изготовление
(тыс. ед.) и затратами на их изготовление 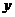 (тыс. руб.) для предприятия отрасли выражается уравнением
(тыс. руб.) для предприятия отрасли выражается уравнением 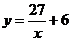 . Найти эластичность затрат для предприятий, выпускающих по 10 тыс. деталей в партии.
. Найти эластичность затрат для предприятий, выпускающих по 10 тыс. деталей в партии.
7.150. Найти эластичность функции спроса при заданной стоимости 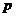 :
:
а) 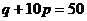 ,
, 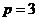 ; б)
; б) 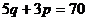 ,
, 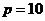 ; в)
; в) 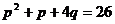 ,
, 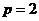 и
и 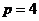 .
.
7.151. Для следующих функций спроса найти значение 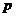 , при которых спрос является эластичным: а)
, при которых спрос является эластичным: а) 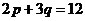 ; б)
; б) 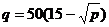 ; в)
; в)  .
.
7.152. Задана функция спроса 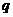 и предложения
и предложения 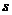 от цены
от цены  :
: 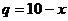 ,
, 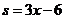 . Найти: а) равновесную цену; б) эластичность спроса и предложен
. Найти: а) равновесную цену; б) эластичность спроса и предложен
