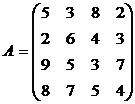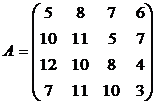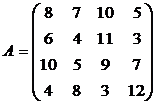Решение игры в общем виде. Сведение задачи по теории игр к паре взаимодвойственных задач линейного программирования

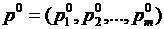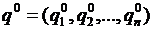Если игра т х п не имеет оптимального решения непосредственно в чистых стратегиях, то оптимальное решение необходимо искать в области смешанных стратегий. Игрок А обладает стратегиями А₁, А₂,…, А_m, а игрок В – стратегиями B₁, B₂,…, B_n. Необходимо определить оптимальные стратегии и , где 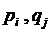- вероятности применения соответствующих чистых стратегий А_i, B_j. При этом 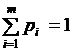и .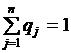

Если игрок А применяет смешанную стратегию 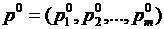против любой чистой стратегии В_j игрока В, то он получает средний выигрыш (математическое ожидание выигрыша):

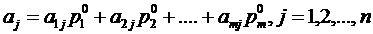
Для оптимальной стратегии 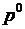все средние выигрыши не меньше выигрыша игры v, поэтому получаем систему неравенств:

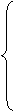a₁₁p₁+ a₂₁p₂+…+ a_m1p_m ≥ v

a₁₂p₁+ a₂₂p₂+…+ a_m2p_m ≥ v

………………………………

a_1np₁+ a_2np₂+…+ a_mnp_m ≥ v

Если каждое неравенство разделить на число v>0 (v>0 можно добиться, сделав все элементы a_ij ≥ 0) и введя новые переменные:

x₁=p₁/v, x₂=p₂/v, …., x_m=p_m/v

предыдущая система примет вид:

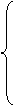a₁₁x₁+ a₂₁x₂+…+ a_m1x_m ≥ 1

a₁₂x₁+ a₂₂x₂+…+ a_m2x_m ≥ 1

………………………………

a_1nx₁+ a_2nx₂+…+ a_mnx_m ≥ 1

Если нормировочное условие, выраженное равенством p₁+ p₂+…+ p_m =1 разделить также на v, тополучим, что переменные x₁+x₂+…+x_m=1/v. В силу того, что цель игрока А максимизировать свой выигрыш, т.е. максимизировать цену игры v, максимизация цены игры v эквивалентна минимизации величины 1/v. Поэтому задача в терминах линейного программирования может быть сформулирована следующим образом:

Найти минимум целевой функции Z = x₁+x₂+…+ x_m при ограничениях. Тем самым получаем задачу линейного программирования, решая которую получим оптимальную стратегию 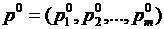и цену игры v=1/Z.

Для определения оптимальной стратегии 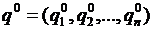игрока В следует учесть, что игрок стремится минимизировать гарантированный выигрыш, т.е. найти max 1/v. Переменные q₁, q₂,…, q_n удовлетворяют неравенствам

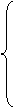a₁₁q₁+ a₁₂q₂+…+ a_1nq_n ≤ v

a₂₁q₁+ a₂₂q₂+…+ a_2nq_n ≤ v

………………………………

a_m1q₁+ a_m2q₂+…+ a_mnq_n ≤ v

Если также как и в предыдущем случае ввести новые переменные:

y₁=q₁/v, y₂=q₂/v, …., y_n=q_n/v,

то предыдущая система примет вид:

a₁₁y₁+ a₁₂y₂+…+ a_1ny_n ≤ 1

a₂₁y₁+ a₂₂y₂+…+ a_2ny_n ≤ 1

……………………………

a_m1y₁+ a_m2y₂+…+ a_mny_n ≤ 1,

а задача сводится к задаче линейного программирования, в которой надо найти максимум целевой функции Z’ = y₁+y₂+…+ y_n при заданных системой ограничениях.

Решение задачи линейного программирования определяет оптимальную стратегию 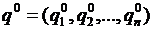. При этом цена игры

v = 1/max Z' = 1/min Z.

Пример . Найти решение игры со следующей платежной матрицей:

С=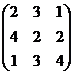

Так как матрица не имеет седловой точки, то ее решение будем искать в смешанных стратегиях. Математические модели будут состоять из пары двойственных задач линейного программирования. Первая задача на нахождение минимума функции F(x) = x₁+ x₂+ x₃

При следующих ограничениях:

2x₁+4x₂+ x₃ ≥ 1

3x₁+2x₂+3x₃ ≥ 1

x₁+2x₂+4x₃ ≥ 1

x_i ≥ 0, i=1,3

где 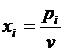, i=1,3

Вторая задача будет на нахождение максимума функции Z(y)=y₁+y₂+y₃

При следующих ограничениях:

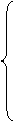2y₁+3y₂+ y₃ ≤ 1

4y₁+2y₂+ 2y₃ ≤ 1

y₁+3y₂+ 4y₃ ≤ 1

y_i ≥ 0, i=1,3

где 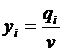, i=1,3

Решение задач может быть выполнено симплекс-методом.

Задачи для самостоятельного решения.

Составив прямую и двойственную задачи линейного программирования решить задачи:

1. 2. 3.

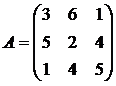
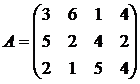
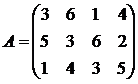
4. 5. 6.

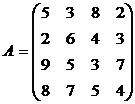
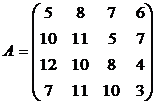
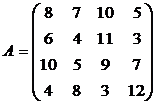
7. 8. 9.

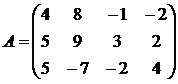
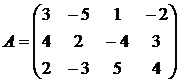
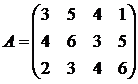
10. 11. 12.