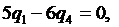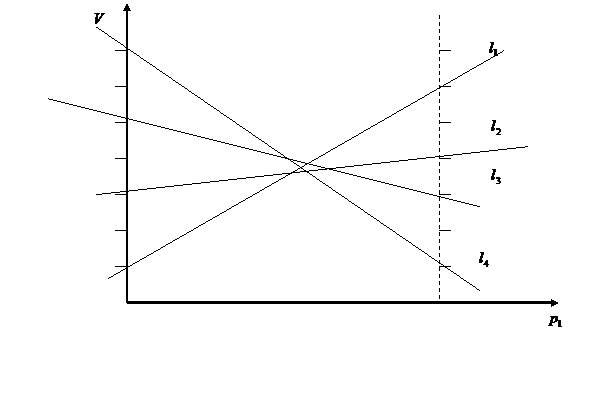Графическое решение игр 2xm или nx2.

Рассмотрим сначала игру, в которой у первого игрока две стратегии, а у второго m стратегий. Тогда платежная матрица будет иметь вид:

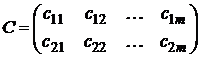
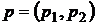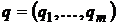Вектор смешанной стратегии первого игрока состоит из двух элементов, а второго – из m элементов, то есть и . Воспользуемся правой частью определения решения игры в смешанных стратегиях. Пусть первый игрок применил свою оптимальную смешанную стратегию, а второй любую, кроме оптимальной (поочередно свои чистые стратегии). Тогда, умножив вектор p на первый столбец матрицы, воспользуемся нормировочным условием, для того, чтобы сделать замену и получим функцию, зависящую от одной переменной:

.

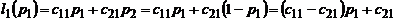Аналогично поступим со всеми остальными столбцами:

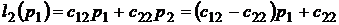и т.д.

Последняя функция привет вид:

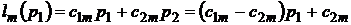
Сначала на плоскости 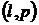последовательно рисуются прямые. Затем для каждого значения 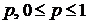, путем визуального сравнения соответствующих ему значений l на каждой из построенных прямых определяется и отмечается минимальное из них. В результате описания процедуры получается ломаная, которая является нижней огибающей. Верхняя точка нижней огибающей определяет и цену игры и оптимальную стратегию.

Объясняется этот выбор просто. Оптимальной стратегией первого игрока является максиминная стратегия и поэтому из всех минимумов он выбирает максимум. Пересечение прямых, дающих точку максимума определяет выигрыш игрока, а номера прямых, которые пересекаются в этой точке соответствуют применению вторым игроком данных стратегий с вероятностью, отличной от нуля. Вероятности применений стратегий второго игрока, которые не участвуют в образовании точки экстремума, равны нулю.

В нашем случае эту точку дают пересечения прямых 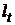и 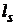. Разность между элементами одного столбца является угловым коэффициентом прямой и обозначим его через k. Тогда:

,

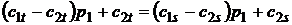или через угловые коэффициенты

,

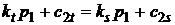откуда просто определяется вероятность применения первым игроком своей первой стратегии: .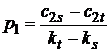

Для того чтобы определить выигрыш, достаточно подставить вероятность в любое равенство, дающее точку экстремума.

Остается определить вероятности применения стратегий вторым игроком. Для этого можно воспользоваться решением игры 2х2, а можно уже найденными угловыми коэффициентами прямых. Рассмотрим игру, составленную из строк и столбцов, вероятности применения которых игроками не равны нулю: .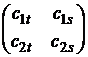

Тогда для определений оптимальной стратегии второго игрока необходимо воспользоваться системой: 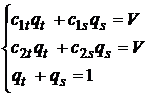. Вычтем из первого равенство второе и сделаем замену переменных 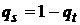и получим: 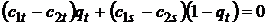, или в угловых коэффициентах 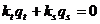. Откуда с помощью элементарных вычислений имеем: 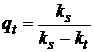, и тогда 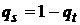будут являться оптимальными смешанными стратегиями второго игрока.

Пример. Рассмотрим игру, заданную матрицей .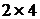

.

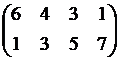Шаг 1. Проверим, имеет ли данная игра решение в чистых стратегиях. Нижняя цена игры равна 1, а верхняя – 4. Седловой точки нет. Следовательно, обязано существовать решение в смешанных стратегиях.

Составим функции для построения графика:

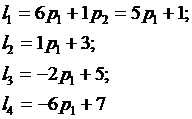
Построим график, где по оси абцисс отложим вероятность 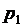, а по оси ординат – выигрыш.

Нас интересует нижняя огибающая и максимальная точка из нее. Это пересечение первой и четвертой прямых. Тогда

, и, следовательно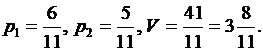

Таким образом, оптимальная смешанная стратегия найдена. Найдем теперь оптимальные смешанные стратегии второго игрока. Так как в точке экстремума активными стратегиями являются первая и четвертая, то уравнение для нахождения оптимальных вероятностей второго игрока имеет вид: