Следствия из принципа максимума

Теорема единственности. Если две функции u₁(x,t) и u₂(x,t), определённые и непрерывные в области 0£t£T и 0£x£l, удовлетворяют уравнению теплопроводности:

u_t=a²u_xx+f(x,t) (для 0<x<l, t>0)

и одинаковым начальным и граничным условиям:

u₁(x,0) = u₂(x,0) = j (x);

u₁(0,t) = u₂(0,t) = m₁(t);

u₁(l,t) = u₂(l,t) = m₂(t),

то тогда u₁(x,t) º u₂(x,t).

Для доказательства этой теоремы рассмотрим функцию:

u(x,t)= u₂(x,t)– u₁(x,t).

Поскольку функции u₁(x,t) и u₂(x,t) непрерывны при 0£t£T; 0£x£l, то и функция u(x,t), равная их разности, также непрерывна в этой же области. Как разность двух решений уравнения теплопроводности в области 0<x<l, t>0 функция u(x,t) является решением однородного уравнения теплопроводности в этой области. Применим к u(x,t) принцип максимума и минимума. На границах по условию задачи имеем:

u(x,0) = 0; u(0,t) = 0; u(l,t) = 0.

Но поскольку и максимум и минимум на границах равны нулю, то и функция будет равна нулю, поэтому u(x,t) º 0. Отсюда u₁(x,t) º u₂(x,t). Таким образом, решение уравнения единственно. Теорема единственности доказана.

Докажем ещё ряд прямых следствий из принципа максимума.

1. Если два решения уравнения теплопроводности u₁(x,t) и u₂(x,t) удовлетворяют условиям:

u₁(x,0)£u₂(x,0); u₁(0,t)£u₂(0,t); u₁(l,t)£ u₂(l,t),

то u₁(x,t) £ u₂(x,t) для всех значений 0£t£T; 0£x£l.

Доказательство. Разность u=u₂–u₁ удовлетворяет условиям, при которых установлен принцип максимального значения, и, кроме того:

u(x,0)³0; u(0,t)³0; u(l,t)³0.

Поэтому u(x,t)³0 для 0<x<l; 0<t£T, т.к. иначе функция u(x,t) имела бы отрицательное минимальное значение в области 0<x<l; 0<t£T.

2. Если три решения уравнения теплопроводности u(x,t); 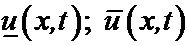удовлетворяют условиям 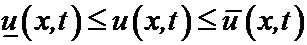при t=0; x=0; x=l, то эти же неравенства выполняются тождественно, т.е. для всех x и t при 0£t<T; 0£x£l.

Это утверждение доказывается применением следствия 1) к функциям: u(x,t), 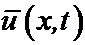и u(x,t), .

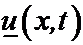3. Если для двух решений уравнения теплопроводности имеет место неравенство:

|u₁(x,t)–u₂(x,t)|£e для t=0; x=0; x=l,

то |u₁(x,t)–u₂(x,t)| £e тождественно, т.е. имеет место для всех t и x, 0£ t< T; 0£ x£ l.

Это утверждение вытекает из следствия 2), если его применить к следующим трём решениям уравнения теплопроводности:

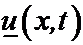=–e

u(x,t) = u₁(x,t)–u₂(x,t)

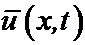=e

Следствие 3) позволяет установить непрерывную зависимость решения первой краевой задачи от начального и граничных условий. Если мы в некоторой физической задаче вместо решения u уравнения теплопроводности, соответствующего начальному и граничным условиям:

u(x,0) =j (x); u(0,t) = m₁(t); u(l,t) = m₂(t),

возьмём решение u*(x,t), соответствующее другим начальному и граничным значениям, определяемым функциями j*(x); m₁*(t); m₂*(t), которые отличаются от предыдущих на e, т.е.

|j(x)– j*(x)| £e; |m₁(t)– m₁*(t)| £e; |m₂(t)– m₂*(t)| £e;

то функция u(x,t) будет отличаться от функции u*(x,t) на то же число e:

| u(x,t)– u*(x,t)| £e.

Это неравенство доказывает непрерывную зависимость решения первой краевой задачи от начального и граничных условий.

Принцип максимума для гармонических функций в R³ и его следствия

Теорема. Если функция q(M) является гармонической внутри связной замкнутой ограниченной области V и непрерывной внутри области и на её границе, то наибольшее и наименьшее значения этой функции могут достигаться только на границе области V (за исключением того случая, когда q(M) постоянна всюду в V).

Напомним, что область V называется связной, если любые две внутренние точки этой области можно соединить непрерывной линией, целиком лежащей внутри области.

Поясним смысл этой теоремы. Так как функция q(M) по условию является непрерывной в замкнутой, ограниченной области V, то она ограничена в этой области и достигает в ней наибольшего и наименьшего значений. Где же находится эта точка M₀, в которой функция достигает, например, наибольшего значения? Докажем, что она не может находиться внутри области, следовательно она находится на границе. Доказательство проводится методом от противного.

Пусть функция q(M) достигает своего наибольшего значения в точке M₀, лежащей внутри области V (см. рис. 29.1). Если M₀ является внутренней точкой области, то вокруг M₀ можно описать шар с центром в точке M₀, целиком принадлежащий V. Обозначим радиус этого шара через r. Тогда по третьему свойству гармонической функции, имеет место равенство:

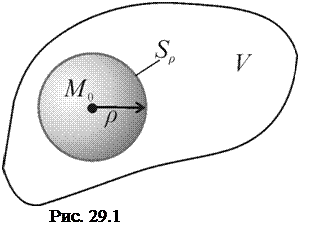
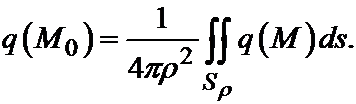Запишем тождество:

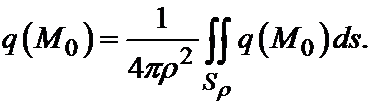Вычитая почленно эти два равенства, получим:

.

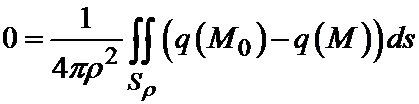Сокращая на 4pr², имеем:

.

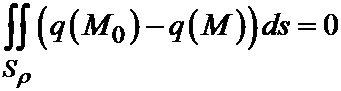Подынтегральная функция здесь непрерывна и неотрицательна т. к. по условию q(M₀) является наибольшим значением функции в области V. Но интеграл от непрерывной, неотрицательной функции может быть равен нулю в том и только в том случае, когда эта функция тождественно равна нулю в области интегрирования. Итак q(M₀)–q(M)=0 или q(M₀)=q(M) всюду на S_r. А так как все эти вычисления можно применить и к сфере любого радиуса, меньшего чем r, то q(M)=q(M₀) всюду внутри шара радиуса r, т.е. в этом шаре функция q всюду постоянна.

Докажем теперь, что если внутренняя точка M₀ является точкой наибольшего значения в области V, то функция будет постоянной не только в окрестности точки M₀, но и всюду внутри области V.

r

Возьмём для этого произвольную точку M₁ внутри области V и соединим её с точкой M₀ непрерывной кривой l, лежащей внутри этой области (что можно сделать в силу связности области V (см. рис. 29.2)).

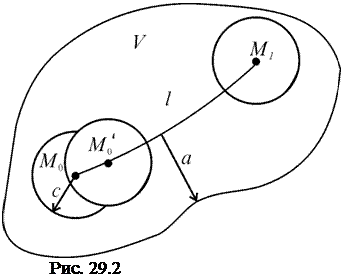
Пусть a>0 – наименьшее расстояние между точками этой кривой и точками границы области V. Опишем вокруг M₀ шар радиуса r, где r – какое-либо число, меньшее, чем a, поэтому он будет лежать внутри области V. По доказанному чуть выше внутри этого шара функция постоянна. Сместим теперь центр шара вдоль по кривой l так, чтобы новый центр 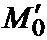не вышел за пределы ранее построенного шара. Тогда и внутри нового шара функция всюду принимает постоянное значение, равное q(M₀). (Это следует из того, что в точке 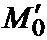функция принимает наибольшее в области V значение, т.к. .

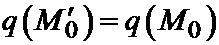Перемещая таким образом центр шара всё дальше, совместим его, в конце концов, с точкой M₁. Рассуждая также как и при переходе от точки M₀ к точке 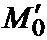, убедимся, что значение функции во всех точках кривой l одно и то же: в частности q(M₁)=q(M₀).

Итак, если бы гармоническая функция достигала наибольшего значения внутри области V, то эта функция принимала бы во всех внутренних точках области одно и то же значение; в силу непрерывности, она должна была бы принимать это же значение и на границе области; иными словами, эта функция была бы постоянной в области V.

Следовательно, если гармоническая функция не постоянна, то она не может достигать наибольшего значения внутри области V. Значит, точка, в которой функция достигает своего наибольшего в области V значения, находится на границе этой области.

Аналогично доказывается, что для непостоянной гармонической функции точка, где функция достигает своего наименьшего значения, также находится на границе области V.

Замечание. Частным случаем гармонической функции является линейная функция q=Ax+By+Cz+D. Для неё доказанное свойство совершенно очевидно. Поверхностями уровня для такой функции являются параллельные плоскости: Ax+By+Cz+D= const. Если точка M₀ является внутренней точкой области V, то на плоскостях уровня, лежащих по одну сторону от точки M₀, функция принимает значения, меньшие, чем q(M₀), а на плоскостях, лежащих по другую сторону – большие, чем q(M₀) (см. рис. 29.3). Но это значит, что точка M₀ не является ни точкой наибольшего ни точкой наименьшего значений функции q(M).

Следствия из теоремы о наибольшем и наименьшем значениях гармонической функции.

Следствие 1. Если функции u и U непрерывны в области V+S, гармоничны в V и если u£ U на S, то u£ U всюду внутри V.

Доказательство. В самом деле, функция U–u непрерывна в V+S, гармонична в V и U–u ³ 0 на S. В силу принципа максимального значения U–u ³ 0 всюду внутри V, откуда следует, что u£U. Что и требовалось доказать.

Следствие 2. Если функции u и U непрерывны в области V+S, гармоничны в V и если |u| £ U на S, то |u| £ U всюду внутри V.

Доказательство. Из условий теоремы о наибольшем и наименьшем значениях следует, что три гармонические функции –U, u и U удовлетворяют условиям:

–U £ u £ U на S.

Применяя дважды следствие 1, получим, что –U £ u £ U всюду внутри V, или |u|£ U внутри V.

Следствие 3. Если для гармонической в V и непрерывной в V+S функции и выполняется неравенство 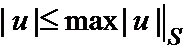, то оно выполняется всюду в V.

Для доказательства положим 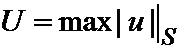и воспользуемся следствием 2.