Применение дифференциала в приближенных вычислениях значений функций

НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

СОДЕРЖАНИЕ

Введение……………………………………………………

1. Частные производные. ……………………………………………………

Указания к задаче 1……………………………………………………

1. Производные неявной функции……………………………………………

Указания к задаче 2……………………………………………………

1. Дифференциал……………………………………………

Указания к задаче 3……………………………………………………

1. Применение дифференциала в приближенных вычислениях значений функций……………………………………………

Указания к задаче 4……………………………………………………

1. Формулы Тейлора и Маклорена…………………

Указания к задаче 5……………………………………………………

1. Касательная плоскость и нормаль к поверхности…………………

Указания к задаче 6……………………………………………………

1. Градиент и производная по направлению…………………

Указания к задаче 7……………………………………………………

1. Экстремум функции нескольких переменных …………………

Указания к задаче 8……………………………………………………

Указания к задаче 9……………………………………………………

1. Условный экстремум функции нескольких переменных…………………

Указания к задаче 10……………………………………………………

1. Наименьшее и наибольшее значение функции…………………

Указания к задаче 11……………………………………………………

1. Метод наименьших квадратов……………………………………

Указания к задаче 12……………………………………………………

Указания к задаче 13……………………………………………………

1. Расчетные задания………………………………………………

Список литературы…………………………………………………………

Частные производные

Пусть 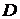- множество пар 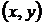значений независимых переменных 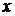и .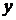

Определение.Если каждой паре 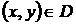поставлено в соответствие некоторое значение переменной величины 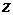, то говорят, что 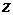- функция двух независимых переменных 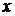и 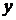, определенная на множестве 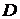. Множество 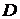называется областью определения функции .

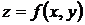Определение.Если каждой совокупности 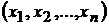значений независимых переменных 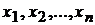из некоторого множества 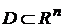соответствует определенное значение переменной 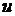, то говорят, что 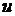- функция 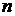переменных, определенная на множестве ( ).

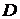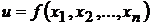Определение.Частной производной функции 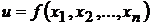по переменной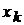 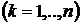в точке 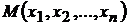называется предел (если он существует)

.

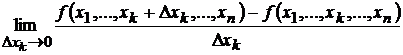Обозначается 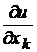или .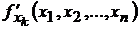

Для функции 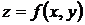двух переменных по определению имеем

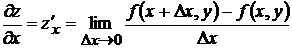- частная производная по ,

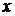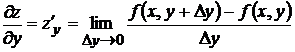- частная производная по .

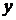Замечание. Частные производные вычисляются по обычным правилам и формулам дифференцирования (при этом все переменные, кроме 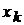, рассматриваются как постоянные).

Определение.Частными производными 2-го порядка функции 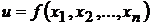называются частные производные от ее частных производных первого порядка.

Производные второго порядка обозначаются следующим образом:

,

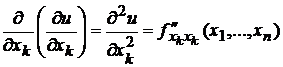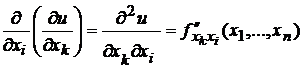и т.д.

Аналогично определяются и обозначаются частные производные порядка выше второго.

Замечание. Результат многократного дифференцирования функции по различным переменным не зависит от очередности дифференцирования при условии, что возникающие при этом смешанные частные производные непрерывны.

Указания к задаче 1.

Дана функция 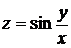. Показать, что .

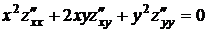Решение. Найдем частные производные

; ;

;

;

.

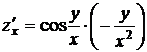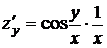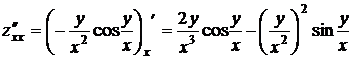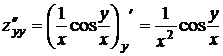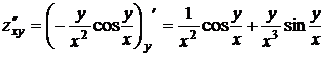Подставляя найденные частные производные в левую часть данного уравнения, получим тождество

,

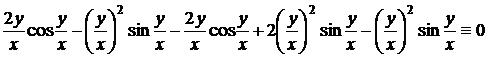что и требовалось доказать.

Производные неявной функции

Частные производные неявной функции 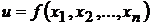, заданной с помощью уравнения 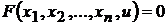, вычисляются по формулам

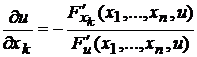
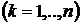, (2.1)

при условии, что .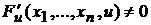

Производная неявной функции 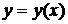, заданной с помощью уравнения 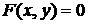, может быть вычислена по формуле:

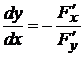при условии, что 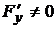. (2.2)

Указания к задаче 2.

2.1. Найти первые производные неявной функции, заданной уравнением .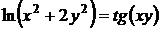

Решение. Производная неявной функции 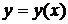, заданной с помощью уравнения 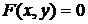, может быть вычислена по формуле (2.2): 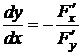при условии, что .

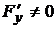В данном случае . , .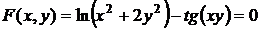

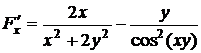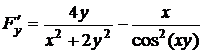Найдем производную неявной функции:

.

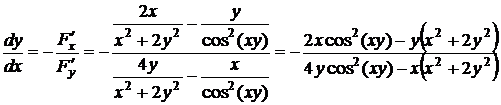2.2. Найти первые производные неявной функции, заданной уравнением .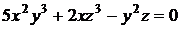

Решение. Производные неявной функции 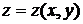, заданной с помощью уравнения 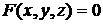, могут быть вычислены по формуле (2.1): 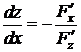, 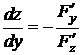при условии, что .

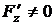В данном случае , , , .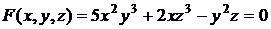

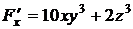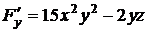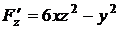Найдем производные неявной функции:

, .

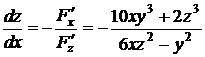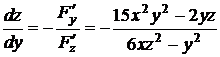Дифференциал

Определение.Полным приращением функции 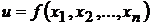в точке 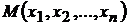, соответствующим приращениям аргументов 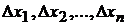называется разность .

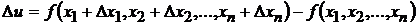Определение.Функция 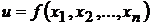называется дифференцируемой в точке 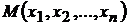, если в некоторой окрестности этой точки полное приращение функции может быть представлено в виде

,

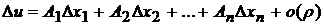где 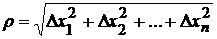, 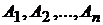- числа, не зависящие от .

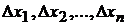Определение.Дифференциалом 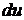первого порядка функции 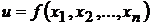в точке 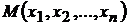называется главная часть полного приращения этой функции в рассматриваемой точке

.

.

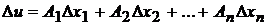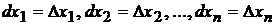Для дифференциала функции 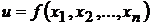справедлива формула

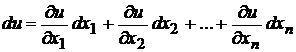. (3.1)

Для функции 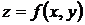двух переменных имеем

.

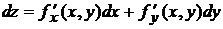Дифференциал 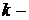го порядка функции 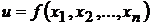выражается символической формулой

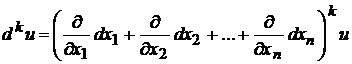. (3.2)

Например, в случае функции 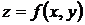двух переменных для дифференциалов 2-го и 3-го порядков справедливы формулы

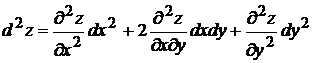, (3.3)

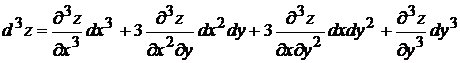. (3.4)

Указания к задаче 3.

3.1. Найти дифференциал третьего порядка 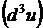функции .

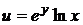Решение. Найдем все частные производные до третьего порядка включительно:

, ,

, ,

, , , .

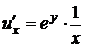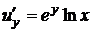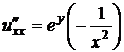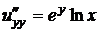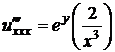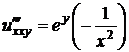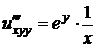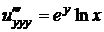Найдем дифференциал третьего порядка функции 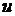двух переменных по формуле (3.4):

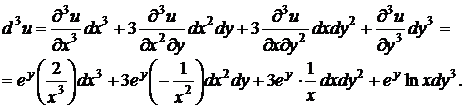
3.2.Найти дифференциал второго порядка 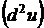функции .

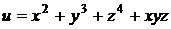Решение. Для нахождения дифференциала второго порядка функции трех переменных воспользуемся формулой (3.2):

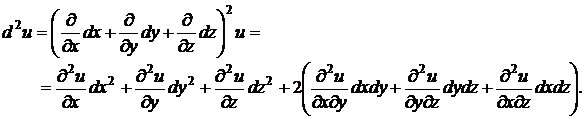
Найдем все частные производные до второго порядка включительно:

, , ,

, , ,

, , .

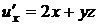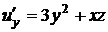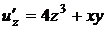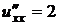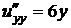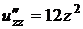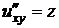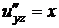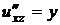Найдем дифференциал второго порядка функции 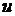трех переменных:

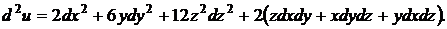
Указания к задаче 4.

Вычислить приближенное значение функции 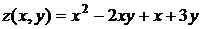в точке А(3,94; 2,01).

Решение. Приближенное значение функции 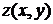в точке А вычислим, используя формулу (4.1):

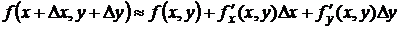
или .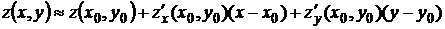

Вычислим значение функции в точке с координатами 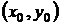. Если 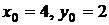, то .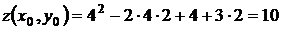

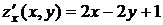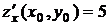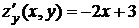Так как , то ,

, то .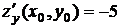

Подставим в формулу: .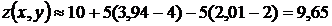

Формулы Тейлора и Маклорена

Для функции 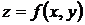двух переменных формула Тейлора имеет вид

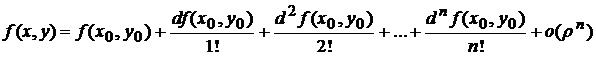, (5.1)

где 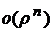- остаточный член .

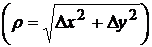В частном случае, при 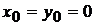, формула (5.1) называется формулой Маклорена.

Указания к задаче 5.

Разложить функцию 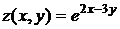в окрестности точки М(2,1), ограничиваясь членами второго порядка включительно

Решение. В данном случае формула Тейлора (5.1) принимает вид 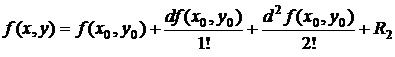, где 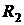- дополнительный член формулы Тейлора.

Найдем значения всех частных производных функции до второго порядка включительно в точке М:

, , , , .

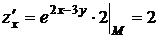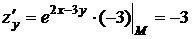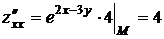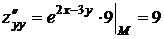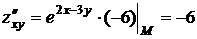Составим дифференциалы функции до второго порядка включительно

,

.

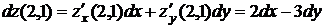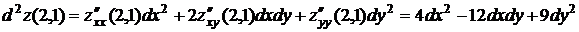Учитывая, что 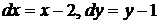, получим:

.

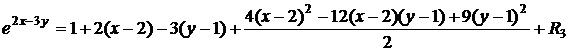Указания к задаче 6.

6.1. Составить уравнение касательной плоскости и уравнения нормали к поверхности 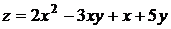в точке А(1,2,7).

Решение. Если уравнение поверхности задано в явной форме 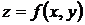, то уравнение касательной плоскости в точке 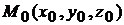имеет вид (6.1)

,

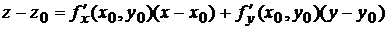а уравнение нормали (6.2) –

.

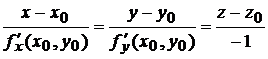Найдем значения частных производных 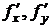в точке М:

, .

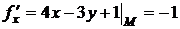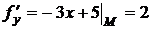Подставляя найденные значения в уравнения касательной плоскости и нормали, получим

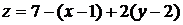или 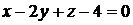- уравнение касательной плоскости, 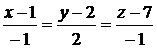- уравнение нормали.

6.2. Составить уравнение касательной плоскости и уравнения нормали к поверхности 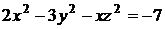в точке А(1,0,3).

Решение. Если уравнение поверхности задано в неявной форме 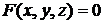, то уравнение касательной плоскости в точке 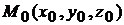имеет вид (6.3)

.

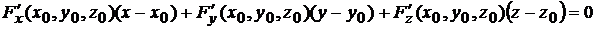Уравнение нормали (6.4)

.

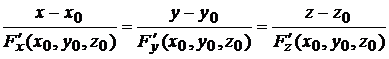Найдем значения частных производных 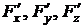в точке М:

, , .

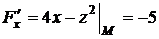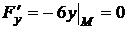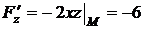Подставляя найденные значения в уравнения касательной плоскости и нормали, получим

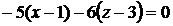или 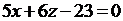- уравнение касательной плоскости, 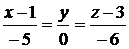- уравнение нормали.

Указания к задаче 7.

Даны: функция 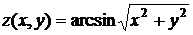,точка 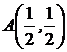и вектор .

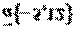Найти: 1) 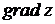в точке А;

2) производную в точке А по направлению вектора .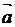

Решение.

Найдем 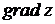в точке А , для этого вычислим 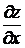и 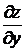в точке А. Имеем:

,

.

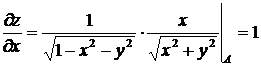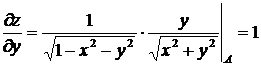Таким образом, .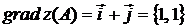

Для нахождения производной функции 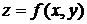в направлении вектора 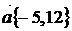воспользуемсяформулой (7.1). Для этого найдем единичный вектор 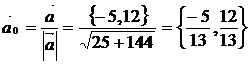, тогда

.

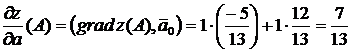8. Экстремум функции нескольких переменных

Пусть функция 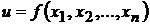определена в некоторой окрестности точки .

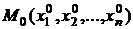Определение.Функция 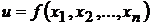имеет максимум (минимум) в точке 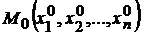, если существует такая окрестность точки 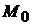, в которой для всех точек 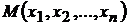( 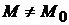) выполняется неравенство 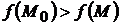(соответственно ).

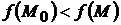Максимум или минимум функции называется ее экстремумом, а точки, в которых функция имеет экстремум, называются точками экстремума (максимума или минимума).

Необходимое условие экстремума.Если функция 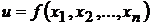имеет экстремум в точке 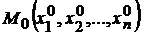, то в этой точке

.

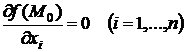Точки, в которых выполняются эти условия, называются стационарными точками функции .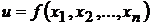

Достаточное условие экстремума.Пусть 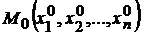- стационарная точка функции 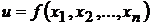, причем эта функция дважды дифференцируема в некоторой окрестности точки 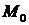и все ее вторые частные производные непрерывны в точке 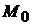. Тогда:

если второй дифференциал 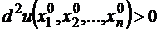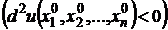при любых значениях 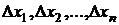, не равных одновременно нулю, то функция 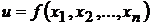имеет в точке 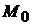минимум (максимум);

если 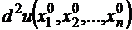принимает значения разных знаков в зависимости от 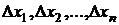, то экстремума в точке 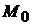нет;

если 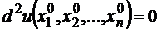для набора значений 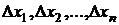, не равных нулю одновременно, то требуются дополнительные исследования.

Рассмотрим случай функции двух переменных.

Определение. Функция 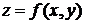имеет максимум (минимум) в точке 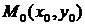, если существует такая окрестность точки 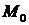, в которой для всех точек 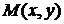отличных от 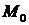, выполняется неравенство .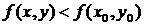

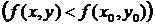Необходимое условие экстремума функции двух переменных. Если дифференцируемая функция 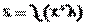достигает экстремума в точке 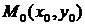, то в этой точке частные производные первого порядка равны нулю, т.е.

,

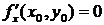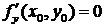. (8.1)

Введем обозначения:

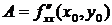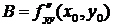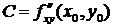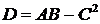, , , . (8.2)

Достаточное условие экстремума функции двух переменных.Пусть 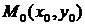- стационарная точка функции 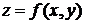и пусть в окрестности точки 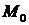функция имеет непрерывные частные производные второго порядка. Тогда:

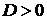если , то функция 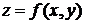имеет в точке 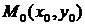экстремум, а именно максимум при 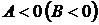и минимум при ;

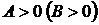если 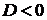, то экстремум в точке 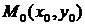отсутствует;

если 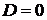, то требуются дополнительные исследования.

Рассмотрим случай функции 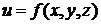трех переменных.

Критерий Сильвестра. 1) Для того, чтобы выполнялось неравенство 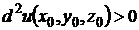при любых значениях 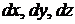, не равных нулю одновременно, необходимо и достаточно, чтобы:

, , .

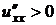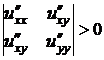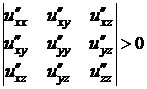2) Для того, чтобы выполнялось неравенство 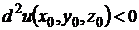при любых значениях 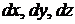, не равных нулю одновременно, необходимо и достаточно, чтобы:

, , .

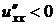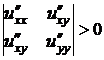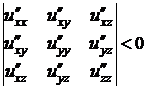Следует помнить, что все производные здесь вычислены в точке .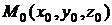

Указания к задаче 8.

Найти экстремумы функции двух переменных .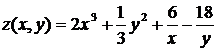

Решение.

По необходимому условию экстремума, если дифференцируемая функция 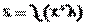достигает экстремума в точке 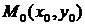, то в этой точке частные производные первого порядка равны нулю.

Найдем стационарные точки функции :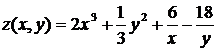

, .

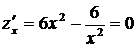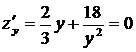Решая данную систему, получаем две стационарные точки 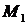(1,-3), 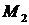(-1,-3).

Воспользуемся достаточным условием экстремума функции двух переменных. По формулам (8.2) найдем , , , .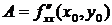

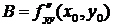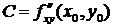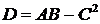Рассмотрим точку 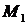(1,-3): 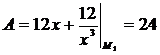, , 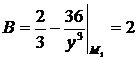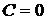. Так как 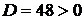, то точка 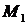(1,-3) является точкой экстремума, а именно минимума, так как 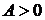. Найдем минимум функции: .

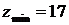Рассмотрим точку 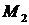(-1,-3): 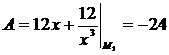, , 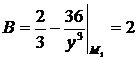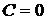. Так как 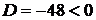, то в точке 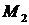(-1,-3) экстремума нет.

Условный экстремум

Пусть требуется найти экстремум функции 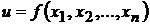при условии, что 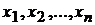связаны уравнением

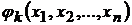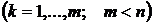, . (9.1)

Уравнения (9.1) называются уравнениями связи.

Определение.Функция 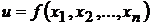имеет условный максимум (условный минимум) в точке 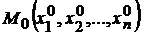, если существует такая окрестность точки 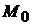, в которой для всех точек 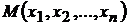( 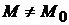), удовлетворяющих уравнениям связи, выполняется неравенство 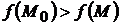(соответственно ).

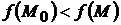Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа

,

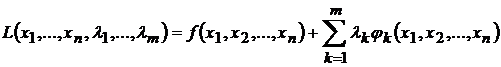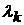
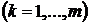называются множителями Лагранжа.

Необходимое условие условного экстремума.Если функция 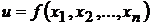имеет условный экстремум в точке 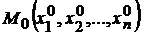, то в этой точке

.

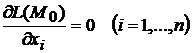Для нахождения точки, в которой возможен условный экстремум, составим систему 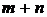уравнений:

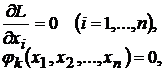, (9.2)

из которой найдем неизвестные , .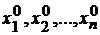

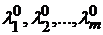Достаточное условие условного экстремума.Пусть 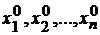, 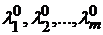решения системы (9.2), удовлетворяющие уравнениям 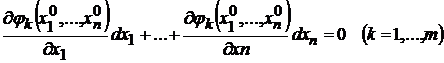при 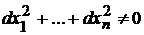. Функция 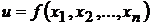имеет в точке 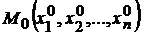условный максимум, если

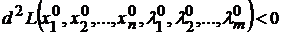
и условный минимум, если

.

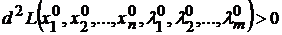В случае функции 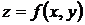двух переменных при уравнении связи 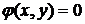функция Лагранжа примет вид

.

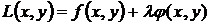Система (9.2) запишется в виде

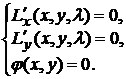
Пусть 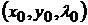- любое из решений этой системы и

.

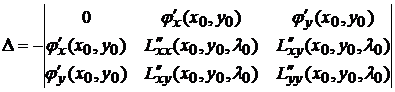Тогда, если 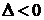, то функция имеет в точке 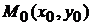условный максимум; если 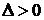– условный минимум.

Указания к задаче 11.

Найти наименьшее и наибольшее значения функции 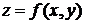в ограниченной замкнутой области 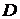, заданной системой неравенств.

, .

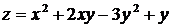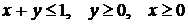Решение.

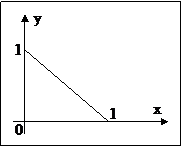Область представляет собой треугольник, ограниченный координатными осями и прямой .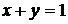

1) Найдем стационарные точки функции внутри области 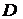. В этих точках частные производные равны нулю:

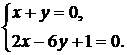
Решая данную систему, получим точку 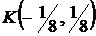. Эта точка не принадлежит области 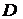, следовательно, в области 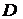стационарных точек не имеем.

2) Исследуем функцию на границе области. Поскольку граница состоит из трех участков, описываемых тремя различными уравнениями, то будем исследовать функцию на каждом участке отдельно:

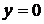· . На этом участке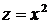 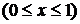. Так как 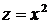- возрастающая функция переменно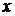й при 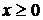, то на отрезке 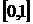наименьшее значение функции 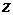будет в точке (0,0): 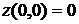, а наибольшее – в точке (1,0): .

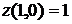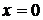· . На этом участке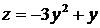 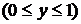. Найдем производную 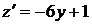. Из уравнения 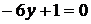получаем 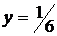. Таким образом, наибольшее и наименьшее значения функции 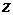на границе 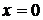находятся среди ее значений в точках (0,0), (0,1), 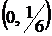. Найдем эти значения: , .

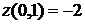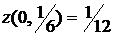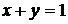· или 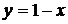, 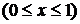. На этом участке 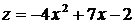. Решая уравнение 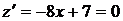, получим 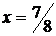, следовательно, 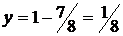. Значение функции в этой точке равно 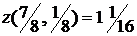, а на концах отрезка 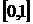значение функции найдены выше.

3) Сравнивая полученные значения 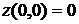, , 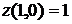, , 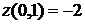, 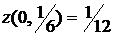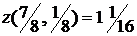заключаем, что наибольшее и наименьшее значения функции в замкнутой области 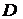равны соответственно 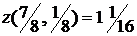и .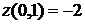

11. Метод наименьших квадратов

В различных исследованиях на основании эксперимента требуется установить аналитическую зависимость 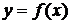между двумя переменными величинам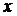и и 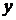. Широко распространенным методом решения этой задачи является метод наименьших квадратов.

Пусть в результате эксперимента получено 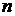значений функции 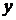при соответствующих значениях аргумента 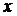. Результаты сведены в таблицу

			…
			…

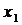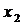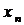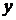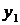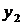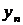Вид аппроксимирующей функции 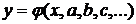устанавливается или из теоретических соображений, или на основании характера расположения на плоскости точек, соответствующих экспериментальным значениям.

При выбранном виде функции остается подобрать входящие в нее параметры 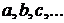так, чтобы в каком-то смысле она наилучшим образом описывала рассматриваемый процесс.

Метод наименьших квадратов заключается в следующем. Рассмотрим сумму квадратов разностей значений 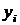, даваемых экспериментом, и функции 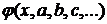в соответствующих точках:

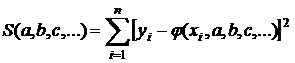. (11.1)

Подбираем параметры 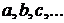так, чтобы эта сумма имела наименьшее значение. Таким образом, задача свелась к исследованию функции 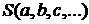на экстремум.

Из необходимого условия экстремума функции нескольких переменных следует, что эти значения 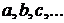удовлетворяют системе уравнений

.

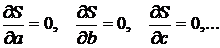Или в развернутом виде

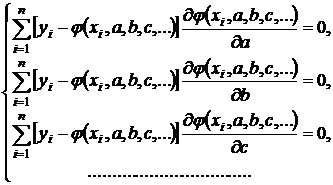(11.2)

Если требуется найти функцию вида 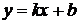, то функция 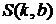в этом случае имеет вид

.

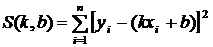Это функция с двумя переменным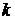и и 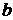. Исследуем ее на экстремум. Запишем необходимые условия экстремума:

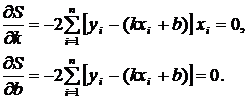
Отсюда получаем следующую систему уравнений относительно неизвестных 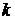и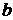

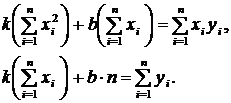(11.3)

Можно показать, что система (11.3) имеет единственное решение, и при найденных значениях 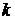и 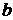функция