Уравнение прямой, проходящей через данную точку параллельно данному вектору

Дано: М₀(х₀;у₀), 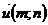, причем .

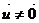Составить уравнение l / l 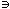М₀, l || /

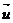Решение.

Определение 1.

Вектор, отличный от нулевого, параллельный искомой прямой, называется направляющим вектором прямой.

Точка плоскости М принадлежит прямой l, если координаты точки удовлетворяют уравнению прямой. На языке векторов это означает, что, где бы ни лежала точка М на прямой l, вектор 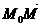коллинеарен вектору .

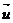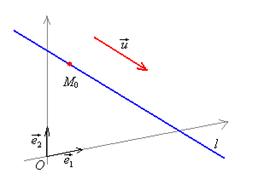
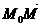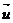|| , или,

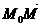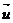=t . (12.4)

Откуда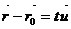

Получили векторное уравнение прямой: 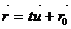(12.5)

Откуда 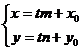(12.6)

– параметрические уравнения прямой, где t – параметр.

Условие коллинеарности векторов: координаты 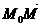, 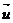пропорциональны. Если 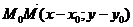, , 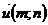то.

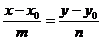(12.7)

Это уравнение связывает координаты точки М₀, вектора 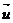и произвольной точки М прямой l. Оно называется каноническим уравнением прямой.

Условие коллинеарности векторов 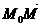, 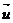можно записать в форме определителя, используя свойство: определитель с пропорциональными строками равен нулю, т.е.

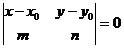(12.8)

Это уравнение прямой в форме определителя. Откуда

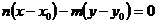, (12.9)

Коэффициенты m и n одновременно не обращаются в нуль, т.к. 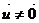. Из уравнения (12.9) вытекают следствия:

1. Если l || 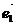(1;0) , то уравнение примет вид 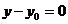(прямая параллельна оси Ох).

2. Если l || 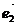(0;1) , то уравнение примет вид 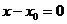(прямая параллельна оси Оу).

3. Если прямая не параллельная осям, тогда выразим :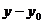

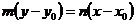
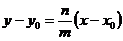, (12.10)

где 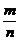– угловой коэффициент прямой в данной системе координат.

Уравнение прямой, проходящей через две точки

Дано: М₁(х₁;у₁), М₂(х₂;у₂).

Составить уравнение l / l 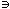М₁, М₂

Решение.

Воспользуемся уравнением прямой, проходящей через данную точку параллельно данному вектору. Возьмем в качестве данной точку М₁(х₁;у₁), а направляющего вектор .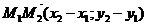

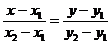(12.11)

Это уравнение прямой, проходящей через две точки.

Общее уравнение прямой

Раскроем определить (12.8):

.

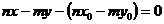Введем обозначения: n=A, –m=B, 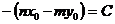. Получим уравнение:

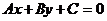(12.12)

Следствие. Так как 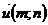, то 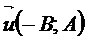. (12.13)

Определение 2.

Уравнение 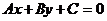называется общим уравнением прямой.

Исследование общего уравнения прямой

o Ах+Ву+С=0, где А, В одновременно не равны нулю, т.е. А²+В²¹0

Возможны следующие частные случаи:

o Один коэффициент равен нулю

o Два коэффициента равны нулю

	Коэффициенты А, В, С	Уравнение Ах+Ву+С=0	Особенность	Рисунок
	С=0	Ах+Ву=0	Точка О (0;0) принадлежит прямой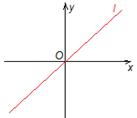
	А=0	Ву+С=0, т.е.	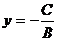Прямая параллельна оси Ох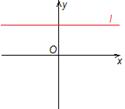
	В=0
	А=С=0	Ву=0, т.е. у=0	Ось Ох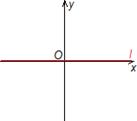
	В=С=0

Пример 1. Составим каноническое, параметрические, общее, нормальное уравнения прямой АВ, если А(1;–2), В(0;5).

Решение. Прямая АВ проходит через две точки, значит, 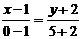. Тогда

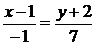– каноническое уравнение прямой АВ,

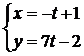– параметрические уравнения прямой АВ,

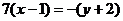, откуда 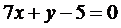– общее уравнение прямой АВ.

Уравнения прямой

В прямоугольной декартовой системе координат

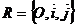
Уравнение прямой, проходящей через точку перпендикулярно вектору

Определение 3.

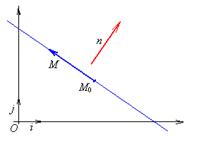Вектор, перпендикулярный (ортогональный) прямой, называется нормальным вектором прямой или вектором нормали.

Дано: 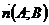, М₀(х;у).

Составить уравнение прямой l / М₀Îl , l^ .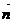

Решение.

Пусть М – точка произвольная прямой l. Рассмотрим векторы 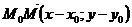и 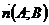. 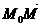– направляющий вектор прямой, 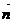– перпендикулярный к ней вектор. Тогда 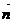^ 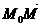, т.е. 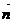× 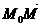=0 (1),

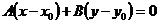(12.14)

Это уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Таким образом, геометрический смысл общего уравнения прямой Ах+Ву+С=0 заключается в том, что коэффициенты А,В – суть координаты векторов:

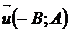– направляющий вектор. (12.15)

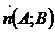– перпендикулярный вектор. (12.16)