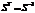Собственные векторы и собственные значения линейного оператора, собственные значения линейного оператора, относящиеся к различным собственным значениям

Ln-ЛВП

Число λ принадлежащее R называется собственным числом(значением) линейного оператора φ, если найдется такой вектор x принадлежащий Ln, что выполняется:

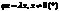
λ - собственное число

х – собственный вектор, соответствующий собственному числу λ.

Введем базис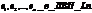

Тогда матрица линейного оператора φ

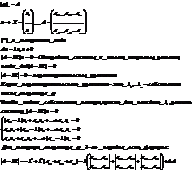
Собственные свойства собственных векторов линейного оператора:

1)Собственные векторы, отвечающие различным собственным значениям линейного оператора, линейно независимы

2)В базисе из собственных векторов матрица линейного оператора имеет диагональный вид, причем на диагонали стоят собственные числа.

Действительно, пусть линейный оператор φ имеет n линейно независимых собственных векторов 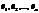,отвечающие собственным числам λ1,… λn.

Выбираем собственные векторы 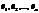в качестве базиса. Чтобы получить матрицу 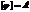нужно найти образы базисных векторов:

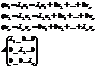
Оператор, матрица которого приводится к диагональному виду, называется оператором простой структуры.

Оператор имеет простую структуру в 2-х случаях:

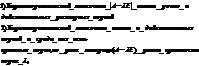
Замечание!!!

Оказывается, все собственные числа оператора, имеющего в ортонормированном базисе симметричную матрицу, действительные числа.

Билет№30

Понятие Евклидова пространства, существование ортонормированного базиса.

Вещественное линейное пространство наз. Евклидовым, если в нем каждой паре векторов(элемент линейного пространства) x,y поставлено в соответствие число (х,у), называемое скалярным произведением векторов х и у, для которого выполняются следующие условия:

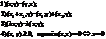
Таким образом, можно говорить об аксиомах евклидового пространства: они включают в себя 8 аксиом линейного пространства и 4 свойства скалярного произведения.

Нормой в линейном пространстве L называется функция, ставящая в соответствии каждому вектору 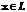вещественное число ||x||, для которого выполняются след. Условия:

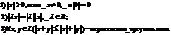В евклидовом пространстве Е ному можно задать следующим образом: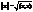

Ортогональный базис евклидова пространства, вектора которого нормированы, т.е. имеют единичную норму, называется ортонормированным.

Билет№31

Квадратичные формы, преобразование матрицы квадратичной формы при переходе к новому базису.

Квадратичной формой n переменных 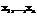называется однородный многочлен второй степени относительно этих переменных:

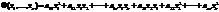* , или в матричном виде 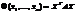, где

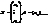
На самом деле квадратичную форму следует рассматривать как функцию, сопоставляющую каждому элементу Хевклидова пространства 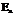некоторое вещественное число 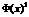. Тогда Ф в * есть ни что иное как функция от координат вектора Х.

Заметим, что матрица А, называемая матрицей квадратичной формы Ф, всегда симметрична, поскольку мы всегда можем потребовать, чтобы 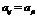, так как это коэффициенты при равных произведениях 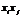и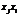

Но поскольку в записи (*) используются координаты вектора, то эта запись зависит от выбранного базиса, и, следовательно, от базиса зависит также и матрица квадратичной формы. Пусть {e} и {e’}-два базиса En, А-матрица квадратичной формы Фв базисе {e}, а А’-в базисе {e’}.Тогда (**)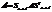

Две квадратичные формы называются эквивалентными, если одна из них переводится в другую посредством невырожденного линейного преобразования координат. Поскольку при невырожденном линейном преобразовании базис переходит в базис, то матрицы двух эквивалентных квадратичных форм будут связаны соотношением вида:(**)

Каноническим видом квадратичной формы называется эквивалентная ей квадратичная форма, содержащая только квадраты переменных: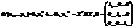

Таким образом, матрица квадратичной формы в каноническом виде диагональная. Базис, в котором квадратичная форма принимает канонический вид, называется каноническим.

Билет№32

Теорема:

Матрица линейного оператора в базисе из собственных векторов имеет диагональный вид, причем не ее диагонали стоят собственные числа оператора.

Билет№33

Матрица А называется ортогональной, если А^Т *А=А*А^Т =Е

Матрица А ортогонального оператора в некотором ортонормированном базисе называется также ортогональнойи обладает тем характеристическим свойством, что ее обратная матрица совпадает с ее транспонированной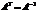

Пример:

Пусть {e},{e’} – ортонормированные базисы в евклидовом пространстве Е, 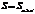Тогда по определению матрицы перехода строки матрицы S(и столбцы 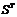)состоят их координат векторов из {e} в базисе {e’}. Докажем, что S – ортогональна, то есть 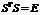, поскольку {e},{e’} – ортонормированны, то

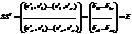
То есть