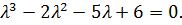Собственные векторы и собственные значения линейного преобразования
В теории автоматического управления собственные значения часто называют характеристическими числами, а собственные векторы – характеристическими векторами. Это очень важные понятия, т.к. собственные значения системы определяют её динамические свойства (устойчивость, быстродействие и др.)
Для введения указанных определений обратимся к векторно-матричному уравнению (3.12). Поставим вопрос, существует ли вектор 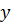 , который имеет такое же направление в векторном пространстве, как и вектор
, который имеет такое же направление в векторном пространстве, как и вектор 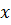 . Если такой вектор существует, то
. Если такой вектор существует, то 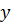 должен быть пропорционален
должен быть пропорционален 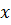 , т.е.
, т.е.
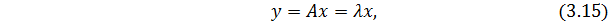
где 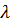 - коэффициент пропорциональности (скаляр).
- коэффициент пропорциональности (скаляр).
Эта задача известна как задача о характеристических числах. Значение 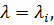 для которого уравнение (3.15) имеет решение
для которого уравнение (3.15) имеет решение 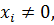 называется характеристическим числом матрицы преобразования
называется характеристическим числом матрицы преобразования 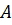 . Соответствующий вектор решения
. Соответствующий вектор решения 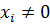 называется собственным (характеристическим) вектором матрицы
называется собственным (характеристическим) вектором матрицы 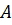 .
.
Соотношение (3.15) можно переписать в виде однородного уравнения
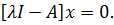 (3.16)
(3.16)
Данное уравнение имеет решение только в том случае, когда
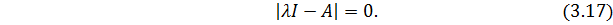
Если раскрыть определитель, то получим так называемое характеристическое уравнение
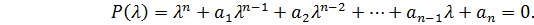 (3.18)
(3.18)
Корни характеристического уравнения равны собственным значениям матрицы A. Они могут быть как действительными, так и комплексными.
Особый интерес представляет коэффициенты характеристического уравнения (3.18) 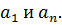 С целью их оценки перепишем (3.18) в виде произведения сомножителей.
С целью их оценки перепишем (3.18) в виде произведения сомножителей.
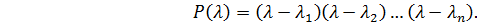 (3.19)
(3.19)
и подставим значение 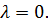 В итоге получим
В итоге получим
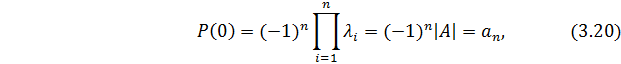
т.е. произведение характеристических чисел равно определителю матрицы 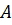 .
.
Коэффициент 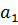 можно получить раскрывая (3.19) и определитель (3.17) и приравнивая коэффициенты характеристических уравнений при
можно получить раскрывая (3.19) и определитель (3.17) и приравнивая коэффициенты характеристических уравнений при 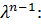
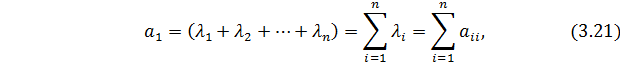 т.е. сумма собственных значений квадратной матрицы равна сумме её диагональных элементов. Последняя получила особое название – след матрицы:
т.е. сумма собственных значений квадратной матрицы равна сумме её диагональных элементов. Последняя получила особое название – след матрицы:
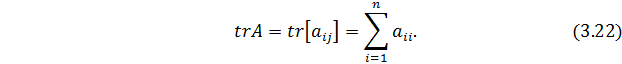
Покажем справедливость соотношений (3.20) и (3.21) на основе примера квадратной матрицы 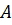 размером 2*2:
размером 2*2:
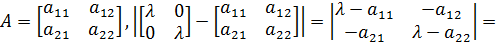
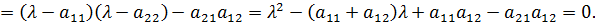
С другой стороны
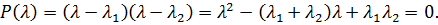
Отсюда 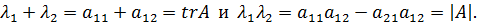
Понятие следа матрицы использовано в алгоритме Бохера, который применяют для получения коэффициентов характеристического уравнения (3.18). Обозначив след матрицы 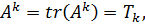 алгоритм Бохера можно представить в виде следующей итерационной процедуры:
алгоритм Бохера можно представить в виде следующей итерационной процедуры:
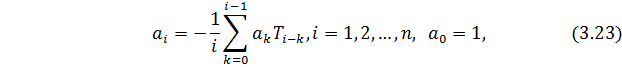
или в развёрнутой форме:
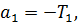
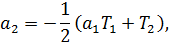
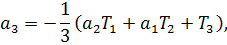
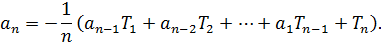
Пример 3.9. Найти характеристическое уравнение матрицы
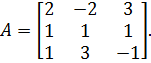
Использование алгоритма (3.23) при n = 3 требует вычисления трёх следов
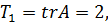
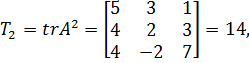
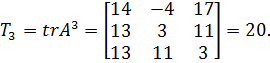
Далее в соответствии с формулой Бохера имеем:
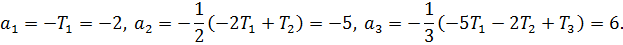
Отсюда характеристическое уравнение равно