ЛНУ с постоянными коэффициентами, метод подбора частного решения.
(1) y(n)+a1y(n-1)+…+any=f(x) – ЛНУ с пост. коэффициентами
L[y]=f(x); yон=yчн+yоо;
Метод подбора частного решения подходит для уравнений со специальной правой частью (f(x)). Она должна подходить под специальный шаблон:
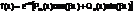 , где α, β – действительные числа, Pm(x), Qn(x) – многочлены степеней m и n с действительными коэффициентами
, где α, β – действительные числа, Pm(x), Qn(x) – многочлены степеней m и n с действительными коэффициентами
Если f(x) подходит под данный шаблон, то решение будет иметь вид:
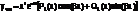 , где r-показатель кратности корня α+βi характеристического многочлена соответствующего однородного уравнения (r=0, если α+βi не является корнем этого многочлена). L=max(m,n)
, где r-показатель кратности корня α+βi характеристического многочлена соответствующего однородного уравнения (r=0, если α+βi не является корнем этого многочлена). L=max(m,n)
PL(x), QL(x) – полные многочлены степени L с неопределенными коэффициентами.
++ Для примера решить уравнение y’’+y’-2y=cos(x)-3sin(x)
47 Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости ряда.
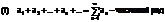
a1,a2 - члены ряда, an=f(n) - общий член ряда, Sn – n-ная частичная сумма Sn=a1+a2+…+an;
Если отбросить первые n членов ряда, то оставшийся ряд называется n-ным остатком и обозначается rn.
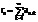
Определение. Числовой ряд наз. сходящимся если существует конечный предел n-ной частичной суммы, где S – сумма ряда
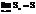
Если при этом предел =∞ или не существует то ряд (1) расходится
Необходимое условие сходимости ряда: Если ряд (1) сходится, то предел
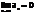
Доказательство:
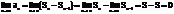
++Стоит заметить, что если условие выполняется ряд может как сходиться, так и расходиться, если же оно не выполняется – то ряд расходится
Признаки сравнения.
Рассмотрим 2 ряда:
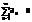
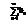 , причём 0≤an≤bn
, причём 0≤an≤bn
1 признак: Тогда, зная, что ряд b сходится, можно утверждать, что ряд а тоже сходится; если ряд а расходится то и ряд b тоже расходится. И никак не наоборот!
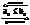
2 признак:Если существует  то ряды a и b сходятся или расходятся одновременно.
то ряды a и b сходятся или расходятся одновременно.
Признаки Даламбера и Коши. Интегральный признак Коши.
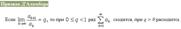
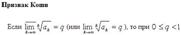



50. Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда .Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
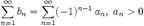 |
Признак Лейбница
Признак Лейбница — признак сходимости знакочередующегося ряда,Формулировка теоремы:
Пусть для ряда 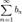 выполняются следующие условия: 1. знакочередование (например: выполняются следующие условия: 1. знакочередование (например: 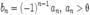 ) 2. an + 1 < an (монотонное убывание {an}) 3. ) 2. an + 1 < an (монотонное убывание {an}) 3. 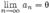 . Тогда этот ряд сходится. . Тогда этот ряд сходится. |
Замечание: Если, выполнены все условия, и ряд из модулей сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно.Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
Пример
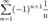 . Ряд из модулей иммет вид
. Ряд из модулей иммет вид 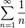 - это гармонический ряд, который расходится.
- это гармонический ряд, который расходится.
Теперь воспользуемся признаком Лейбница:
1. знакочередование выполнено 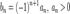
2. 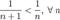
3. 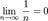 .
.
Следовательно, т.к. все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.
