Модуль 4: Квадратичные формы

Занятие 14. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.

Ауд.: ОЛ-3 гл.4: № 4.213; 4.214; 4.215.

Дома: ОЛ-3 гл.4: № 4.216.

Занятие 15.Приведение уравнения линии второго порядка и поверхности второго порядка к каноническому виду.

Ауд.: ОЛ-3 гл.4: № 4.226; 4.228; 4.235; 4.237.

Дома: ОЛ-3 гл.4: № 4.227; 4.229; 4.233; 4.239.

Занятие 16. Контрольная работа «Квадратичные формы».

Занятие 17.Приведение квадратичной формы методом Лагранжа к нормальному виду. Знакоопределенность квадратичной формы.

Ауд.: ОЛ-3 гл.4: № 4.210; 4.211; 4.218; 4.221; 4.223.

Дома: ОЛ-3 гл.4: № 4.212; 4.219; 4.220; 4.224.

Контрольные мероприятия

Модуль 1: Матрицы и системы линейных алгебраических уравнений (5 неделя, максимум 16 баллов, минимум 8 баллов).

Рубежный контроль по модулю 1 (5 неделя).

Модуль 2: Линейные и евклидовы пространства (9 неделя, максимум 20 баллов, минимум 10 баллов).

Домашнее задание №1 «Линейные и евклидовы пространства» (выдача 6 неделя, прием 9 неделя).

Рубежный контроль по модулю 2 (9 неделя).

Модуль 3: Линейные операторы (13 неделя, максимум 26 баллов, минимум 14 баллов).

Рубежный контроль по модулю 2 (13 неделя).

Модуль 4: Квадратичные формы (17 неделя, максимум 28 баллов, минимум 14 баллов)

Домашнее задание №2 «Приложения квадратичных форм» (выдача 13 неделя, прием 17 неделя).

Рубежный контроль по модулю 2 (17 неделя).

Типовые задания

Домашнее задание №1. «Линейные и евклидовы пространства»

Модуль 2, литература МП-1, МП-2.

Задача 1(2 балла). В линейном пространстве 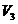свободных векторов выбран правый орто­нор­мированный базис 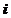, , 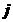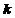. Этот базис поворачивается вокруг заданного вектора 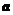(это один из базисных векторов) на заданный угол 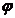в указанном направлении (положительном или отрицательном), а затем вокруг вектора 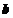(один из базисных векторов в новом положении) на заданный угол 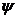в указанном направлении. В результате получается новый базис 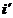, , 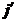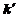. Найти матрицу перехода из старого базиса в новый.

Вариант: , , , .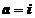

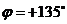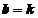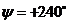Задача 2 (4 балла). В евклидовом пространстве 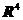задан базис 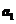, , 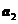, 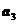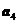(координаты этих векторов определены в стандартном базисе) и два вектора 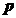и (и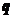х координаты определены в заданном базисе ).

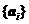1. Применяя процесс ортогонализации, построить по базису 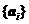новый ортонор­ми­рованный базис .

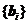2. Найти матрицу перехода от нового базиса 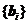к старому базису .

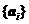3. Найти координаты векторов 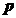и 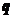в базисе .

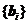4. Вычислить скалярное произведение .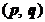

5. Вычислить угол между векторам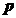и и .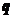

Вариант:

, , , , ,

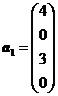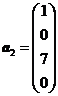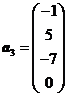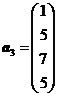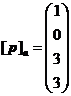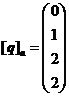
Домашнее задание №2 «Приложения квадратичных форм»

Модуль 4, литература МП-1, МП-2, МП-3.

Уравнение а) линии второго порядка на плоскости в системе координат 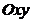и уравнения б) поверхности второго порядка в пространстве в системе координат 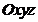привести к каноническому виду, указав:

1) одно из преобразований перехода от заданной системы координат к канонической системе координат (собственные числа ортогонального преобразования расположить в порядке возрастания) ;

2) канонический вид уравнения линии и поверхности, значения всех параметров, характеризующих форму линии и поверхности ;

3) на плоскости построить исходную систему координат 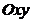, каноническую систему координат 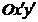, эскиз линии; для центральной линии найти координаты центра, вершин, фокусов, уравнения асимптот (для гиперболы), а для параболы — координаты вершины, фокуса, уравнение директрисы;

4) поверхность построить в канонической системе координат.

Вариант:

а) 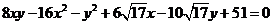; — 4 балла

б) 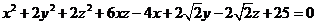.— 6 баллов