Модуль 2. Евклидовы пространства. Билинейные и квадратичные функции

Занятие 6. Евклидовы пространства. Процесс ортогонализации.

Ауд.: ОЛ-2 №№ 4.63(а), 67, 69, (71), 73, (75); ОЛ-3 № 4.1.31; ОЛ-1 № 3.5.

Дома: ОЛ-2 №№ 4.63(б), 64(б), 70, 74.

Занятие 7. Ортогональное дополнение.

Ауд.: ОЛ-2 №№ 4.79; разработка кафедры.

Дома: разработка кафедры

Занятия 8–9. Билинейные функции. Квадратичные формы. Критерий Сильвестра. Метод Лагранжа. Полуторалинейные функции.

Ауд.: ОЛ-2 №№ 4.204, 218, 220, 221, 210, 212; разработка кафедры.

Дома: ОЛ-2 №№ 4.222, 223, 224,211, 212; разработка кафедры.

Модуль 3. Линейные операторы

Занятие 10. Линейные операторы и их матрицы. Преобразование матрицы линейного оператора при переходе к новому базису.

Ауд.: ОЛ-2 №№ 4.83, 85, 87, 89, 91, 93, 97, 113, 106(а).

Дома: ОЛ-2 №№ 4. 84, 86, 90, 95, 97, 106(б), 108, 112; разработка кафедры.

Занятие 11. Собственные значения и собственные векторы. Приведение матрицы линейного оператора к диагональному виду.

Ауд.: ОЛ-2 №№ 4.135, (137, 139, 141, 143), 4.176, 179, 180(б); ОЛ-3 №№ 3.2.16(б).

Дома: ОЛ-2 №№ 4.136, 139, (134, 138, 140, 142), 148, 172, 175, 180(а).

Занятие 12. Инвариантные подпространства. След. Подобие матриц.

Ауд.: ОЛ-3 №№ 3.2.27, 3.2.29; разработка кафедры.

Дома: ОЛ-3 №№ 3.2.28, 3.2.22, 3.2.30; разработка кафедры.

Занятия 13-15. Нахождение жордановой нормальной формы. Нахождение жорданова базиса. Функции от матриц. Аннулирующие и минимальные многочлены.

Ауд.: ОЛ-3 №№ 3.3.1(б,д), 3.3.3, 3.3.19(а), 3.3.7, 3.3.43, 3.3.45, 3.3.21, 3.3.22, 3.3.24(а), 3.3.26.

Дома: ОЛ-3 №№ 3.3.1(б,в), 3.3.3(б)*, № 3.3.1(в) — найти жорданов базис, 3.3.10(а), 3.3.19(б), 3.3.43(а), 3.3.27,3.3.30, 3.3.24.

Занятия 16-17. Самосопряженные и ортогональные операторы. Диагонализация симметрических матриц ортогональным преобразованием.Приведение матрицы ортогонального оператора к каноническому виду. Проекторы.

Ауд.: ОЛ-2 №№ 4.151, 168(а, б)+171, 170, 191, 183; ОЛ-3 №№ 4.4.5(а, б);

Дома: ОЛ-2 №№ 4.152, 168(в)+171, 184, 186; ОЛ-3 №№ 4.4.5(в), 4.3.3; разработка кафедры.

Модуль 4. Аффинные и проективные пространства. Тензоры

Занятия 18-19. Аффинные пространства. Способы задания плоскостей. Взаимное расположение плоскостей. Евклидовы пространства.

Ауд.: ОЛ-3 №№ № 6.1.10(а), 6.1.16(б), 6.1.20(а), 6.3.6(а); ДЛ-4 №№ 1877, 1887, 1337, 1339 (формулировка), 1340, 1374;

Дома: ОЛ-3 №№ 6.1.10(б), 6.1.16(а, в), 6.3.7(а); ДЛ-4 №№ 1338, 1339(доказать), 1341, 1885.

Занятие 20. Аффинные преобразования.

Ауд.: ОЛ-3 №№ 6.1.30, 6.1.31(а), 6.1.33(а), 6.1.28*; ДЛ-3 №№ 1157, 1176.

Дома: ОЛ-3 №№ 6.1.31(б), 6.1.33(б); ДЛ-3 №№ 1156, 1160, 1182.

Занятие 21. Ортогональные преобразования квадратичных форм. Приведение кривых и поверхностей 2-го порядка к каноническому виду.

Ауд.: ОЛ-2 №№ 4.214, 216, 226, 228, 231, (235, 237, 234).

Дома: ОЛ-2 №№ 4.213, 215, 227, 229, 230, (233, 236).

Занятия 22-23. Проективное пространство. Проективные преобразования.

Ауд.: ОЛ-3 №№ 6.5.1(а), 6.5.3(а); ДЛ-3 №№ 1310, 1307, 1397, 1389, 1392.

Дома: ОЛ-3 №№ 6.5.1(б), 6.5.3(б); ДЛ-3 №№ 1310, 1307, 1397, 1389, 1392.

Занятия 24-25. Определение тензоров. Операции над тензорами. Матричная запись тензоров.

Ауд.: разработка кафедры.

Дома: разработка кафедры.

Занятия 26-28. Резерв.

Вопросы для подготовки к экзамену

Модуль 1. Линейные пространства. Линейные функции

1. Линейные (векторные) пространства. Базис. Матрица перехода. Изменение координат вектора при переходе от базиса к базису.

2. Докажите, что два векторных пространства 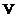и и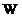зоморфны тогда и только тогда, когда .

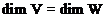3. Линейные подпространства. Сумма и пересечение подпространств. Формула Грассмана.

4. Когда сумма 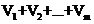подпространств линейного пространства 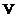является прямой?

5. Линейные функции. Сопряженное пространство. Для любого конечномерного пространства 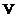имеем .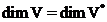

6. Пусть даны два базиса 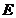и 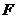линейного пространства 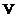, 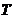— матрица перехода от 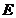к 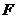. Рассмотрим двойственные базисы 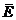и 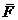. Какова матрица перехода от 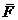к ?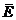

7. Всякое подпространство есть пересечение ядер некоторого множества линейных функций.