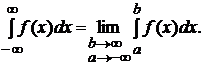Свойства определённого интеграла

1. 
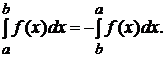
2. Линейность:

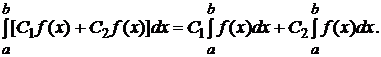
1. Определённый интеграл можно представить в виде суммы интегралов

,

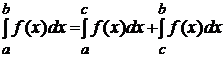если .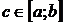

1. Если f(x) ≤ φ(x) при a≤х≤b , то

≤

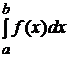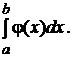
1. Если m – наименьшее, а M – наибольшее значения функции f(x) на отрезке a≤х≤b, то

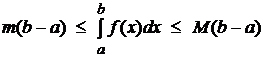
1. Если функция f(x) непрерывна на отрезке a≤х≤b, то на этом отрезке найдётся такая точка x, что

.

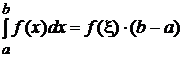Число 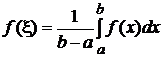называется средневзвешенным значением функции на отрезке [a; b].

Вычисление определенного интеграла.

Формула Ньютона-Лейбница

Если функции f(x) непрерывна на отрезке [a;b] и для нее известен неопределённый интеграл

,

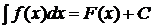где F(x) –первообразная функции f(x), то определенный интеграл может быть вычислен по формуле Ньютона-Лейбница

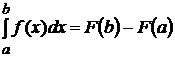, (9.2)

то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

При вычислениях по формуле (9.2) обычно пишут в виде

.

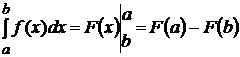Пример:

Вычислить определенные интегралы:

1. .

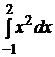Решение: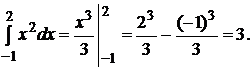

2. .

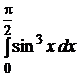Решение: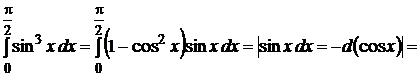

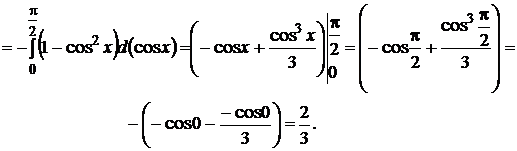
3. .

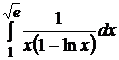Решение: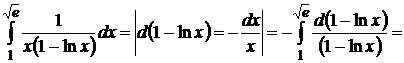

.

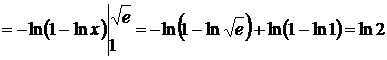Методы вычисления определенных интегралов

Замена переменной в определенном интеграле

При вычислении определенного интеграла 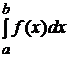часто полезно заменить переменную интегрирования х на новую переменную t при помощи подстановки х = φ(t) или t = ψ(х) (φ(t) и ψ(х) – непрерывные функции, имеющие непрерывные производные на отрезке 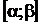). При этом необходимо перейти от старых пределов интегрирования а и b к новым пределам 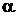и 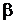, которые определяются из уравнений

, .

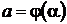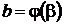Замена переменной осуществляется по формуле

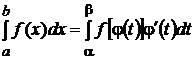. (9.3)

Подчеркнем, что при вычислении определенного интеграла методом замены переменной по формуле (9.3) в отличие от неопределенного интеграла возврат к старой переменной интегрирования не требуется.

Пример:

С помощью подходящих подстановок вычислить интегралы.

1. .

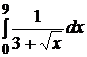Решение:переходим к новой переменной интегрирования, полагая 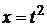(t > 0). При х = 0 получаем t = 0, а при х = 9 – t = 3; поэтому в соответствии с формулой (9.3) получаем

.

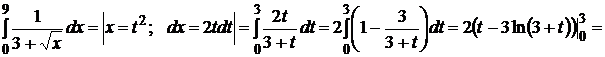
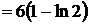2. .

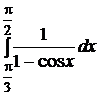Решение:применим универсальную тригонометрическую подстановку 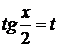. Если 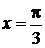, то 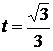, а при 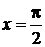– t = 1. Тогда

.

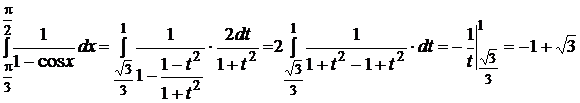3. .

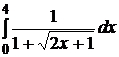Решение:применяя подстановку 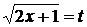(t > 0), получим

.

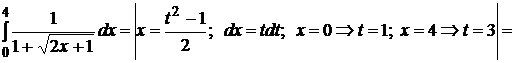
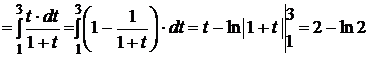Интегрирование по частям в определенном интеграле

Если функции u(x) и v(х) имеют непрерывные производные на отрезке [a; b], то справедлива формула интегрирования по частям для определенного интеграла:

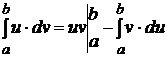, (9.4)

где символ 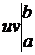обозначает разность .

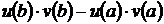Пример:

Применяя формулу (9.4), вычислить интегралы:

1. .

Решение:положим 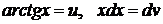, тогда

.

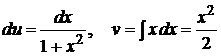Подставляя полученные значения в формулу (9.4) получаем

.

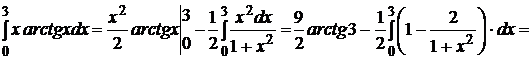
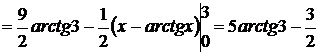2. .

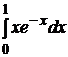Решение:

.

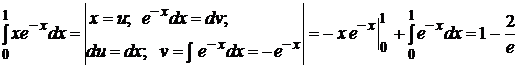В случае, если не удаётся вычислить неопределённый интеграл, то прибегают к приближённым методам вычисления определённых интегралов.

Задания для самостоятельной работы

1. Вычислить определенные интегралы:

1.1. 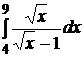; 1.2. 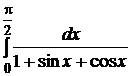; 1.3. ;

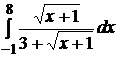1.4. 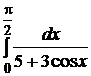; 1.5. .

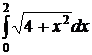2. Вычислить интегралы методом интегрирования по частям:

2.1. 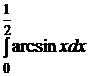; 2.2. 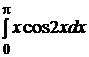; 2.3. 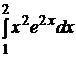; 2.4. .

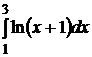Несобственные интегралы

интегралы с бесконечными пределами

Если функция f(x) интегрируема на любом отрезке [a; b], где a < b< ∞, то полагают

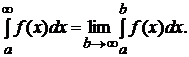(9.5)

Если существует предел в правой части равенства (9.5), то интеграл 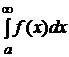называется сходящимся, и расходящимся, если указанный предел не существует.

Аналогично, если функция f(x) интегрируема на любом отрезке [a; b], где – ∞ < a < b, то полагают

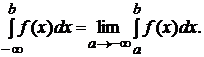
И, если функция f(x) интегрируема на любом отрезке [a; b] числовой оси то,