Правило Лопиталя для раскрытия неопределенностей

Отношение двух бесконечно малых при х→а функций 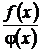можно заменить в пределе на отношение их производных 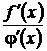, если эти функции дифференцируемы в заданной точке и существует предел отношения их производных. Это правило справедливо и для бесконечно больших функций.

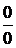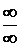При раскрытии неопределённостей вида и можно применить равенство:

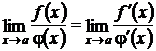. (7.13)

Доказательство этого утверждения следует из теоремы 5 (Коши).

Вычисление предела по формуле (7.13) называется правилом Лопиталя.

Если частное 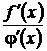в точке х = а также есть неопределённость вида 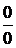или 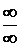, то следует перейти к отношению вторых производных и т.д.

Неопределённости вида 0∙∞ и ∞ – ∞ следует алгебраически преобразовать данную функцию так, чтобы получилась неопределённость 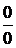или 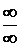и далее воспользоваться правилом Лопиталя.

Неопределённости вида 0⁰ или ∞⁰ или 1^∞ раскрываются после логарифмирования функции и нахождения предела её логарифма.

Пример:

Вычислить данные пределы по правилу Лопиталя:

1.

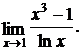
Решение:подстановка предельного значения х = 1 приводит к неопределенности вида 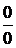. Применяя правило Лопиталя, получим

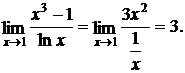
2.

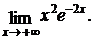
Решение: преобразуем функцию:

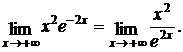Подстановка предельного значения х = ∞ приводит к неопределенности вида 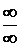. Применяя правило Лопиталя дважды, получим

.

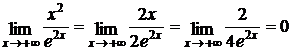3.

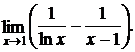
Решение: имеем неопределенность ∞ – ∞. Преобразуем функцию:

.

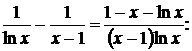
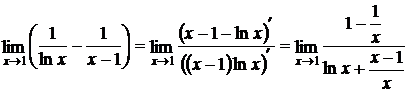4.

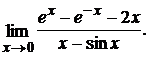
Решение: имеем неопределенность 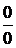. Применяя правило Лопиталя, получим

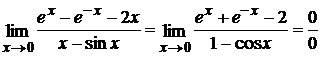– опять получилась неопределенность. Применим правило Лопиталя еще раз.

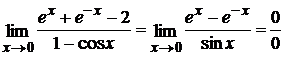– применяем правило Лопиталя еще раз.

.

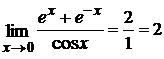Исследование функций

Возрастание и убывание функций. Экстремум функций

Определение. Функция f(х) называется возрастающей в точке х₀, если при любом достаточно малом h > 0 выполняется условие

f(х₀ – h) < f(х₀) < f(х₀ + h).

признаком возрастания функции в точке х₀ является условие f′(х₀) > 0.

Определение. Функция f(х) называется убывающей в точке х₀, если при любом достаточно малом h > 0 выполняется условие f(х₀ – h) > f(х₀) > f(х₀ + h).

признаком убывания функции в точке х₀ является условие f′(х₀) < 0.

Определение. Функция f(х) называется возрастающей в интервале (а;b), если для любых двух точек х₁ и х₂ из этого интервала большему значению аргумента соответствует большее значение функции, т.е. для х₂ > х₁ всегда

f(х₂) > f(х₁).

Определение. Функция f(х) называется убывающей в интервале (а;b), если для любых двух точек х₁ и х₂ из этого интервала большему значению аргумента соответствует меньшее значение функции, т.е. для х₂ > х₁ всегда

f(х₂) < f(х₁).

Определение. Точка х₀ называется точкой локального минимума функции, если при любом достаточно малом h > 0, функция убывает в интервале (х₀–h;х₀), и возрастает в интервале (х₀;х₀+h). Значение f(х₀) называется минимумом функции.

Определение. Точка х₀ называется точкой локального максимума функции, если при произвольном достаточно малом h > 0, функция возрастает в интервале (х₀–h; х₀), и убывает в интервале (х₀; х₀+h). Значение f(х₀) является максимумом функции.

Экстремум функции означает наличие минимума или максимума функции в точке х₀. Точка х₀ есть точка экстремума функции.

Условия существования экстремума функции

Необходимое условие существования экстремума:

Если функция f(х) имеет в точке х₀ экстремум, то производная f '(х) обращается в ноль в точке х = х₀, f '(х₀) = 0 (теорема 2 Ферма), или не существует.

Первый достаточный признак существования экстремума:

Если при произвольном достаточно малом h > 0, выполняются неравенства f '(х₀ – h) > 0 и f '(х₀ + h) < 0, то функция f(х) в точке х₀ имеет максимум. Если же при этих условиях выполняются неравенства f '(х₀ – h) < 0 и f '(х₀ + h) > 0, то функция f(х) в точке х₀ имеет минимум. Говорят, что производная в точке максимума с слева и справа меняет знак с плюса на минус, а в точке минимума – с минуса на плюс.

Второй достаточный признак существования экстремума:

Если f '(х₀) = 0, а f ''(х₀) ≠ 0, то функция f(х) имеет экстремум в точке х₀. При f ''(х₀) < 0 – максимум; при f ''(х₀) > 0 – минимум.

Если f ''(х₀) = 0 (при f '(х₀) = 0), то вопрос о наличии в точке х₀ экстремума или перегиба (переход графика с вогнутости на выпуклость или наоборот) решается взятием следующей по порядку производной, до тех пор, пока не появится производная отличная от нуля f⁽ⁿ⁾(х₀) ≠ 0. При n чётном в точке х₀ будет экстремум, а если n нечётное, то перегиб.