Приведение уравнений кривых к каноническому виду
В новых координатах общее уравнение (3.10) запишем в виде
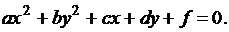 (3.13)
(3.13)
1. Если a = b = 0, то 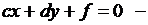 это уравнение прямой линии.
это уравнение прямой линии.
2. Если a или b равно 0, получим уравнение параболы
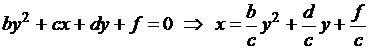 или
или
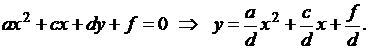
При 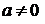 и
и 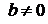 можно уравнение (3.13) разделить на a и записать его в виде
можно уравнение (3.13) разделить на a и записать его в виде
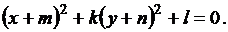 (3.14)
(3.14)
3. Если 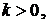 а
а 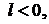 уравнение (3.14) является уравнением эллипса (
уравнение (3.14) является уравнением эллипса ( 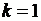 – окружность).
– окружность).
4. Если 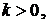 а
а 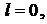 уравнение (3.14) определяет две прямые линии.
уравнение (3.14) определяет две прямые линии.
5. Если 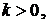 а
а 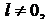 уравнение (3.14) определяет гиперболу.
уравнение (3.14) определяет гиперболу.
Эллипс и окружность
Уравнение 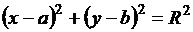 определяет окружность радиуса R с центром С(а;b). Канонический вид уравнения окружности имеет вид:
определяет окружность радиуса R с центром С(а;b). Канонический вид уравнения окружности имеет вид:
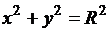 (3.15)
(3.15)
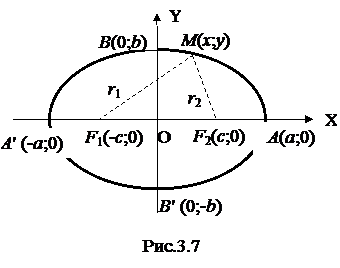
Эллипсомназывается геометрическое место точек, для которых сумма расстояний 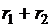 до двух фиксированных точек плоскости, называемых фокусами F1 и F2, есть постоянная величина, равная 2а. (рис.3.7).
до двух фиксированных точек плоскости, называемых фокусами F1 и F2, есть постоянная величина, равная 2а. (рис.3.7).
По определению эллипса

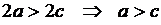 .
.
 Если фокусы эллипса расположить по оси Ох симметрично начала координат, то уравнение эллипса будет иметь канонический вид
Если фокусы эллипса расположить по оси Ох симметрично начала координат, то уравнение эллипса будет иметь канонический вид
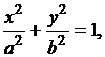 (3.16)
(3.16)
где: 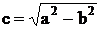 . Очевидно, что
. Очевидно, что 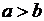 .
.
Оси координат являются осями симметрии эллипса, или просто – осями эллипса. Начало координат – центр симметрии, или просто центр. Точки пересечения эллипса с осями координат А, A′, В, В′ называются его вершинами. Отрезок ОА = а называют большой полуосью эллипса, а ОВ = b – малой полуосью.
Если фокусы эллипса расположены на оси Оу симметрично относительно начала координат, то в этом случае 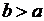 и b будет большой полуосью эллипса. Если
и b будет большой полуосью эллипса. Если 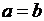 , то уравнение (3.16) переходит в уравнение окружности. Окружность (3.15) является частным случаем эллипса.
, то уравнение (3.16) переходит в уравнение окружности. Окружность (3.15) является частным случаем эллипса.
Отношение фокусного расстояния к большой полуоси, определяет форму эллипса и называется эксцентриситетом
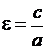 .
.
Очевидно, что эксцентриситет эллипса 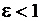 . Чем меньше значение ε, тем ближе форма эллипса к окружности, для которой
. Чем меньше значение ε, тем ближе форма эллипса к окружности, для которой 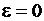 .
.
Эллипсы образуются при проектировании окружности на плоскость образующую угол 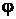 с плоскостью окружности. У проекции
с плоскостью окружности. У проекции 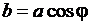 . При сечении цилиндра плоскостью под углом
. При сечении цилиндра плоскостью под углом 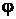 к оси цилиндра образуются эллипсы, у которых
к оси цилиндра образуются эллипсы, у которых 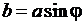 .
.
Гипербола
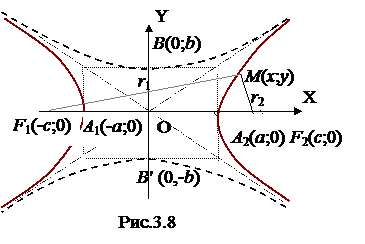
Гиперболой называется геометрическое место точек плоскости, для которых разность расстояний до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная 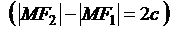 . Если фокусы гиперболы расположить по оси Ох симметрично начала координат, то уравнение гиперболы будет иметь канонический вид:
. Если фокусы гиперболы расположить по оси Ох симметрично начала координат, то уравнение гиперболы будет иметь канонический вид:
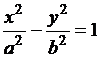 , (3.17)
, (3.17)
 где
где 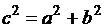 . Построение гиперболы удобно начинать с построения прямоугольника со сторонами а и b (рис.3.8), диагонали которого
. Построение гиперболы удобно начинать с построения прямоугольника со сторонами а и b (рис.3.8), диагонали которого 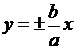 проходят через начало координат и являются асимптотами гиперболы. Отрезок ОА = а называют действительной полуосью гиперболы, а ОВ = b – мнимой полуосью гиперболы.
проходят через начало координат и являются асимптотами гиперболы. Отрезок ОА = а называют действительной полуосью гиперболы, а ОВ = b – мнимой полуосью гиперболы.
Отношение
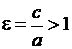
называется эксцентриситетом гиперболы. Гипербола состоит из двух ветвей. Точки A1 (-a;0) и A2 (a;0) называются вершинами гиперболы.
На рис.3.8 пунктиром изображена гипербола 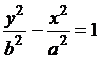 . У этой гиперболы а – мнимая полуось, а b – действительная полуось гиперболы.
. У этой гиперболы а – мнимая полуось, а b – действительная полуось гиперболы.
Если а = b, то х2 – у2 = а2 – уравнение равнобочной гиперболы. Её асимптоты образуют прямой угол. Если эти асимптоты принять за оси координат, то уравнение равнобочной гиперболы преобразуется в уравнение обратной, пропорциональной зависимости между у и х, 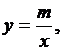 где
где 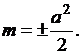
Парабола
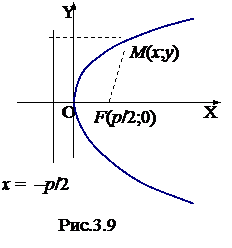 Параболой называется множество точек плоскости, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Принято директрису
Параболой называется множество точек плоскости, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Принято директрису 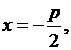 проводить параллельно оси Y, а фокус F(p/2; 0) располагать на оси ОX по другую сторону от начала координат.
проводить параллельно оси Y, а фокус F(p/2; 0) располагать на оси ОX по другую сторону от начала координат.
Уравнение параболы имеет вид
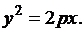 (3.18)
(3.18)
Ось абсцисс является осью симметрии параболы (3.18). При р > 0 (рис. 3.9) ветви параболы обращены в положительную сторону оси ОX. При р < 0 – в отрицательную сторону.
Парабола 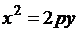 симметрична относительно оси ординат. Её вершина точка О располагается в начале координат.
симметрична относительно оси ординат. Её вершина точка О располагается в начале координат.
При параллельном переносе осей координатуравнение параболы принимает канонический вид 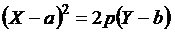 . После раскрытия скобок и определения Y получим традиционную форму параболы
. После раскрытия скобок и определения Y получим традиционную форму параболы
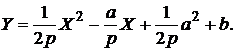
Пример:
Установить тип кривых и привести их к каноническому виду:
а) 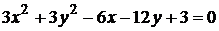 ;
;
б) 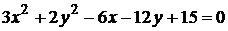 (сделать чертеж);
(сделать чертеж);
в) 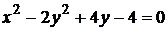 ;
;
г) 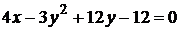 .
.
Решение:а) разделим уравнение на 3 и приведем его к виду (3.14):
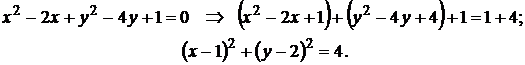
Полученное равенство определяет окружность с центром в точке С(1;2) радиуса R = 2.
С помощью подстановки 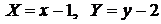 приведем полученное уравнение окружности к каноническому виду
приведем полученное уравнение окружности к каноническому виду
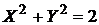 – окружность.
– окружность.
б) 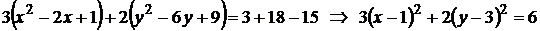 .
.
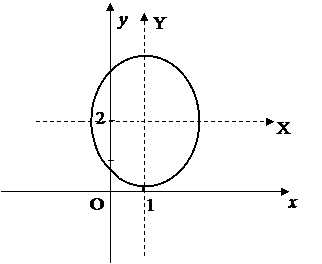 Сделав подстановку
Сделав подстановку 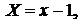
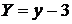 , получим каноническое уравнение эллипса
, получим каноническое уравнение эллипса
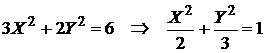 .
.
полученая кривая эллипс представлена на рисунке.
Ответ:в) 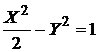 – гипербола; г)
– гипербола; г) 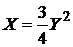 – парабола с осью симметрии OY.
– парабола с осью симметрии OY.
Плоскость в пространстве
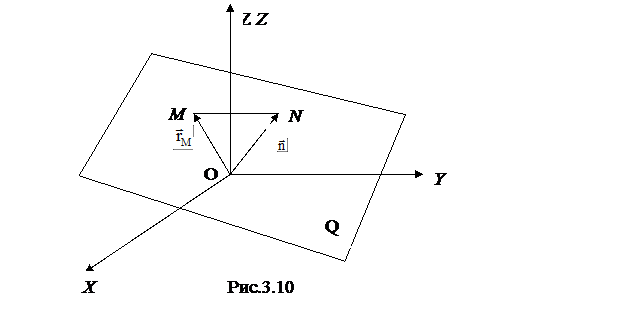
Из начала координат можно опустить на плоскость перпендикуляр и притом только один. Из этого геометрического заключения вытекает правило: направление перпендикуляра, опущенного из начала координат, и его длина определяют данную плоскость единственным способом.
На рис.3.10 изображена часть плоскости Q, на которую опущен перпендикуляр ON. На плоскости выбрана произвольная точка M(x;y;z). Поскольку МN перпендикулярна ON, то проекция радиус–вектора 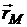 на вектор
на вектор 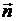 равна
равна 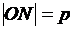 . То есть, для любой точки плоскости Q
. То есть, для любой точки плоскости Q
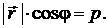 (3.19)
(3.19)
Выберем на векторе 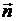 единичный вектор
единичный вектор 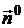 (орт вектора
(орт вектора 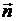 ), и умножим обе части уравнения (1.19) на
), и умножим обе части уравнения (1.19) на 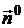 .
.
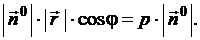
Левая часть полученного уравнения есть скалярное произведение векторов 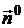 и
и 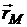 , а правая часть равна p – длине перпендикуляра ON, поскольку
, а правая часть равна p – длине перпендикуляра ON, поскольку 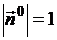 . Тогда
. Тогда
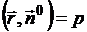
есть уравнение плоскости в векторной форме. Перейдя к координатам, получим нормальное уравнение плоскости
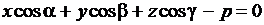 , (3.20)
, (3.20)
 где
где 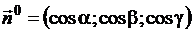 ,
, 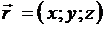 , р – расстояние от начала координат до плоскости.
, р – расстояние от начала координат до плоскости.
Общее уравнение плоскости
Уравнение (3.20) показывает, что любое уравнение вида
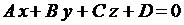 (3.21) можно рассматривать как уравнение плоскости (общее уравнение), если
(3.21) можно рассматривать как уравнение плоскости (общее уравнение), если 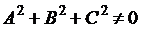 . Здесь А, В и С являются как координатами вектора
. Здесь А, В и С являются как координатами вектора 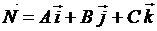 , перпендикулярного плоскости. В тоже время
, перпендикулярного плоскости. В тоже время 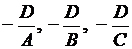 – точки пересечения плоскости с координатными осями.
– точки пересечения плоскости с координатными осями.
Для приведения общего уравнения плоскости к нормальному виду надо уравнение (3.22) умножить на нормирующий множитель
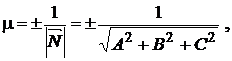 (3.22)
(3.22)
где знак перед радикалом противоположен знаку перед D в уравнении (3.22).
Вектор 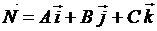 называется нормальным вектором плоскости.
называется нормальным вектором плоскости.
Частные случаи общего уравнения плоскости определим на основании геометрических суждений относительно оси Ох. Поскольку координатные оси равноправны, то для других осей будут аналогичные формулы.
Плоскость 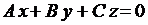 (p = 0 в уравнении 3.21) проходит через начало координат.
(p = 0 в уравнении 3.21) проходит через начало координат.
Плоскость 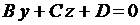 – параллельна оси Ох.
– параллельна оси Ох.
Плоскость 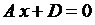 – перпендикулярна оси Ох.
– перпендикулярна оси Ох.
Плоскость 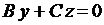 проходит через начало координат и ось Ох.
проходит через начало координат и ось Ох.
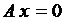 – совпадает с плоскостью уОz. То есть
– совпадает с плоскостью уОz. То есть 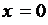 – уравнение координатной плоскости уОz.
– уравнение координатной плоскости уОz.
