Линейное (векторное) пространство
Как известно, линейные операции (сложение, вычитание, умножение на число) определены по-своему для каждого множества (числа, многочлены, направленные отрезки, матрицы). Сами операции различны, но их свойства одинаковы.
Эта общность свойств позволяет обобщить понятие линейных операций для любых множеств вне зависимости от того, что это за множества (числа, матрицы и т.д.).
Для того, чтобы дать определение линейного (векторного) пространства рассмотрим некоторое множество L действительных элементов, для которых определены операции сложения и умножения на число.
Эти операции обладают свойствами:
1) Коммутативность  +
+  =
=  +
+ 
2) Ассоциативность (  +
+  ) +
) + 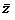 =
=  + (
+ (  +
+ 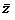 )
)
3)Существует такой нулевой вектор 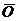 , что
, что 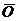 +
+  =
=  для "
для "  Î L
Î L
4) Для "  Î L существует вектор
Î L существует вектор  = -
= -  , такой, что
, такой, что  +
+  =
= 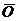
5)1×  =
= 
6) a(b  ) = (ab)
) = (ab) 
7) Распределительный закон (a + b)  = a
= a  + b
+ b 
8) a(  +
+  ) = a
) = a  + a
+ a 
Определение: Множество L, элементы которого обладают перечисленными выше свойствами, называется линейным (векторным) пространством, а его элементы называются векторами.
Линейные преобразования
Определение: Будем считать, что в линейном пространстве L задано некоторое линейное преобразование А, если любому элементу  Î L по некоторому правилу ставится в соответствие элемент А
Î L по некоторому правилу ставится в соответствие элемент А  Î L.
Î L.
Определение: Преобразование А называется линейным, если для любых векторов  Î L и
Î L и  Î L и любого a верно:
Î L и любого a верно:
A(  +
+  ) = A
) = A  +A
+A 
A(a  ) = aA
) = aA 
Пример. Является ли А линейным преобразованием. А  =
=  +
+ 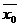 ;
; 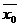 ¹ 0.
¹ 0.
Запишем преобразование А для какого- либо элемента  . А
. А  =
=  +
+ 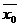
Проверим, выполняется ли правило операции сложения для этого преобразования А(  +
+  ) =
) =  +
+  +
+ 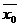 ; A(
; A(  ) + A(
) + A(  ) =
) =  +
+ 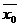 +
+  +
+ 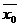 , что верно только при
, что верно только при 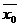 = 0, т.е. данное преобразование А нелинейное.
= 0, т.е. данное преобразование А нелинейное.
Матрицы линейных преобразований
Пусть в n- мерном линейном пространстве с базисом 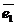 ,
, 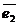 ,…,
,…, 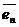 задано линейное преобразование А. Тогда векторы А
задано линейное преобразование А. Тогда векторы А 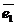 ,А
,А 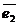 ,…,А
,…,А 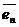 - также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:
- также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:
A 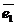 = a11
= a11 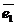 + a21
+ a21 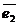 +…+ an1
+…+ an1 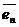
A 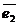 = a12
= a12 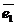 + a22
+ a22 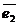 +…+ an2
+…+ an2 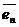
……………………………….
A 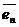 = an1
= an1 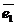 + an2
+ an2 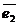 +…+ ann
+…+ ann 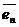
Тогда матрица А = 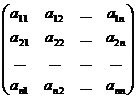 называется матрицей линейного преобразования А.
называется матрицей линейного преобразования А.
Если в пространстве L взять вектор  = x1
= x1 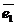 + x2
+ x2 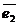 +…+ xn
+…+ xn 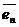 , то A
, то A  Î L.
Î L.
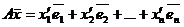 , где
, где
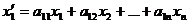
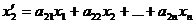
……………………………..
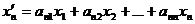
Эти равенства можно назвать линейным преобразованием в базисе 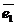 ,
, 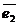 ,…,
,…, 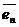 .
.
В матричном виде:
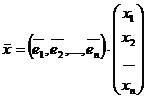 , А×
, А× 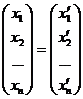 ,
, 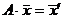
Пример. Найти матрицу линейного преобразования, заданного в виде:
x¢ = x + y
y¢ = y + z
z¢ = z + x
x¢ = 1×x + 1×y + 0×z
y¢ = 0×x + 1×y + 1×z
z¢ = 1×x + 0×y + 1×z
A = 
На практике действия над линейными преобразованиями сводятся к действиям над их матрицами.
Определение: Если вектор  переводится в вектор
переводится в вектор  линейным преобразованием с матрицей А, а вектор
линейным преобразованием с матрицей А, а вектор  в вектор
в вектор 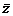 линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор
линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор  в вектор
в вектор 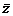 (оно называется произведением составляющих преобразований).
(оно называется произведением составляющих преобразований).
С = В×А
Пример. Задано линейное преобразование А, переводящее вектор  в вектор
в вектор  и линейное преобразование В, переводящее вектор
и линейное преобразование В, переводящее вектор  в вектор
в вектор 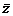 . Найти матрицу линейного преобразования, переводящего вектор
. Найти матрицу линейного преобразования, переводящего вектор  в вектор
в вектор 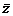 .
.
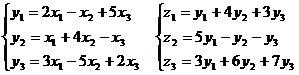
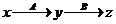
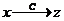
С = В×А
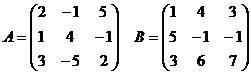
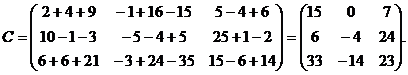
Т.е. 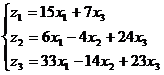
Примечание: Если ïАï= 0, то преобразование вырожденное, т.е., например, плоскость преобразуется не в целую плоскость, а в прямую.
