Понятие об n-мерном векторе. Векторное пространство.

Умножение матриц . Транспонирование матриц и их свойства. Примеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом: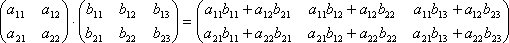

В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно, 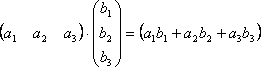Транспонирование. если 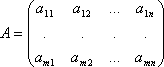, то . 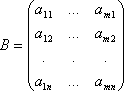Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.Связь между матрицей A и её транспонированной можно записать в виде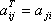

4.Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: 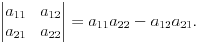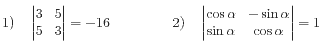Определителем третьего порядка называется следующее выражение: 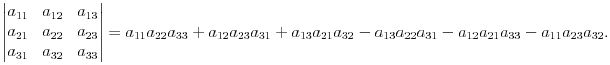Правило треугольников: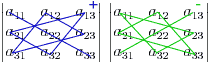

Пример: А= 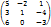det A= 5×1×(-3)+(-2)×(-4)×6+3×0×1- 6×1×1-3×(-2)×(-3)-0×(-4)×5=-15+48-6-18=9

Определитель квадратной матрицы n-ного порядка равен алгебраической сумме парных произведений элементов i-той строки матрицы А на их алгебраические дополнения или j-го столбца на их алгебраические дополнения.

Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения

5.Свойства определителей.

1. Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами).

2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

3. От перестановки двух строк определитель меняет свой знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки умножить на некое число, то сам определитель умножится на это число.

6. Определитель, содержащий две пропорциональные строки или 2 пропорциональных столбца, равен нулю.

7. Если все элементы i-й строки определителя n-го порядка представлен в виде суммы двух слагаемых: aij=bj+cj, j = 1, ..., n, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, - такие же, как и в заданом определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.

8. Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен нулю..

9. Определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк.

10. Определитель двух квадратных матриц одного и того же порядка равен произведению определителей этих матриц.

11. Определитель верхней треугольной матрицы равен произведению диагональных элементов. A11 A22 Ann

Теорема (о разложении определителя по строке): определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения. Это означает, что определитель матрицы n×n равен 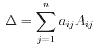(алгебраическое дополнение Aij=(-1)i+jMij. Здесь минор Mij - определитель получаемый из основного определителя вычеркиванием i-й строки и j-го столбца)

Теорема о разложении определителя по строке позволяет свести вычисление определителя матрицы n×n к вычичлению n определителей матриц (n-1)×(n-1). Таким образом, вычисление определителей с порядком выше третьего сводится к разложению на сумму определителей третьего порядка.

6. Обратная матрица.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если det = 0. Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В. Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Матрица, обратная матрице А, обозначается через А^-1, так что В = А^-1. Свойства обратных матриц

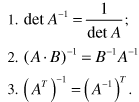
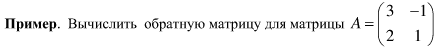
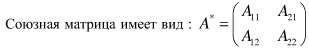
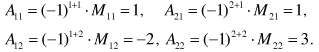
Считаем det=1/5.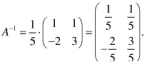

7. Минором некоторого элемента аij , определителя матрицы n - ого порядка называется определитель (n - 1) - ого порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент аij. Обозначается Мij.

Любой минор, отличный от 0, порядок которого равен рангу, называется базисным.

В матрице А выделим k произвольных строк и k столбцов. Составим det. Полученныйdet k-го порядка назыв минором к-го порядка. Ранг А- наивысший порядок ее миноров, отличных от 0. Теорема: Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк. Привести матрицу к виду верхней треуг или трапециевидной. Ранг- число ненулевых строк.

8.Матричный метод

Пусть дана система из 3-х уравнений с тремя неизвестными 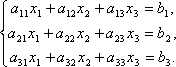. 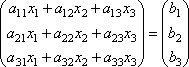Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A: . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

9.Метод Крамера.

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными: 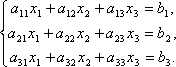Находим det

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём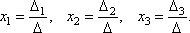

10. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

· перестановка строк или столбцов;

· умножение строки на число, отличное от нуля;

· прибавление к одной строке другие строки.

· Удаление нулевой строки

Любая СЛАУ может быть преобразована к виду системы, у которой расширенная матрица будет иметь ступенчатый вид.

Приведение системы к ступенчатому виду или расширенную матрицу к виду трапециевидной называется прямой ход Гаусса. Обратный ход – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым. Придавая неизвестным (называемым свободными) произвольные значения, получим треугольную систему из которой последовательно найдем все остальные неизвестные (называемые базисными).

Критерии совместимости СЛАУ. Теорема Кронекера-Капелли: СЛУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы. Система ур-ий называется совместной, если она имеет хотя бы одно решение.

Следствия:

1.Если r(A/B)=r(A), СЛАУ совместна, в прот случае нет.

2. r(A/B)=r(A)=n, n- число неизвестных.

3. r(A/B)=r(A)= r r<n, бесконечно много решений.

Общее уравнение плоскости.

Ax+By+Сz-Ax₀-By₀-Сz₀=0

-Ax₀-By₀-Сz₀=D, где D=Ax+By+Сz

Ax+By+Сz+D=0

Частный случай:

Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)

Если A=0, то By+Сz+D=0

Если B=0, то Ax +Сz+D=0

Если C=0, то Ax+By+D=0

Если A=B=0, то Сz+D=0

Если A=C=0, то By+D=0

Если A=D=0, то By+Сz=0

Если B=D=0, то Ay+Сz=0

Линейные ДУ 1-го порядка.

Уравнение вида ,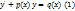

где p(x) и q(x) – заданные функции, назыв. линейным дифференциальным уравнением 1-го порядка. Если в ур-нии 1 правая часть тождественно равна 0, то получим ур-ние вида 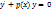(2) (однородное линейное ДУ 1-го порядка)

2—решают как ур-ние с раздел. переменными

1—решают с помощью подстановки:

,

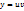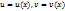
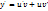
(u’v+uv’)+p(x)uv=q(x)

u’v+u(v’+p(x)v)=q(x)

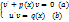
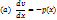
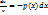
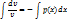
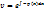
Подставляем во 2-ое уравнение системы (b):

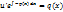
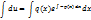
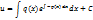
Общее решение уравнения :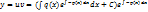

Линейные ДУ 2-го порядка.

Вид:

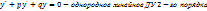
Методика решения:

Уравнение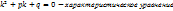

Общее решение зависит от корней характеристического.

a) D<0, 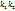, тогда решение имеет вид:

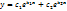
b)D=0, =>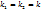

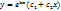
c) D<0, =>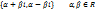

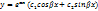
Лин неоднор ДУ 2-го порядка с пост коэфф-ми.

Рассмотрим уравнение y´´+py´+qy=r(x) /где p,q ? R .

которое имеет вид y=yO+yЧ, где

yO-общее решение уравнения y´´+py´+qy =0

yЧ-частное решение уравнения y´´+py´+qy=r(x) , которое зависит от вида правой части,т.е r(x)

Рассмотрим некоторые частные случаи:

1) r(x)=Pn(x) ,где Pn(x) – многочлен степени «n»

В этом случае решение yЧ ищут из уравнения к²+pк+q=0 в виде:

• yЧ=Qn(x) при q≠0

• yЧ=x Qn(x) q=0, p≠0

• yЧ=x² Qn(x) q=p=0

2) r(x)=а 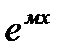где а,м ? R , а,м =соnst

Вид частного решения следущее:

• yЧ=А 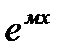если «м» не явл корнем Ур-я к²+pк+q=0

(корни некратные,некомплексные)

• yЧ=Аx 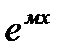если «м» –простой корень ур-я к²+pк+q=0

•yЧ=Аx² 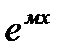если «м»-кратный корень Ур-я к²+pк+q=0

3) r(x)=acosmx+bsinmx где a,b,m=const

• yЧ= Acosmx+Bsinmx при условии что p²+(q-m²)≠0

• yЧ= x(Acosmx+Bsinmx) если p²+(q-m²)=0, p=0,q= m²

Умножение матриц . Транспонирование матриц и их свойства. Примеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом: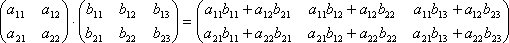

В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно, 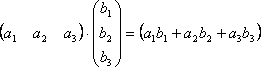Транспонирование. если 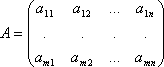, то . 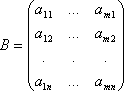Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.Связь между матрицей A и её транспонированной можно записать в виде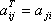

4.Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: 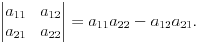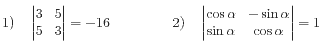Определителем третьего порядка называется следующее выражение: 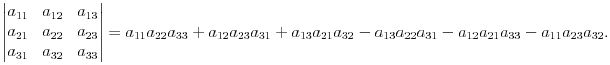Правило треугольников:

Пример: А= 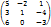det A= 5×1×(-3)+(-2)×(-4)×6+3×0×1- 6×1×1-3×(-2)×(-3)-0×(-4)×5=-15+48-6-18=9

Определитель квадратной матрицы n-ного порядка равен алгебраической сумме парных произведений элементов i-той строки матрицы А на их алгебраические дополнения или j-го столбца на их алгебраические дополнения.

Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения

5.Свойства определителей.

1. Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами).

2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

3. От перестановки двух строк определитель меняет свой знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки умножить на некое число, то сам определитель умножится на это число.

6. Определитель, содержащий две пропорциональные строки или 2 пропорциональных столбца, равен нулю.

7. Если все элементы i-й строки определителя n-го порядка представлен в виде суммы двух слагаемых: aij=bj+cj, j = 1, ..., n, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, - такие же, как и в заданом определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.

8. Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен нулю..

9. Определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк.

10. Определитель двух квадратных матриц одного и того же порядка равен произведению определителей этих матриц.

11. Определитель верхней треугольной матрицы равен произведению диагональных элементов. A11 A22 Ann

Теорема (о разложении определителя по строке): определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения. Это означает, что определитель матрицы n×n равен 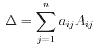(алгебраическое дополнение Aij=(-1)i+jMij. Здесь минор Mij - определитель получаемый из основного определителя вычеркиванием i-й строки и j-го столбца)

Теорема о разложении определителя по строке позволяет свести вычисление определителя матрицы n×n к вычичлению n определителей матриц (n-1)×(n-1). Таким образом, вычисление определителей с порядком выше третьего сводится к разложению на сумму определителей третьего порядка.

6. Обратная матрица.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если det = 0. Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В. Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Матрица, обратная матрице А, обозначается через А^-1, так что В = А^-1. Свойства обратных матриц

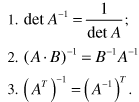
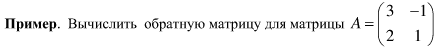
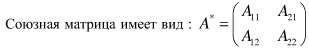
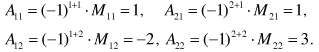
Считаем det=1/5.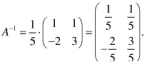

7. Минором некоторого элемента аij , определителя матрицы n - ого порядка называется определитель (n - 1) - ого порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент аij. Обозначается Мij.

Любой минор, отличный от 0, порядок которого равен рангу, называется базисным.

В матрице А выделим k произвольных строк и k столбцов. Составим det. Полученныйdet k-го порядка назыв минором к-го порядка. Ранг А- наивысший порядок ее миноров, отличных от 0. Теорема: Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк. Привести матрицу к виду верхней треуг или трапециевидной. Ранг- число ненулевых строк.

8.Матричный метод

Пусть дана система из 3-х уравнений с тремя неизвестными 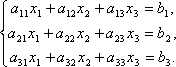. 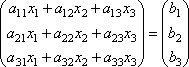Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A: . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

9.Метод Крамера.

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными: 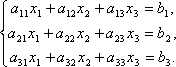Находим det

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём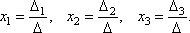

10. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

· перестановка строк или столбцов;

· умножение строки на число, отличное от нуля;

· прибавление к одной строке другие строки.

· Удаление нулевой строки

Любая СЛАУ может быть преобразована к виду системы, у которой расширенная матрица будет иметь ступенчатый вид.

Приведение системы к ступенчатому виду или расширенную матрицу к виду трапециевидной называется прямой ход Гаусса. Обратный ход – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым. Придавая неизвестным (называемым свободными) произвольные значения, получим треугольную систему из которой последовательно найдем все остальные неизвестные (называемые базисными).

Критерии совместимости СЛАУ. Теорема Кронекера-Капелли: СЛУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы. Система ур-ий называется совместной, если она имеет хотя бы одно решение.

Следствия:

1.Если r(A/B)=r(A), СЛАУ совместна, в прот случае нет.

2. r(A/B)=r(A)=n, n- число неизвестных.

3. r(A/B)=r(A)= r r<n, бесконечно много решений.

Понятие об n-мерном векторе. Векторное пространство.

Вектор – направленный отрезок на плоскости или в пространстве, имеющий определённую длину, у которого одна из точек принята за начало, а другая за конец. Длиной вектора (нормой) или модулем называется число, равное длине отрезка, изображающего вектор [ïaï=Öx²+y²(+z²)].Если начало и конец вектора совпадают, то такой вектор называется нулевым и обозначается `0. Для каждого `а, отличного от 0, существует противоположный -`а, который имеет модуль, равный ïаï, коллиниарен с ним, но направлен в другую сторону. Два вектора `а и`в называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Два вектора называются равными, если они: 1)имеют равные модули; 2)коллиниарны; 3)направлены в одну сторону.

n-мерный вектор- упорядоченный набор n чисел, где каждое из n чисел- соответствующие координаты вектора.x=(x₁,x₂,x_i,x_n) Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее всем сво-вам суммы( коммутативное, ассоциативные), называется векторным пространством. Размерность векторного пространства равна количеству векторов в базисе этого пространства. Совокупность n-мерных векторов, рассматриваемая с определёнными в ней операциями сложения векторов и умножения вектора на число, называется n-мерным координатным пространством. Система n—мерных лин. независимых векторов называется базисом Rⁿ (R²-плоскость,R³-пространство), если каждый вектор этого пространства R разлагается по векторам этой системы. Базисом называется совокупность всех лин. независимых векторов системы пространства. Теорема: если диагональная система является частью n-мерных векторов, то она же является базисом этой системы. Теорема: любой вектор системы векторов единственным образов разлагается по векторам её базиса.