Прямые и обратные задачи диагноза.

Назовем прямыми задачами диагноза задачи определения по заданной элементарной проверке 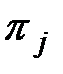той или иной информации о технических состояниях объекта диагноза. При построении алгоритмов диагноза такой информацией может быть, например, определение подмножеств технических состояний объекта, дающих одинаковые результаты элементарной проверки 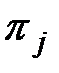. А при реализации алгоритма диагноза интересующей нас информацией может быть определение по известному результату 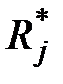элементарной проверки 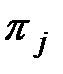подмножества тех технических состояний, в одном из которых фактически находится объект. Указанная информация может представляться не в терминах технических состояний объекта, а в терминах его неисправностей.

Для решения прямых задач диагностирования необходимо предварительно построить математическую модель исправного объекта и произвести необходимое множество допустимых элементарных проверок предполагаемых неисправностей.

В результате решения прямых задач на первом этапе определяется множество тех технических состояний объекта, в одном из которых фактически он находится. Такие задачи решают по результату одной - двух проверок. Далее прогноз уточняют путем использования последующих проверок с применением различных средств и методов контроля. При диагностировании сложных многофункциональных объектов оператору приходится многократно повторять проверки для локализации возникшей неисправности. Часто возникает необходимость в процессе проверок комбинировать различные методы и средства с целью достижения поставленной задачи.

Пусть заданы: математическая модель Ψ исправного объекта диагноза, множество S возможных неисправностей и множество П допустимых элементарных проверок. Модель исправного состояния объекта позволяет ввести в нее любую неисправность 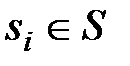и вычислить результаты любой элементарной проверки 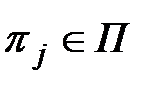по известному значению 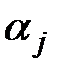ее воздействия.

Вычисление строки таблицы функции неисправностей производится путем многократного решения прямой задачи анализа модели Ψ, состоящего в том, что на модель Ψ подается входное воздействие 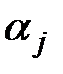элементарной проверки 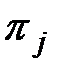и производится вычисление результатов либо 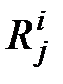, либо 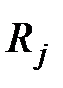. В первом случае в модель предварительно вводится неисправность 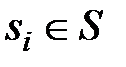(рис.5). В результате будут получены |S|+1 результатов элементарной проверки 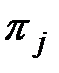для всех i=0,1,2, …, |S|.

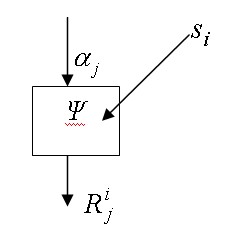
Рис. 5. Представление модели объекта с введением в нее неисправности

Под обратными задачами диагностирования понимается определение некоторой совокупности элементарных проверок, которые позволяют определить заданное техническое состояние объекта, т.е. если в объекте предполагается какая-то неисправность. Решение обратных задач диагностирования позволяет получить все возможные элементарные проверки, обнаруживающие эту неисправность.

Обратные задачи диагностирования заключаются в том, что при известном техническом (неисправном) состоянии изделия необходимо найти такие проверки (методы контроля, программы), которые с высокой степенью точности выявляют это состояние, то есть, возникшую неисправность. Необходимость решения обратных задач диагностирования возникает, как правило, при составлении алгоритмов диагностирования, когда оператору из большого количества методик надо выбрать одну или несколько для практической реализации.

Как и при рассмотрении прямых задач, заданными являются математическая модель исправного объекта, множество возможных неисправностей S и множество П допустимых элементарных проверок. Примем, что модель Ψ позволяет вычислять не только результат 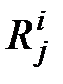, но также для любой неисправности 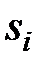вычислять значение 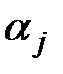воздействия некоторой элементарной проверки 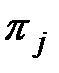по известному ее результату 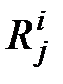, т.е. решать обратную задачу анализа. Построение столбца таблицы функций неисправностей состоит в последовательном вычислении по модели Ψ с введенной в нее неисправностью 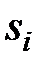результатов 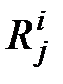каждой элементарной проверки 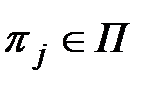. В итоге будут получены |П| результатов 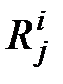элементарных проверок для всех j=1,2, …,|П|. Применение этого алгоритма для каждого i=0,1, …,|S|-1 позволяет заполнить всю П-таблицу функций неисправностей.

Алгоритмы диагноза.

Алгоритм диагноза задает совокупность элементарных проверок, последовательность их реализации и правила обработки результатов реализуемых элементарных проверок.

Результаты любой элементарной проверки могут быть использованы как признаки разбиения множестваЕ технических состояний объекта или подмножеств этого множества на классы. Любой алгоритм диагноза можно представить некоторым ориентированным графом. Ограничимся случаем, когда граф, представляющий алгоритм диагноза является деревом.

Дерево имеет вершины двух типов: вершины, из которых исходит хотя бы одна дуга, и вершины, из которых не отходит ни одной дуги.

Пример дерева дан на рис.6, где вершины первого типа представлены зачерненными кружками, а вершины второго типа – светлыми. В дереве имеется единственная вершина первого типа, в которую не заходит ни одна дуга. Эта вершина называется начальной, или корнем дерева (t₀, E). Вершины, из которых не исходит ни одной дуги, называются конечными, или висячими. Остальные вершины дерева называются внутренними. В каждую вершину дерева, кроме его корня, заходит только одна дуга. В дереве нет контуров.

Рангом вершины дерева называется число дуг пути, начинающегося в начальной вершине и заканчивающегося в рассматриваемой вершине. Минимальным рангом 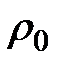дерева является ранг, для которого существует хотя бы одна висящая вершина и не существует ни одной висящей вершины ранга меньше 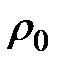. Максимальным рангом 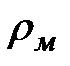дерева является ранг, для которого существует хотя бы одна вершина ранга 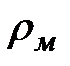и не существует ни одной вершины ранга больше .

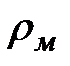Рис. 6. Дерево алгоритма диагноза

Будем внутренние и висящие вершины дерева нумеровать парой чисел в скобках(ρ, σ),где ρ – есть ранг вершины, а σ – ее порядковый номер среди всех вершин одного и того же ранга (например, слева направо). Начальную вершину будем обозначать парой (0,0). Начальной и внутренней вершине сопоставим элементарные проверки множества П. Дугам дерева, исходящей из некоторой его вершины, сопоставим возможные результаты проверки, представляемой этой вершиной. Начальной вершине поставим в соответствие множествоЕвозможных технических состояний объекта, а внутренним и висящим вершинам – подмножества технических состояний, получаемые как классы разбиений по результатам соответствующих элементарных проверок. 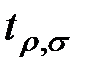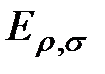Элементарную проверку и подмножество технических состояний, сопоставляемые вершине(ρ, σ)дерева будем обозначать символами и соответственно. Множество элементарных проверок 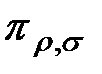обозначим символом П_д. Из правил построения дерева следует, что объединение множества технических состояний есть множествоЕвозможных технических состояний. Каждому пути соответствует последовательность элементарных проверок.

Рассмотрим, как дерево представляет алгоритм диагноза. Начальной вершине соответствует элементарная проверка 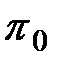множествоЕ всех возможных технических состояний. Элементарная проверка имеет три возможные результата, и тем самым разбивает множествоЕ на три подмножества Е_1,1, Е_1,2, Е_1,3 не различаемых этой проверкой технических состояний. Первые два из этих подмножеств соответствуют внутренним вершинам (1,1) и (1,2) и подлежат дальнейшим разбиениям элементарными проверкам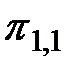и и 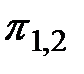. Третье подмножество соответствует висящей вершине, и поэтому разбиение его на подмножества алгоритмом не предусмотрено. Аналогично можно рассмотреть любую другую вершину дерева. Как только в процессе элементарных проверок будет достигнута висящая вершина, алгоритм диагноза прекращается. Фактическое техническое состояние объекта принадлежит подмножеству, соответствующему достигнутой висящей вершине. Каждой конкретной реализации алгоритма диагноза соответствует единственный путь. Например, если фактическое техническое состояние принадлежит подмножеству Е_3,2, то последовательность реализации элементарных проверок будет , , .

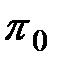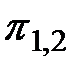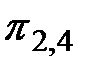Рассмотрим некоторый ненулевой ранг дерева. В общем случае дерево может иметь несколько внутренних вершин. Это значит, что возможны две разные последовательности реализации элементарных проверок. Обе эти проверки могут являться как одной и той же элементарной проверкой 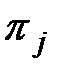множества П, так и разными элементарными проверками последнего. Если для каждого ранга дерева выполняется условие, состоящее том, что всем внутренним вершинам этого ранга сопоставлена одна и та же элементарная проверка из множества П, то алгоритм диагноза называется безусловным. Это соответствует заданию одной фиксированной последовательности реализации элементарных проверок из множества П, не зависящей от фактического технического состояния объекта. Т.е. выбор или назначение очередной элементарной проверки в последовательности их реализации не зависит от результатов предыдущих уже реализованных элементарных проверок. Если же в дереве найдется хотя бы один ранг с несколькими внутренними вершинами, которым сопоставимы разные элементарные проверки из множества П, то алгоритм диагноза называется условным. В условных алгоритмах выбор или назначение некоторых или всех (кроме 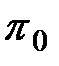) элементарных проверок производится с учетом результатов предыдущей уже реализованной элементарной проверки.

Достоинства безусловных алгоритмов: простота проверок, требуется хранить лишь состав элементарных проверок и единственную последовательность их реализации. Для условных требуется хранить кроме состава элементарных проверок все признаки безусловных и условных переходов от данной элементарной проверки к следующей, т.е. хранить не одну, а несколько последовательностей реализации элементарных проверок.

Безусловные алгоритмы диагноза можно классифицировать по характеру их остановки. Если выдача результатов диагноза предусмотрена только после реализации всех элементарных проверок, то алгоритм является алгоритмом с безусловной остановкой. Таким алгоритмам соответствуют деревья, у которых все висящие вершины имеют один и тот же ранг.

Во многих случаях фактическое техническое состояние объекта может быть определенно с требуемой глубиной диагноза прежде, чем будут реализованы все элементарные проверки алгоритма диагноза. Безусловные алгоритмы, у которых предусмотрена возможность выдачи результатов диагноза после реализации каждой элементарной проверки, называются алгоритмами с условной остановкой. Характерная особенность - не менее двух висящих вершин, ранги которых различны. Все условные алгоритмы являются алгоритмами с условной остановкой. Все указанные типы алгоритмов применяются в системах тестового диагноза. В системах функционального диагноза применяются алгоритмы с условной остановкой в связи с необходимостью немедленного определения неисправного состояния объекта.

Метод Байеса.

Среди методов технической диагностики метод, основанный на обобщенной формуле Байеса, занимает особое место благодаря простоте и эффективности.

Имеет он и недостатки: большой объем предварительной информации, угнетение редко встречающихся диагнозов. Однако в случаях, когда объем статистических данных, позволяет применить метод Байеса, его целесообразно использовать как один из наиболее эффективных и надежных методов.

Основы метода.

Метод основан на простой формуле Байеса. Если имеется диагноз D_i и простой признак k_j, встречающийся при этом диагнозе, то вероятность совместного появления событий (наличие у объекта состояния D_i и признака k_j)

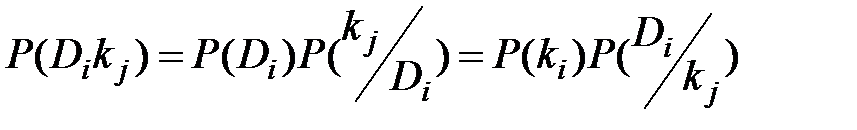. (3.1)

Из этого равенства вытекает формула Байеса

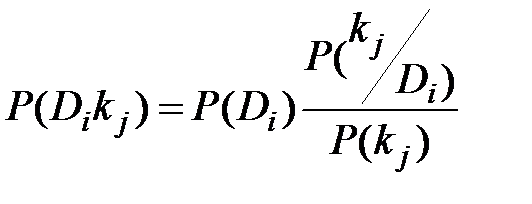. (3.2)

Очень важно определить точный смысл всех входящих в эту формулу величин. 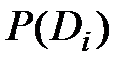- вероятность диагноза D_i, определяемая по статистическим данным (априорная вероятность диагноза). Так, если предварительно обследовано N объектов и у N_i объектов имелось состояние D_i, то

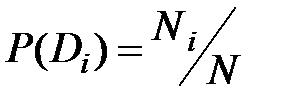. (3.3)

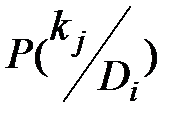вероятность появления признака k_j у объектов с состоянием D_i. Если среди N_iобъектов, имеющих диагноз D_i у N_ij, проявился признак k_j, то

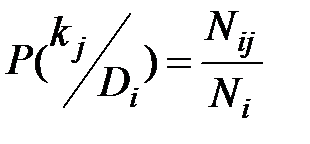. (3.4)

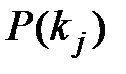- вероятность появления признака k_j во всех объектах независимо от состояния (диагноза) объекта. Пусть из общего числа N объектов признак k_jбыл обнаружен у N_jобъектов, тогда

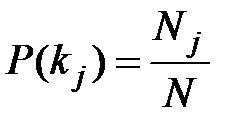. (3.5)

Для установления диагноза специальное вычисление 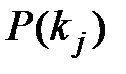не требуется. Как будет ясно из дальнейшего, значения 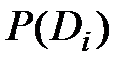, , 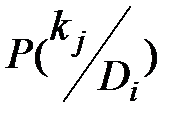известные для всех возможных состояний, определяют величину .

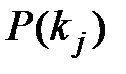В равенстве (3.2) 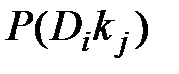- вероятность диагноза D_i после того, как стало известно наличие у рассматриваемого объекта признака k_j (апостериорная вероятность диагноза).

Обобщенная формула Байеса. Эта формула относится к случаю, когда обследование проводится по комплексу признаков K, включающему признаки k₁, k_2, …k_ν. Каждый из признаков k_j имеет m_j разрядов (k_j1, k_j2, …k_js, …, k_jmj). В результате обследования становится известной реализация признака 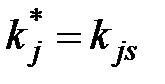и всего комплекса признаков K^*. Индекс * означает конкретное значение (реализацию признака). Формула Байеса имеет вид

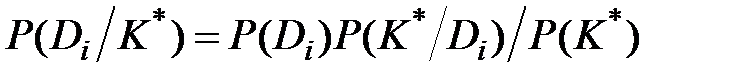, i=1, 2, …, n, (3.6)

где 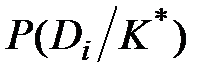- вероятность диагноза D_iпосле того, как стали известны результаты обследования по комплексу признаковК; 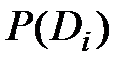- предварительная вероятность диагноза D_i (по предшествующей статистике).

Формула 3.6 относится к любому из n возможных состояний (диагнозов) системы. Предполагается, что система находится только в одном из указанных состояний и потому

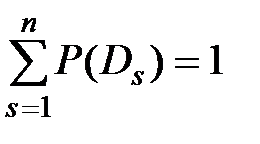. (3.7)

В практике нередко существуют несколько состояний A₁, …A_r, причем некоторые могут встретиться в комбинации друг с другом. Тогда в качестве различных диагнозов D_i следует рассматривать отдельные состояния D₁=A₁,…D_r=A_r и их комбинации D_r+1=A₁^A₂, … и т.п.

Если комплекс признаков состоит из ν признаков, то

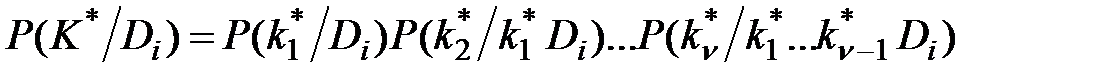, (3.8)

где 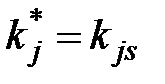- разряд признака, выявившийся в результате обследования.

Для диагностически независимых признаков

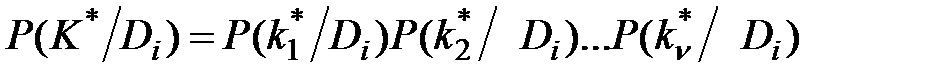. (3.9)

Вероятность появления комплекса признаков K^*

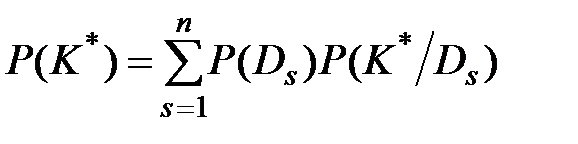. (3.10)

Обобщенная формула Байеса может быть записана

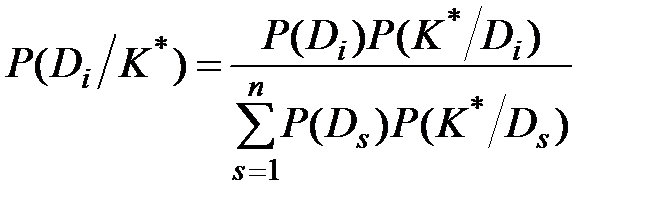, (3.11)

где 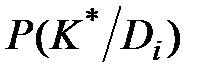определяется равенством 3.8 и 3.9.

Из соотношения 3.11 вытекает 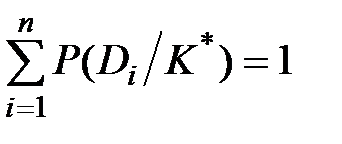, что, разумеется, и должно быть, так как один из диагнозов обязательно реализуется, а реализация двух диагнозов невозможна.

Диагностическая матрица.

Для определения вероятности диагнозов по методу Байеса необходимо составить диагностическую матрицу, которая формируется на основе предварительного статистического материала. В таблице содержатся вероятности разрядов признаков при различных диагнозах. Если признаки двухразрядные (да - нет), то в таблице достаточно указать вероятность появления признака 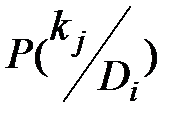. Вероятность отсутствия признака .

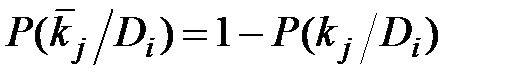В диагностическую матрицу включены априорные вероятности диагнозов.

Диагноз Di	Признаки kj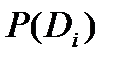
k1	k2	k3
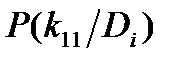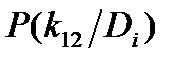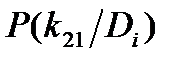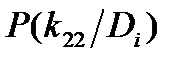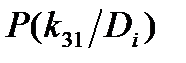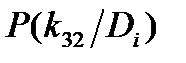D1	0.8	0.2	0.1	0.1	0.2	0.8	0.3
D2	0.1	0.7			0.1	0.9	0.1
…	…	…	…	…	…	…	…

Поясним метод Байеса. Например, при наблюдении за трансформатором проверяются два признака: k₁- повышение температуры обмоток трансформатора и k₂ - уровень шума, создаваемый трансформатором. Предположим, что появление этих признаков связано с неисправностью трансформатора. При нормальном состоянии трансформатора (состояние D₃) признак k₁ не наблюдается, а признак k₂ наблюдается в 5% случаев. На основании статистических данных известно, что 80% трансформаторов вырабатывает ресурс в нормальном состоянии, 5% имеют состояние D₁ и 15% - состояние D₂. известно также, что признак k₁ встречается при состоянии D₁ в 20%, а при состоянии D₂ в 40% случаев; признак k₂ при состоянии D₁ встречается в 30%, а при D₂ в 50% случаев. Сведем данные в диагностическую таблицу.

Di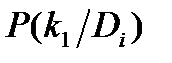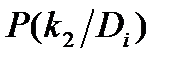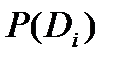
D1 D2 D3	0.2 0.4 0.0	0.3 0.5 0.05	0.05 0.15 0.80

Вероятность состояния, когда обнаружены оба признака определяем по формуле (3.11),

.

,

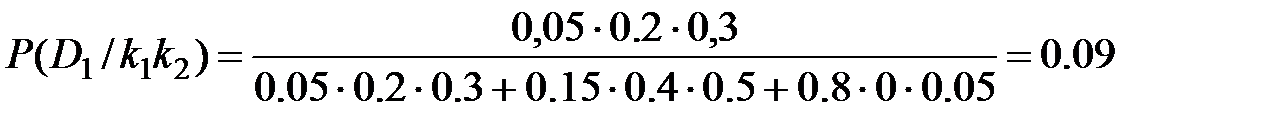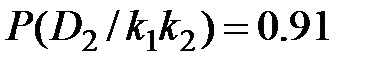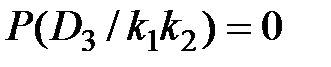
Признак k₁ отсутствует, присутствует признак k₂. Отсутствие признака k₁ есть признак наличия 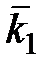(противоположное событие), причем .

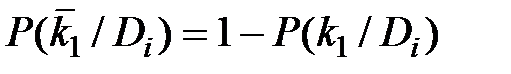Для расчета также применяют формулу (3.11), но 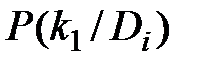заменяют на .

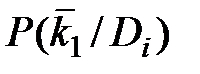Тогда .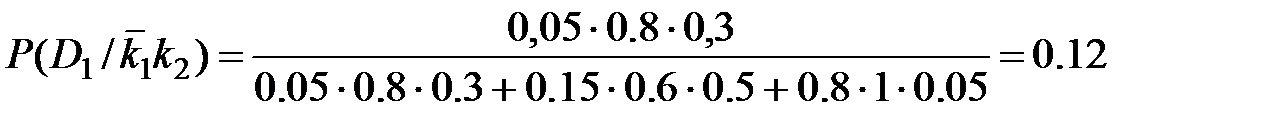

;

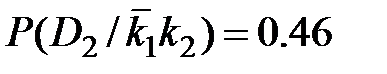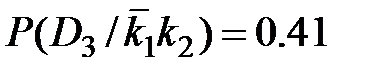
Когда отсутствуют оба признака,

.

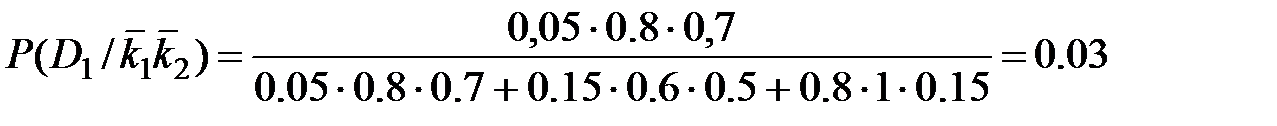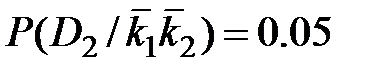
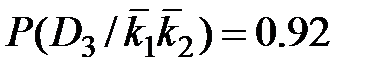
Из проведенных расчетов можно установить, что при наличии двух признаков в трансформаторе с вероятностью 0.91 имеется состояние D₂, т.е. увеличение шума. При отсутствии обоих признаков наиболее вероятно нормальное состояние (вероятность 0.92).Во втором случае, так как вероятности примерно одинаковы, необходимо дополнительное исследование для уточнения состояния трансформатора.

Решающее правило.

Правило, в соответствии с которым принимается решение о диагнозе. В методе Байеса объект с комплексом признаковК^* относится к диагнозу с наибольшей (апостериорной) вероятностью.

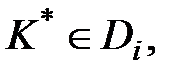если 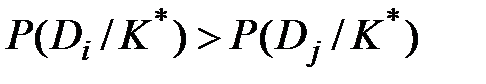, (j=1,2,…n; )

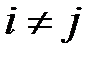Условие указывает, что объект, обладающий данной реализацией комплекса признаковК^*, принадлежит диагнозу (состоянию) D_i. Данное правило уточняется введением порогового значения для вероятности диагноза:

,

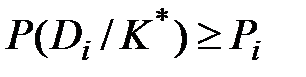где Р_iзаранее выбранный уровень распознавания для диагноза D_i.

При этом вероятность ближайшего конкурирующего диагноза не выше 1-Р_i. Обычно принимается 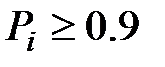. При условии 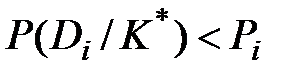решение о диагнозе не принимается (отказ от распознавания) и требуется поступление дополнительной информации.