Метод непосредственнойоценки

Метод непосредственной оценки состоит в том, что диапазон изменения какой – либо количественной переменной разбивается на несколько интервалов, каждому из которых присваивается определенная оценка в баллах, например, от 0 до 10. Начало шкалы – 0 баллов – отсутствие значения параметра. Верхняя же граница шкалы – 10 баллов соответствует наивысшей возможной значительности параметра. Используя подобную шкалу, эксперт должен приписать каждому параметру какое – то числовое значение Pijв пределах используемой им большой шкалы. Затем вычисляется среднее по всем экспертам значение Pi.

Pi =

åPij

j=1 . (9)

N

Величины Piмогут быть использованы для определения коэффициентов весомости и оценки показателей качества.

Чтобы определить коэффициент весомости соблюдается условие åMi= 1, получаем

I=1

Данная операция, носит название нормирования.

Мi =

Pi

n

åPi

i=1

. (10)

Метод парныхсравнений

Матричный метод. Этот метод основан на сравнении объектов экспертизы попарно для установления наиболее важного в каждой паре.

Каждый эксперт получает неполную матрицу, на осях абсцисс и ординат которой расположены сравниваемые параметры (рис. 2 – пример матрицы для случая пяти параметров). Заполняются только те клетки, которые находятся справа от нисходящей диагностики.

В каждой клетке матрицы эксперта просят поставить номер того из двух сравнительных параметров, который, с точки зрения эксперта, является большим (лучшим, наиболее важным).

Метод парных сравнений

К числу наиболее доступных в применении, относятся, например, метод парных сравнений, при использовании которого строится матрица, где на пересечении строки и столбца фиксируются номера тех функций, которые оказываются наиболее важными при попарном сравнении. В таблице 1 приведена оценка функций (F ₁«периодически записывать данные в автоматическом режиме»), (F ₂«устанавливать режим доступа к данным»), (F ₃«периодически копировать данные на жесткий диск») и (F ₄«упорядочивать данные»), реализующих функцию «сохранять данные» в соответствии с фрагментом функциональной модели автоматизированной системы управления техпроцессом.

Таблица 1

Матрица парного сравнения функций

Функции	Функции F i	Количество предпочтений	Значимость
F i	F 1	F 2	F 3	F 4	S i	Hi
F 1	--					0,33
F 2		--				0,17
F 3			--			0,33
F 4				--		0,17

В графу 6 таблицы записываются количества предпочтений S_i, полученных каждой функцией по отношению к остальным (т.е. количество предпочтений i-ой функции, содержащихся в графах 2 - 5 i-й строки), а в графу 7 - значимости функций P_i , рассчитываемые по формуле

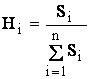, (1)

где n – количество функций в оцениваемом комплексе.

Поскольку при использовании метода парных сравнений величина 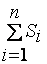, стоящая в знаменателе дроби, т.е. общее возможное число предпочтений, равна (n² - n)/2, то расчет значимости может также производиться по формуле

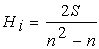. (2)

Кроме метода парных сравнений, возможно также использование для оценки значимости функций метода расстановки приоритетов. В этом случае на первом этапе строится система сравнения функций, включающая символы « > », « < » и « = », обозначающие, соответственно, более высокую, меньшую и примерно равную значимость. Ниже приведен пример такой системы для функций, определенных выше:

F ₁ > F ₂ F ₂ < F₃ F₃ > F ₄

F ₁ < F₃ F ₂ = F ₄

F ₁ > F ₄

Затем на основании полученной системы строится матрица смежности, в которой символы « > », « < » и « = », заменяются коэффициентами предпочтения (в данном случае – соответственно 1,5; 1,0 и 0,5). Пример такой матрицы для показанной выше системы сравнения приведен в следующей таблице.

Таблица 2

Матрица смежности

Функция	Функция F i	Сумма значений	Абсолютный приоритет	Значимость
F i	F 1	F 2	F3	F 4	по строке U i	Ui	Hi
F 1	1,0	1,5	0,5	1,5	4,5	16,25	0,273
F 2	0,5	1,0	0,5	1,0	3,0	11,0	0,185
F3	1,5	1,5	1,0	1,5	5,5	21,25	0,375
F 4	0,5	1,0	0,5	1,0	3,0	11,0	0,185
Итого						59,5

По каждой строке матрицы определяется сумма U_i присвоенных коэффициентов предпочтения. Затем вычисляются абсолютные приоритеты функций U_i , для чего каждая строка в матрице умножается на вектор-столбец U_i. Например, для соотношений, представленных в табл. 2, расчет выглядит следующим образом:

U₁^’ = 1,0 · 4,5 + 1,5 · 3,0 + 0,5 ·5,5 + 1,5 · 3,0 = 16,25;

U₂^’ = 0,5 · 4,5 + 1,0 · 3,0 + 0,5 ·5,5 + 1,0 · 3,0 = 11,0;

U₃^’ = 1,5 · 4,5 + 1,5 · 3,0 + 1,0 ·5,5 + 1,5 · 3,0 = 21,25;

U₄^’ = 0,5 · 4,5 + 1,0 · 3,0 + 0,5 ·5,5 + 1,0 · 3,0 = 11,0;

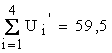
Значимости функций H_i рассчитываются в этом случае исходя из полученных значений их абсолютных приоритетов по формуле

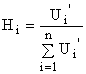. (3)

Сравнительно доступным и быстрым способом оценки значимости функций является также применение упрощенного метода балльной оценки. В этом случае проводится оценка значимости в произвольной системе баллов, после чего H_i рассчитывается по формуле

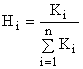, (4)

где K_i – оценка значимости i-й функции в произвольной системе баллов. Пример расчета значимости при помощи упрощенного метода балльной оценки приведен в таблице для случая использования 100-бальной шкалы оценок.

Таблица 3

Балльная оценка значимости функций

Функция F i	Балльная оценка значимости К i	Значимость Н i
F 1		0,357
F 2		0,095
F3		0,476
F 4		0,071

Вне зависимости от способа определения значимости, для полученных результатов должно соблюдаться условие 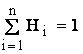(5). Формулы (1)–(5) показывают расчет значимости функций на основании оценок одного эксперта. Реальная же оценка должна проводиться группой экспертов, каждый из которых получает возможность пользоваться любым из приведенных методов. Итоговая значимость i-й функции W_i получается путем усреднения значимостей, полученных при обработке оценок всех экспертов:

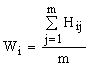, (6)

где H_ij – частный показатель значимости i-й функции, полученный по результатам оценки j-го эксперта; m – число экспертов, принимающих участие в оценке.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1 Соловьев Б. Л. К вопросу определения потребительского эффекта товаров // Управление качеством, эффективностью и совершенствованием ассортимента промышленных товаров. Тез.докл. V Всесоюз. межв. научн. конф. (г. Тбилиси, нояб. 1981г.).

2 Льюис Р. Д., Райфа Х. Игры и решения, М.: "Иностранная литература",1961.

3 Николаева М. А. Товарная экспертиза. М.: "Деловая литература",1998.

4 РайхманЭ.П.,АзгальдовГ.Г.ЭкспертныеметодывоценкекачестватоваровМ.:"Экономика",1974.

5 Акофф Р. Планирование в больших экономических системах. М.: "Советское радио",1972.

6 Ядов В. А. Социологическое исследование. М.: "Наука",1972.

7 Акофф Р., Эмери Ф. О целеустремленных системах. М.: "Советское радио",1974.

8 Оценка качества товаров народного потребления. М.: "Экономика",1972.