Описание связей между макроэкономическими переменными.
Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае линейной двухфакторной модели рассчитываются по формулам
Э ŷх1(х2) = а1х1 / у; Э ŷх2(х1)= а2х2 / у. (3.3)
Частные коэффициенты эластичности показывают, на сколько процентов изменится результативный признак, если изменить один из факторных признаков на один процент не меняя значения остальных.
В рассматриваемом выше примере 3.1
Эŷх1(х2)=0,06815·6080,5/1313,9=0,315; Эŷх2(х1)=380.47·3,1/1313,9=0,898.
Это означает, что при увеличении душевого дохода на один процент и неизменном размере семьи расходы на питание увеличатся на 0,315 процента, а увеличение на один процент (условно) размера семьи при неизменном душевом доходе приведет к росту расходов на питание на 0,898 процента.
Пример3.2. Как размер платы за квартиру зависит от площади квартиры и от количества человек, прописанных в данной квартире.
Данные приведены в табл.3.2.
Таблица 3.2
| N | Квартплата, руб. | Площадь квартиры, м2 | Количество человек |
| y | x1 | x2 | |
| 244,19 | 46,0 | ||
| 450,50 | 80,2 | ||
| 199,86 | 43,8 | ||
| 192,00 | 48,9 | ||
| 98,50 | 12,0 | ||
| 356,59 | 59,8 | ||
| 381,54 | 51,9 | ||
| 118,48 | 18,0 | ||
| 324,40 | 53,8 | ||
| 182,50 | 16,0 | ||
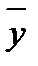 =254,86 =254,86 | 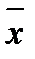 1=43,04 1=43,04 | 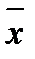 2=2,5 2=2,5 |
Построим линейную аддитивную модель в виде ŷ=а0+а1x1+а2x2. Необходимые данные для расчета модели сведем в табл. 3.3.
Таблица 3.3
| N | yx1 | yx2 | x12 | x22 | x1x2 |
| 11232,74 | 732,57 | ||||
| 36130,1 | 1351,5 | 6432,04 | 240,6 | ||
| 8753,87 | 199,86 | 1918,44 | 43,8 | ||
| 9388,8 | 2391,21 | 97,8 | |||
| 98,5 | 12,0 | ||||
| 21324,08 | 1069,77 | 3576,04 | 179,4 | ||
| 19801,93 | 1526,16 | 2693,01 | 207,6 | ||
| 2132,64 | 236,96 | ||||
| 17452,72 | 973,2 | 2894,44 | 161,4 | ||
| 547,5 | 48,0 | ||||
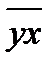 1=13031,9 1=13031,9 | 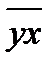 2=712 2=712 | 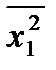 =2274,58 =2274,58 | 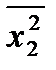 =7,1 =7,1 | х1х 2=116,46 |
Для решения линейной двухфакторной модели строим следующую систему уравнений:
а0+ 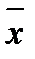 1a1+
1a1+ 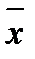 2a2 =
2a2 = 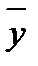
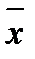 1а0+
1а0+ 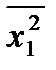 a1+ х1х 2a2 =
a1+ х1х 2a2 = 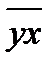 1
1
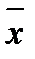 2а0+ х1х 2a1+
2а0+ х1х 2a1+ 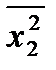 a2 =
a2 = 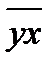 2.
2.
Нам нужно решить систему из трех линейных уравнений с тремя неизвестными и найти значения коэффициентов модели а0, а1 и а2.
Подставляя в данную систему найденные числовые данные, получим систему
а0+43,04 a1+2,5 a2 = 254,86
43,04 а0+2274,58 a1+116,46 a2 = 13031,89
2,5 а0+116,46 a1+7,1 a2 = 712.
Для того чтобы решить данную систему уравнений методом Крамера, найдем сначала значение определителя основной матрицы. Этот определитель определяется равенством
| ∆ = | 43,04 2,5 | 43,04 2274,58 116,46 | 2,5 116,46 7,1 | = 1 | 2274,58 116,46 | 116,46 7,1 | - 43,04 | 43,04 2,5 | 116,46 7,1 |
| + 2,5 | 43,04 2,5 | 2274,58 116,46 | =1×(16149,518-13562,93)-43,04×(305,58-291,1)+2,5× |
×(5012,44–5686,45)=2586,586 – 621,07 – 1685,025=280,49.
Получили, что ∆=280,49≠0, значит, система уравнений имеет единственное решение, которое находится по формулам Крамера
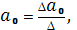
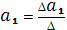 ,
, 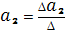 .
.
| ∆а0 = | 254,86 13031,89 | 43,04 2274,58 116,46 | 2,5 116,46 7,1 | = 254,86 | 2274,58 116,46 | 116,46 7,1 | – 43,04× |
| 13031,89 | 116,46 7,1 | + 2,5 | 13031,89 | 2274,58 116,46 | = 254,86×(16149,52-13562,93)- |
- 43,04×(92526,42–82919,52) + 2,5×(1517693,9–1619500,96) = 659218,33 –
– 413480,98–254515,25= –8777,9.
| ∆а1= | 43,04 2,5 | 254,86 13031,89 | 2,5 116,46 7,1 | =1 | 13031,89 | 116,46 7,1 | – 254,86 | 43,04 2,5 | 116,46 7,1 | |||||
| + 2,5 | 43,04 2,5 | 13031,89 | =1×(92526,42–82919,52)–254,86×(305,58–91,15)+2,5× | |||||||||||
×(30644,48–32579,72)=9606,9–3677,63–4838,1=1091,2.
| ∆а2= | 43,04 2,5 | 43,04 2274,58 116,46 | 254,86 13031,89 | = 1 | 2274,58 116,46 | 13031,89 | – 43,04× |
| 43,04 2,5 | 13031,89 | + 254,86 | 43,04 2,5 | 2274,58 116,46 | = 1×(1619500,96–1517693,91) – |
– 43,04 ×(30644,48 – 32579,73) + 254,86 × (5012,44 –5686,45) =
=101807,05+83293,16–171778,19=13322,02.
Теперь мы можем найти значения коэффициентов модели а0, а1 и а2.
а0 = –8777,9/280,49= –31,3;
а1 = 1091,2/280,49= 3,89;
а2 = 13322,02/280,49= 47,5,
следовательно, линейная аддитивная модель имеет следующий вид:
ŷ= –31,3+3,89 x1+47,5 x2.
Коэффициент регрессии модели а1 =3,89 показывает, что каждый метр площади квартиры повышает квартплату на 3,89 руб., а коэффициент а2=47,5 показывает, что каждый прописанный человек повышает квартплату на 47,5 руб.
Найдем теоретические значения ŷ и их отклонения от априорных (данные приведены в табл.3.4).
Таблица3.4
| номер | y | (y - 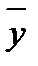 )2 )2 | ŷ | ε=ŷ - у | ε2 |
| 244,19 | 113,85 | 290,14 | 45,9 | 2106,8 | |
| 450,50 | 38275,01 | 423,1 | –27,4 | 750,8 | |
| 199,86 | 186,52 | –13,3 | 176,9 | ||
| 192,00 | 3951,38 | 253,88 | 61,9 | 3831,6 | |
| 98,50 | 24448,45 | 62,88 | –35,6 | 1267,4 | |
| 356,59 | 10348,99 | 343,79 | –12,8 | 163,8 | |
| 381,54 | 16047,82 | 360,61 | –20,9 | 436,8 | |
| 118,48 | 18599,50 | 133,74 | 15,3 | 234,1 | |
| 324,40 | 4835,81 | 320,47 | –3,9 | 15,2 | |
| 182,50 | 5235,97 | 173,5 | –9 | ||
| ∑/n | 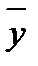 =254,86 =254,86 | 12488,18 | 906,4 |
Совокупный коэффициент детерминации
R2= 1 – 906,4/12488,18= 0,927.
Значение данного коэффициента близко к 1, что очень хорошо.
Формирование регрессионных моделей на компьютере с помощью ППП Excel
Однофакторная регрессия.
Статистическая функцияЛИНЕЙН определяет параметры линейной регрессии у=ах+b. Порядок вычисления следующий:
1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
2) выделите область пустых ячеек 5´2 (5 строк, 2 столбца) длявывода результатов регрессионной статистики или область 1´2 – для получения только оценок коэффициентов регрессии;
3) активизируйте Мастер функций любым из способов:
а) в главном меню выберитеВставка/Функция;
б) на панели инструментовСтандартная щелкните по кнопке Вставка функции;
4) в окне Категория выберитеСтатистические, в окне Функция –ЛИНЕЙН. Щелкните по кнопкеОК;
5) заполните аргументы функции:
Известные_значения_у– диапазон, содержащий данные результативного признака;
Известные_значения_х– диапазон, содержащий данные факторов независимого признака;
Константа - логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щелкните по кнопкеОК;
6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.
Регрессионная статистика представляется в выделенной области в следующем порядке:
| Значение коэффициента a | Значение коэффициента b |
| Среднеквадратическое отклонение a | Среднеквадратическое отклонение b |
| Коэффициент детерминации R2 | Среднеквадратическое отклонение y |
| F-статистика | Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
Многофакторная регрессия.
Построение линейной многофакторной модели производится с помощью инструментов пакета анализа данных Корреляцияи Регрессия. Корреляция используется для расчета матрицы парных коэффициентов корреляции. С помощью Регрессии, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:
1) проверьте доступ к пакету анализа. Пакет анализа представляет собой программу, которая доступна при установке MicrosoftOffice или Excel. Чтобы использовать надстройку в Excel, необходимо сначала загрузить ее. Для версии 2003 в главном меню последовательно выберите Сервис/Надстройки. Установите флажок Пакет анализа, а затем нажмите кнопку ОК.
Для версии 2007 щелкните значок Кнопка MicrosoftOffice  , а затем щелкните Параметры Excel.Выберите команду Надстройки и в окне Управление выберите пункт Надстройки Excel. Нажмите кнопкуПерейти. В окне Доступные надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК. Совет: если Пакет анализа отсутствует в списке поля Доступные надстройки, то для проведения поиска нажмите кнопку Обзор.
, а затем щелкните Параметры Excel.Выберите команду Надстройки и в окне Управление выберите пункт Надстройки Excel. Нажмите кнопкуПерейти. В окне Доступные надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК. Совет: если Пакет анализа отсутствует в списке поля Доступные надстройки, то для проведения поиска нажмите кнопку Обзор.
В случае появления сообщения о том, что пакет статистического анализа не установлен на компьютере и предложения установить его, нажмите кнопкуДа.
2) после загрузки пакета анализа в версии 2003 команда Анализ данных становится доступной в пункте Сервис,а в версии 2007 в группе Анализ на вкладке Данные.
3) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
4) в меню Анализ данных выберите пункт Корреляция;
5) заполните диалоговое окно входных данных и параметров вывода:
Входной интервал – диапазон, содержащий анализируемые данные (все столбцы или строки);
Группирование – по столбцам или по строкам;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Выходной интервал – достаточно указать левую верхнюю ячейку диапазона;
6) результаты вычислений – матрица парных коэффициентов корреляции, анализ которых позволяет выполнить первый этап процесса моделирования, описанный в 2.4;
7) в меню Анализ данных выберите пункт Регрессия;
8) заполните диалоговое окно входных данных и параметров вывода как в пункте 4, только интервал для результативного признака Y и для факторов Х надо задавать отдельно (причем входной интервал Х должен включать все столбцы, содержащие значения факторных признаков);
9) в результате получаем регрессионную статистику, таблицу дисперсионного анализа и таблицу коэффициентов модели, в которой первая строка (Y-пересечение) соответствует коэффициенту а0, а следующие строки описывают коэффициенты регрессии аi.В 4 столбце находятся коэффициенты t-статистики, определяющие достоверность вычисленных коэффициентов регрессии: t=1 соответствует примерно 70% достоверности, t=2 соответствует примерно 95% достоверности,t=3 соответствует примерно 100% достоверности.
3.6. Практический блок
Примеры
Задача 1. В таблице указаны парные коэффициенты корреляции. Проведите анализ целесообразности включения заданных факторов в уравнение множественной линейной регрессии.
| y | x1 | x2 | x3 | x4 | |
| y | |||||
| x1 | 0,71 | ||||
| x2 | 0,58 | 0,53 | |||
| x3 | 0,08 | 0,2 | 0,13 | ||
| x4 | 0,62 | 0,81 | 0,3 | 0,25 |
РЕШЕНИЕ. Между y и x3 связь практически отсутствует. Между y и x1 связь сильная, между y и x2, x4 – умеренная.
Отсюда следует вывод о нецелесообразности включения фактора x3 в уравнение множественной линейной регрессии (коэффициент парной корреляции су равен 0,08).
Между факторами x1 и x4 существует сильная прямая связь (коэффициент парной корреляции > 0,8). Для того, чтобы избежать явления мультиколлинеарности, один из этих факторов должен быть исключен из анализа. Исключается фактор x1, умеренно коррелирующий с x2 (коэффициент их парной корреляции равен 0,53).
Факторы, включенные в модель множественной регрессии: x2, x4.
Задача 2. Построить линейную множественную регрессию общей суммы налогов и платежей на сумму поступлений по налогу на добавленную стоимость (x1) и налогу на прибыль (доход) (x2).
| Время наблюдения | y, млрд. руб. | x1, млрд. руб. | x2, млрд. руб. |
| январь | 38,9 | 5,6 | 13,4 |
| февраль | 45,3 | 6,7 | 15,4 |
| март | 61,1 | 13,1 | 16,7 |
| I квартал | 145,3 | 25,3 | 45,5 |
| апрель | 70,4 | 16,9 | 16,2 |
| май | 63,8 | 18,4 | |
| июнь | 67,7 | 19,1 | |
| II квартал | 201,9 | 54,4 | 44,2 |
| I полугодие | 347,2 | 79,8 | 89,7 |
| июль | 70,6 | 16,1 | 20,8 |
| август | 78,9 | 23,3 | 16,4 |
| сентябрь | 73,2 | 19,2 | 17,4 |
| III квартал | 222,7 | 58,6 | 54,6 |
| 9 месяцев | 569,9 | 138,3 | 144,3 |
| октябрь | 78,1 | 16,1 | 23,6 |
| ноябрь | 31,8 | 23,9 | |
| декабрь | 133,4 | 35,4 | 34,4 |
| IV квартал | 314,5 | 83,3 | 81,9 |
| IIполугодие | 537,2 | 141,9 | 136,5 |
| январь-декабрь | 884,4 | 221,6 | 226,1 |
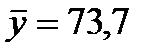 | 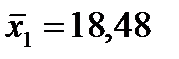 | 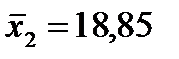 |
а0=-9.7
а1=1.84
а2=2.62
Полученное уравнение
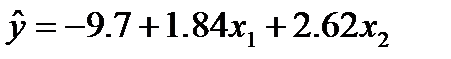
Контрольные вопросы
1. Что понимается под множественной регрессией?
2. Какие задачи решаются при построении уравнения регрессии?
3. Какие задачи решаются при спецификации модели?
4. Какие требования предъявляются к факторам, включаемым в уравнение регрессии?
5. Что понимается под коллинеарностью и мультиколлинеарностью факторов?
6. Как проверяется наличие коллинеарности и мультиколлинеарности?
7. Какие подходы применяются для преодоления межфакторной корреляции?
8. Какие функции чаще используются для построения уравнения множественной регрессии?
9. Какой вид имеет система нормальных уравнений метода наименьших квадратов в случае линейной многофакторной регрессии?
10. По какой формуле вычисляется индекс множественной корреляции?
11. Как вычисляются индекс множественной детерминации и скорректированный индекс множественной детерминации?
12. Что означает низкое значение коэффициента (индекса) множественной корреляции?
13. Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
14. Как строятся частные уравнения регрессии?
15. Как вычисляются средние частные коэффициенты эластичности?
16. Что такое стандартизированные переменные?
17. Какой вид имеет уравнение линейной регрессии в стандартизированном масштабе?
18. Как оценивается информативность (значимость) факторов?
19. Как вычисляются частные коэффициенты корреляции?
20. Опишите процедуру метода исключения переменных с использованием частных коэффициентов корреляции.
21. Какой показатель характеризует долю объясненной с помощью регрессии дисперсии в общей дисперсии зависимой переменной?
22. Из каких этапов состоит проверка качества оцененного уравнения регрессии?
23. Как рассчитывается и что показывает коэффициент детерминации R2?
24. В каких задачах эконометрики используется распределение Фишера?
25. Таблицы каких распределений используются при оценке качества линейной регрессии?
26. Какие показатели характеризуют независимость отклонений зависимой переменной от линии регрессии? Как осуществляется проверка этой независимости?
27. В каких случаях возникают трудности использования множественной линейной регрессии в моделировании? В чем реальная ситуация может не соответствовать предпосылкам модели?
28. Когда необходимо выведение из рассмотрения незначимых объясняющих переменных и добавление новых переменных?
Задания и задачи
1.Имеются данные по 10 фирмам, продающим компакт-диски, – объемы продаж, тыс. шт. / мес. (y), цены, руб. (x1), вложения в рекламу, тыс. руб. / мес. (x2).
| y | ||||||||||
| x1 | ||||||||||
| x2 |
А) Построить регрессионную зависимость 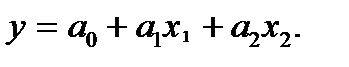
Б) Проверить гипотезу о значимости коэффициентов регрессии при уровнях значимости 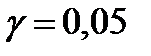 и
и 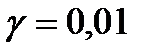 .
.
В) Построить доверительные интервалы для коэффициентов регрессии а0, а1, а2 с вероятностью 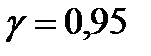 .
.
Г) Вычислить множественный коэффициент корреляции, проверить гипотезу о значимости модели при уровнях значимости 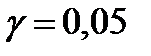 и
и 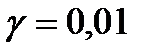 .
.
2. Известны данные: 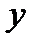 – цена квартиры, x1 – общая площадь, x2– площадь кухни.
– цена квартиры, x1 – общая площадь, x2– площадь кухни.
| y | x1 | x2 |
| 31,5 | 6,2 | |
| 31,8 | 5,6 | |
| 48,8 | 7,9 | |
| 5,6 | ||
| 7,2 | ||
| 6,8 | ||
| 6,5 | ||
А) Построить регрессионную зависимость 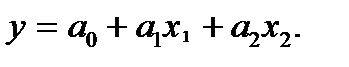
Б) Проверить гипотезу о значимости коэффициентов регрессии при уровнях значимости 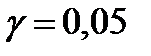 и
и 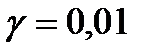 .
.
В) Построить доверительные интервалы для коэффициентов регрессии а0, а1, а2 с вероятностью 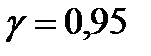 .
.
Г) Вычислить множественный коэффициент корреляции, проверить гипотезу о значимости модели при уровнях значимости 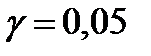 и
и 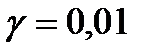 .
.
3. Имеются данные по ценам на квартиры, тыс.руб. (y) в зависимости от общей площади, м2 (x1) и площади кухни, м2 (x2).
А) Построить регрессионную зависимость 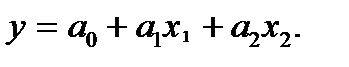
Б) Обосновать наличие гетероскедастичности.
В) С помощью обобщенного метода наименьших квадратов построить зависимость с учетом гетероскедастичности.
| y | ||||||||||
| x1 | ||||||||||
| x2 |
4. Имеются данные по странам за год.
| Страна | Душевой доход, долл., y | Индекс человеческого развития (ИЧР),x1 | Индекс человеческой бедности (ИЧБ),x2 |
| ОАЭ | 0,866 | 14,9 | |
| Таиланд | 0,833 | 11,7 | |
| Уругвай | 0,883 | 11,7 | |
| Ливия | 0,801 | 18,8 | |
| Колумбия | 0,848 | 10,7 | |
| Иордания | 0,730 | 10,9 | |
| Египет | 0,514 | 34,8 | |
| Марокко | 0,566 | 41,7 | |
| Перу | 0,717 | 22,8 | |
| Шри-Ланка | 0,711 | 20,7 | |
| Филиппины | 0,672 | 17,7 | |
| Боливия | 0,589 | 22,5 | |
| Китай | 0,626 | 17,5 | |
| Зимбабве | 0,513 | 17,3 | |
| Пакистан | 0,445 | 46,8 | |
| Уганда | 0,328 | 41,3 | |
| Нигерия | 0,393 | 41,6 | |
| Индия | 0,446 | 36,7 |
Индекс человеческого развитияобъединяет три показателя: валовой внутренний продукт на душу населения, уровень грамотности и продолжительность жизни.
Индекс человеческой бедности определяется как средневзвешенное абсолютного (<1.5 $ на душу) и относительного (<3 $ на душу) индекса бедности.
Задание:
Постройте линейное уравнение множественной регрессии и поясните экономический смысл его параметров.
Рассчитайте частные коэффициенты эластичности.
Определите коэффициенты регрессии.
Сделайте вывод о силе связи результата и факторов.
Определите парные коэффициенты корреляции, сделайте выводы.
Дайте оценку полученного уравнения на основе коэффициента детерминации.
Тесты
1. Значимость частных и парных коэффициентов корреляции проверяется с помощью:
а) нормального закона распределения;
б) t-критерия Стъюдента;
в) F–критерия;
г) таблицы Фишера – Иейтса.
2. В регрессионном анализе x j рассматриваются как:
а) неслучайные величины;
б) случайные величины;
в) любые величины.
3.Коэффициент регрессии изменяется в пределах от
a) –1 до 1,
б) 0 до 1,
в) принимает любое значение.
4.Квадратичная форма
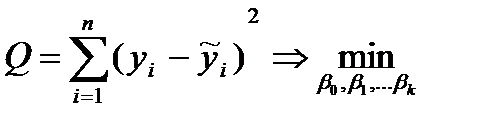
соответствует
a) методу максимального правдоподобия,
б) методу наименьших квадратов,
в) методу средней связи,
г) двухшаговому методу наименьших квадратов.
5.В каких пределах изменяется коэффициент детерминации
a) от 0 до 1,
б) от –1 до 0,
в) от –1 до 1,
г) от 0 до 10.
6.В хорошо подобранной модели остатки должны:
a) иметь нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией,
б) не коррелировать друг с другом,
в) иметь экспоненциальный закон распределения,
г) хаотично разбросаны,
д) форма и вид распределения не важен.
7.Неправильный выбор функциональной формы или объясняющих переменных называется
a) ошибками спецификации,
б) ошибками прогноза,
в) гетероскедастичностью.
8.Коэффициент детерминации это
a) квадрат парного коэффициента корреляции,
б) квадрат частного коэффициента корреляции,
в) квадрат множественного коэффициента корреляции.
9.Квадрат какого коэффициента указывает долю дисперсии одной случайной величины, обусловленную вариацией другой
a) коэффициент детерминации,
б) парный коэффициент корреляции,
в) частный коэффициент корреляции,
г) множественный коэффициент корреляции.
10.Величина, рассчитанная по формуле
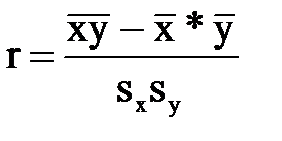 является оценкой
является оценкой
a) коэффициента детерминации,
б) парного коэффициента корреляции,
в) частного коэффициента корреляции,
г) множественного коэффициента корреляции.
11. Выборочный коэффициент корреляции r по абсолютной величине
a) не превосходит единицы,
б) не превосходит нуля,
в) принимает любые значения.
12. Отметьте основные виды ошибок спецификации
a) отбрасывание значимой переменной,
б) добавление незначимой переменной,
в) низкое значение коэффициента детерминации,
г) выбор неправильной формы модели.
13. Компоненты вектора 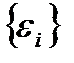
a) независимы между собой,
б) зависимы между собой,
в) имеют нормальный закон распределения с нулевым математическим ожиданием ( 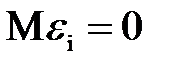 ) и неизвестной дисперсией
) и неизвестной дисперсией 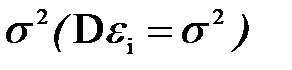 .
.
14. На практике при построении регрессионных моделей рекомендуется, чтобы n превышало т не менее, чем
a) в два раза,
б) в три раза,
в) не имеет значения.
3.7. Самостоятельная работа студентов
Литература для самостоятельной работы
1. Эконометрика: учебник / К. В. Балдин, В. Н. Башлыков, Н. А. Брызгалов и др.; под ред. В. Б. Уткина. -М.: Дашков и К, 2008. -304 с.
2. Афанасьев, В. Н. Эконометрика: учеб. для вузов / В. Н. Афанасьев, М. М. Юзбашев, Т. И. Гуляева ; под ред. В. Н. Афанасьева. -М. : Финансы и статистика, 2006. -255 с.
3. Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А. Эконометрия. Новосибирск, 2003.
Интернет-ресурсы:
1.http://www.kgtu.runnet.ru/WD/TUTOR/textbook/modules/stmulreg.html
2. http://www.shpargalka.ru/statis.ru/doc/shpr_e31.htm
3.http://dsmu.donetsk.ua/~statbook/modules/stmulreg.html#cunique
4. http://www3.unicor.ac.ru/d024/p011993.htm
5. http://www.gauss.ru/educat/systemat/butenkov/.asp
6.http://crow.academy.ru/econometrics/seminars_/sem_08_/sem_08.htm
7.http://crow.academy.ru/econometrics/lectures_/lect_03_/index.htm
8. http://u-pereslavl.botik.ru/UP/ECON/econometrics/
