Связь между элементами моделей задач двойственной пары. Соответствие между переменными двойственных задач.

Связь между элементами моделей задач двойственной пары. Соответствие между переменными двойственных задач.

В пару взаимнодвойственных симметричных задач

f=(n;A=1)Σcj*xj-maxP= (m;i=1)Σbi*xi - min

(n;j=1)Σaij*xj<=bji=1,m (m;i=1)Σaij*yi>=cjj=1,n

Xj>=0, j=1,nyi>=0 i=1,m

Вводим дополнительные переменные и приводим их к каноническому виду:

f=(n;j=1)Σ- maxP= (m;i=1)Σbi*xi –min

(n;j=1)Σaij*xj+xn+1=bii=1,m (m;i=1)Σaij*yi-ym+y=cjj=1,n

Xj>=0 j=1,nyi>=0, i=1,m

Xn+1>=0 i=1,mym+j>=0 j=1,n

Между переменными прямой двойственной задачи можно установить соответствие:

Х1X2 ….. XnXn+1 Xn+2 …. Xn+m

Уm+1 Ym+2 ….. Ym+n Y1 Y2 …. Yn

Это соответствие можно сформировать словесно: основным переменным исходной задачи ставятся дополнительные переменные двойственной задачи, а дополнительным переменным исходной ставятся в соответствие основные двойственные.

Первая теорема двойственности.

Теорема: если одна из двойственных задач имеет оптимальный план, то и другая решима, т.е. имеет опт.план. При этом экстремальные значен.целевых функций совпадают (j=от 1 до n) Σcjxj*= (i=от 1 до m)Σbiyi* если в исходн. задаче целевая функция неограниченна на множестве планов, то в двойственной задаче система ограничений несовместна.

Если для некот-х допустимых планов x* и y* пары двойств-х задач выполн-сярав-во z(x*)=f(y*),то x* и y* явл-сяоптим-ми планами соотв-их задач.Доказ-во:Согласноосн-мунерав-вудвойств-ти, для люб. допуст-го плана х прямой задачи и допуст-го плана y* двойст-й справ-во нерав-во z(x)≤f(y*).Но по условию z(x*)=f(y*). Отсюда в силу транзит-тиотн-й ≤ и = получим z(x)≤z(x*).Т. к. х—произвол-й план,то z(x*)=maxZ .т. е. x*—оптим-й план прямой ЗЛП.Аналог-но доказыв-ся,что план y* явл-сяоптим-м для двойствен-й задачи.

Третья теорема двойственности и ее эконом.интерпритация.

Теорема (об оценках): двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена, соотв.ограничения двойственной задачи.

yi*= Δf max /Δ bi i=1, m илиyi*=(f max)’ bi

yi*= Δf max / Δ bi

Δ f max = Δbiyi*

если Δ bi=1, то Δfmax = yi* следовательно стоимост.оценкарес-са показ-т, как изменится выручка, если кол-во рес-саувелич-ся на единицу.

Интервал устойчивости двойственных оценок.

Двойственные оценки справедливы в допустимом интервале устойчивости, к-рый для ресурса pl, l=1,m имеет вид [bl+Δbl ;bl+Δbl ] , где Δbl – нижний придел уменьшения соответствующего рес-са; Δbl – верхний предел увеличения.

Эти величины (придел измен-ияколич.рес-сов) опред-ся по матрице обратной к матрице коэф-тов ограничений.

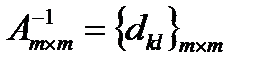
По формулам 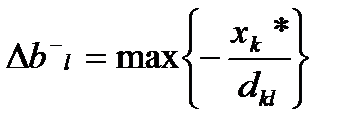dkl>0

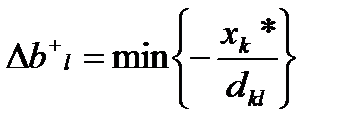
dkl<0

Основное неравенство теории двойственности.

Теорема:Для люб. Допустимых планов х=(х;...;xn) и y=(y;...;ym)

прямой и двойств-й ЗЛП справедливо нерав-во: z(x)≤f(y),

т. е.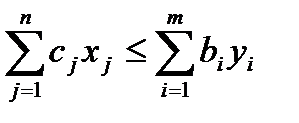

Доказ-во: учитывая нерав-ва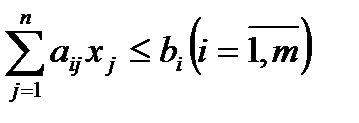

и 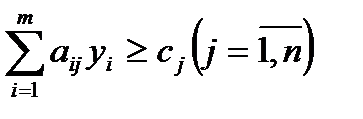, получаем

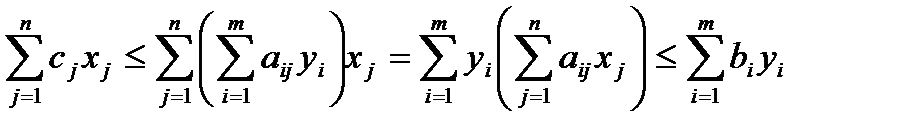, т. е. имеем нерав-во, кот.наз-сяосн-ымнерав-ом теории двойственности.

Связь между элементами моделей задач двойственной пары. Соответствие между переменными двойственных задач.

В пару взаимнодвойственных симметричных задач

f=(n;A=1)Σcj*xj-maxP= (m;i=1)Σbi*xi - min

(n;j=1)Σaij*xj<=bji=1,m (m;i=1)Σaij*yi>=cjj=1,n

Xj>=0, j=1,nyi>=0 i=1,m

Вводим дополнительные переменные и приводим их к каноническому виду:

f=(n;j=1)Σ- maxP= (m;i=1)Σbi*xi –min

(n;j=1)Σaij*xj+xn+1=bii=1,m (m;i=1)Σaij*yi-ym+y=cjj=1,n

Xj>=0 j=1,nyi>=0, i=1,m

Xn+1>=0 i=1,mym+j>=0 j=1,n

Между переменными прямой двойственной задачи можно установить соответствие:

Х1X2 ….. XnXn+1 Xn+2 …. Xn+m

Уm+1 Ym+2 ….. Ym+n Y1 Y2 …. Yn

Это соответствие можно сформировать словесно: основным переменным исходной задачи ставятся дополнительные переменные двойственной задачи, а дополнительным переменным исходной ставятся в соответствие основные двойственные.