Частные производные первого порядка

Полный дифференциал.

Определение 6. Частной производной попеременной «х» от функции 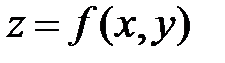называется предел отношения частного приращения 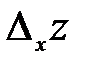к приращению 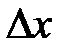при стремлении последнего к нулю.

Частная производная по х обозначается одним из символов

, , .

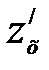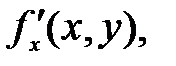
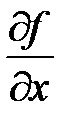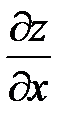Согласно определению

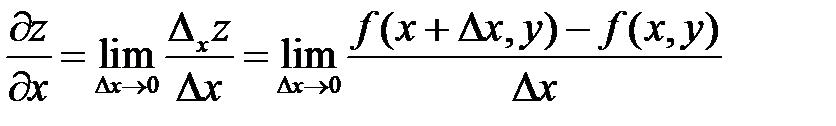. (6)

Определение.7. Частной производной по у от функции 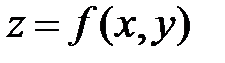называется предел отношения частного приращения 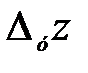к приращению 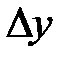при стремлении последнего к нулю.

Частная производная по у обозначается символами

, , , .

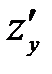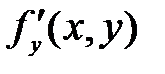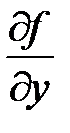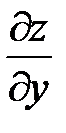Согласно определению

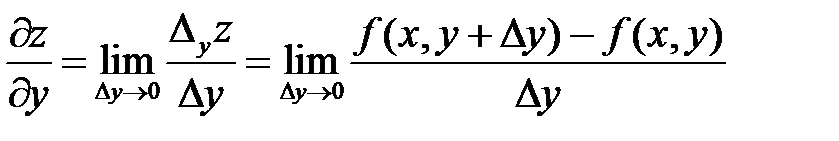. (7)

Из этих определений следует правило, по которому следует вычислять частную производную.

Частная производная 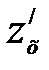вычисляется от функции 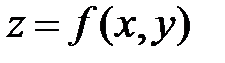по переменной х при постоянной у.

Частная производная 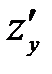вычисляется по переменной у при постоянной х.

При вычислении частных производных применяют все приемы вычислений производных сложных функций.

Пример 4. Вычислить частные производные функции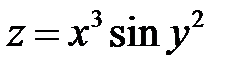

Решение.

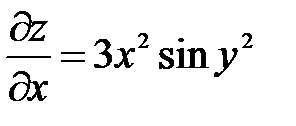– здесь 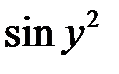играет роль постоянного множителя,

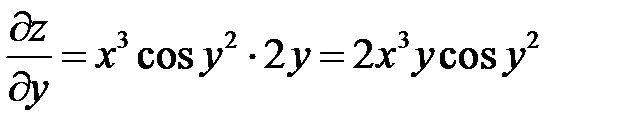– в данном случае 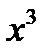числовой множитель, а производную от 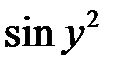вычисляем «по цепочке».

Пример 5. Вычислить частные производные функции .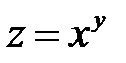

Решение.

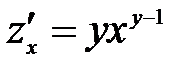, вновь переменная «у» равна постоянной, и мы использовали формулу производной степенной функции .

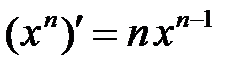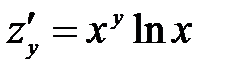, потому что 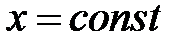, и мы используем формулу производной показательной функции .

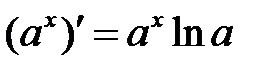Пример 6. Вычислить частные производные функции трех переменных .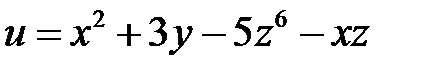

Решение.

, , .

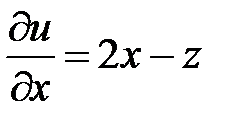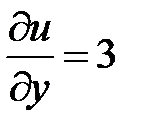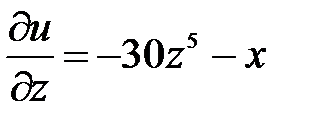Физический смысл частных производных остается прежним: они характеризуют скорость изменения функции по переменным «х» и «у» отдельно.

С геометрической точки зрения производная функции одной переменной численно равна тангенсу угла наклона касательной к положительному направлению оси OХ.

Для функции двух переменных касательная «переходит» в касательную плоскость к поверхности, определяемой уравнением .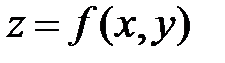

Для функций, содержащих большее число переменных, геометрическую интерпретацию частных производных дать нельзя.

ПДифференциал

Возникает вопрос, а не существует ли одной, общей производной для функции двух или больше аргументов? Нет, не существует. Но общее изменение функции можно охарактеризовать с помощью полного дифференциала 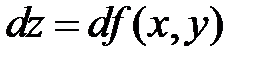, как главной части приращения функции. Для функции одной переменной 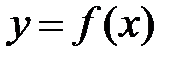дифференциал равен 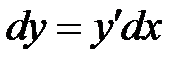. Для функции двух переменных логично ожидать сумму «частных дифференциалов» по обеим переменным. Строгое доказательство этого утверждения можно найти в рекомендуемой литературе. Мы ограничимся определением и покажем его применение для решения задач.

Определение 8 . Пусть функция 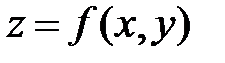непрерывна вместе со своими частными производными по х и у. Полным дифференциалом 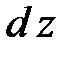называется сумма произведений частных производных на дифференциалы соответствующих независимых переменных, т.е.

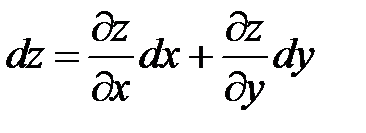. (.8)

Это выражение является аналогом формулы для дифференциала функции одной переменной. Известно, что дифференциал функции приближенно равен ее приращению: 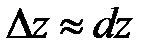. Поэтому значение функции в точке 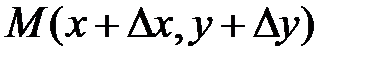можно определить из приближенного равенства:

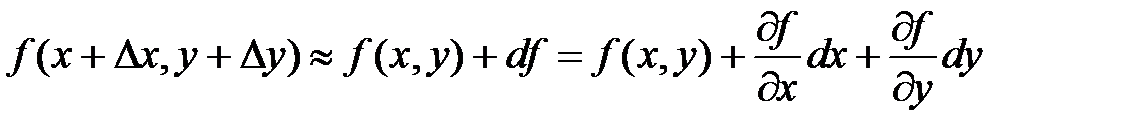, (.9)

где dx и dy – приращения аргументов «х» и «у» соответственно.

Пример 7. Найти полный дифференциал «dz» и полное приращение

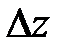« » для функции 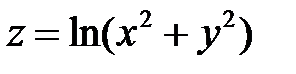, если координаты начальной и конечной точек

М₀( 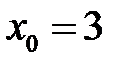, ,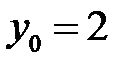) и М₁( ,

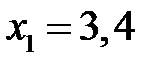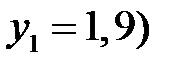
Решение. Найдем значения функции в заданных точках:

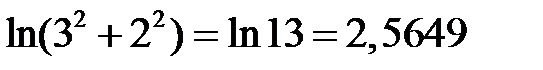и .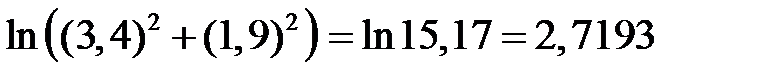

по таблице логарифмов или при помощи калькуляторов. Определим приращение функции:

.

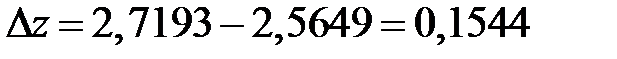Найдем дифференциалы аргументов, как их приращения:

, .

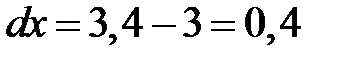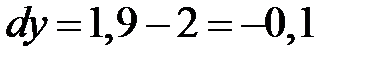Тогда ,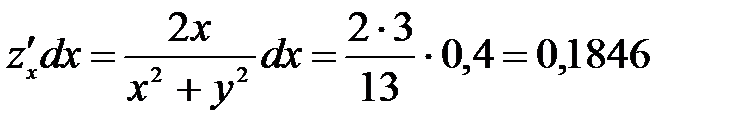

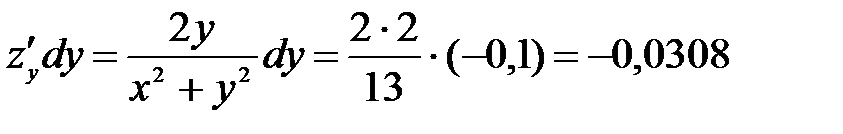
и, окончательно, получаем

.

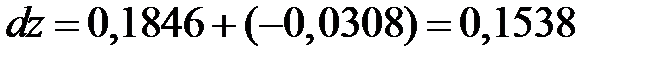Сравним приращение и дифференциал по их разности:

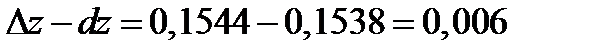, т.е. они мало отличаются друг от друга. Поэтому в вычислениях можно использовать формулу 9:

.

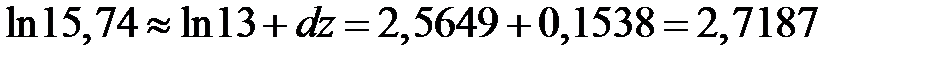Найдем относительную погрешность вычислений:

,

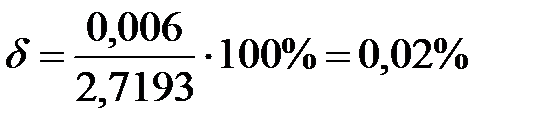что говорит о достаточной степени точности проведенных вычислений.

В разных точках функция имеет различные значения частных производных, поэтому дифференциалы будут разными. По ним можно судить о степени возрастания и убывания функции.