Решение систем уравнений в MathCAD

ВАРИАНТ 2

Отчет лабораторной работы должен представлять собой файл документа MathCAD, сохраненный в папке с названием группы. Имя файла должно соответствовать фамилии студента с указанием номера лабораторной работы. Документ MathCAD должен начинаться с выровненного по центру заголовка «Лабораторная работа №» с указанием номера лабораторной работы. Под заголовком указывается название работы. В последующих строках с выравниванием по левому краю документа указываются группа и фамилия студента, выполнившего работу, и фамилия преподавателя, проверявшего отчет. Образец оформления заголовка лабораторной работы представлен ниже:

Лабораторная работа № 5

Решение систем уравнений в MathCAD

Выполнил: студент гр. ХТ-ТПП-02-1 Иванов Иван Иванович

Проверил: Иванова Наталья Игоревна

Задание 1.

Требуется найти определители матриц коэффициентов и решить в матричной форме следующие системы линейных уравнений:

3.2x - 1.5y + 0.5z = 0.90

1.6x + 2.5y - 1.0z = 1.55

1.0x + 4.1y - 1.5z = 2.08

2x + 6y - z = - 12

5x - y + 2z = 29

- 3x - 4y + z = 5

2x + y - 0.1z + u = 2.7

0.4x + 0.5y + 4z - 8.5u = 21.9

0.3x - y + z + 5.2u = - 3.9

x + 0.2y + 2.5z - u = 9.9

26.38 + 0.15x = - (2.11y + 30,75z)

2.05z + 0.64x = 1.01 - 1.21y

0.53y + 1.04z = 5.23 - 3.21x - y

(5.34 – а) ∙ x + 2.83y + 7.63z = 7.21 - β

6.52y - 5.35x+(2.84 +α)∙ z = 4.22 + β

2.36x - 2.35z = 10.35+(α- 6.74) ∙ y,

гдеα = 0.8, β = 0.4.

Задание 2.

1. В матричной форме требуется рассчитать материальный баланс ректификационной колонны и определить расходы потоков F₁, R₁, R₂ и W. Материальный баланс может быть описан следующей системой линейных уравнений:

F₁ + F₂ = D + R₁ + R₂ + W

0.3F₁+ 0.25F₂= 0.92D + 0.06R₁+ 0.06R₂+ 0.02W

0.2F₁+ 0.25F₂= 0.03D + 0.8R₁+ 0.07R₂+ 0.03W

0.3F₁+ 0.25F₂= 0.03D + 0.07R₁+ 0.8R₂+ 0.03W

0.2F₁+ 0.25F₂= 0.02D + 0.07R₁+ 0.07R₂+ 0.92W,

где F₁ = 3т/ч; D=2т/ч.

В данной системе уравнений больше, чем неизвестных переменных,поэтому одно уравнение можно не использовать в расчете. Перед началом расчета рекомендуется проверить определитель матрицы коэффициентов на возможность получения решения системы.

2. Требуется решить следующие системы уравнений:

cos(0.4y+ x²) + x²+y² - 1.6 = 0

1.5x² - (y² /0.36) - 1 = 0

x= lg(y/z) + 1

y= 0.4 +z² - 2x²

z = 2 +xy/20

Задание 3.

Жидкость из питающей емкости с давлением P₁=0,8 кгс/см нагнетается насосом в трубопровод длиной L₁=20 м и диаметром d=0.05 м.На линии трубопровода имеются местные сопротивление с суммарным коэффициентом Σζ₁ =15. Пройдя трубопровод, нагнетаемая жидкость разделяется на два потока. Первый потока через трубопроводдлинойL₂=18 м, диаметром d=0.05 м и местными сопротивлениями Σζ₂ =5 нагнетается в приемную емкость, находящуюся под давлением P₂=3 кгс/см и установленную на высоте H₂=5 м. Второй поток через трубу с L₃=10 м, d=0.05 и Σζ₃ =7, подается на высоту H₃=7 м в емкость с давлением P₃=3.5 кгс/см². Требуется рассчитать скорости потоков в трех трубопроводах (w₁, w₂ и w₃), а также пьезометрический напор в узловой точке (h₀), если напор насоса Н_Н равен 25 м.

Система трубопроводов описывается следующими уравнениями:

h₀=P₁/g+Н_Н-h₁

H₂+ P₂/ g = h₀- h₂

H₃+P₃/g=h₀-h₃

w₁ = w₂+ w₃

где h₁, h₂ и h₃ – потери напора в трубопроводах, м; ρ – плотность жидкости (ρ = 1000 кг/м³ ), g – ускорение свободного падения (g = 9.81 м/с ).

Потери напора в трубопроводах (h₁, h₂ и h₃) зависят от скоростей движения жидкости в них (w₁, w₂ и w₃) и рассчитываются по следующим уравнениям:

Потери напора в трубопроводе: ;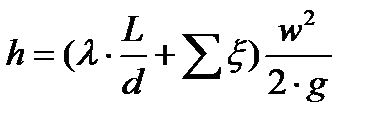

Коэффициент трения: ;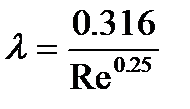

Число Рейнольдса: .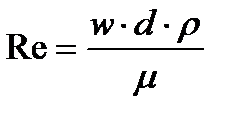

где µ – вязкость жидкости (µ = 10 Па·с).

При выполнении данного задания рекомендуется потери h₁, h₂ и h₃задать как функции от соответствующих скоростей (w₁, w₂ и w₃) и отличающиеся друг от друга только длинами трубопроводов L и коэффициентами сопротивления Σζ.

Задание 4.

1. Для вышеприведенной системы уравнений на одной диаграмме требуется построить графики зависимостей скорости жидкости в трубопроводах (w₁, w₂ и w₃) от напора насоса Н_Н. Диапазон построения графиков выбрать самостоятельно.

2. Как преобразовать систему линейных уравнений в ее матричный вид?

3. Как рассчитать систему линейных уравнений в MathCAD?

4. Как задаются равенства и неравенства в блоке Given … Find( )?

5. Использование функции Find( ) в составе других функций.