Решение уравнений с одним неизвестным в MathCAD

ВАРИАНТ 1

Отчет лабораторной работы должен представлять собой файл документа MathCAD, сохраненный в папке с названием группы. Имя файладолжно соответствовать фамилии студента с указанием номера лабораторной работы. Документ MathCAD должен начинаться с выровненного по центру заголовка «Лабораторная работа №» с указанием номера лабораторной работы. Под заголовком указывается название работы. В последующих строках с выравниванием по левому краю документа указываются группа и фамилия студента, выполнившего работу, и фамилия преподавателя, проверявшего отчет. Образец оформления заголовка лабораторной работыпредставлен ниже:

Лабораторная работа № 4.1.

Решение уравнений с одним неизвестным в MathCAD

Выполнил: студент гр. ХТ-ТПП-02-1 Иванов Иван Иванович

Проверил: Иванова Наталья Игоревна

Задание 1.

Для следующих уравнений требуется графически оценить их решения и уточнить значения неизвестных переменных при помощи стандартной функции root( ):

.

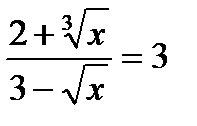
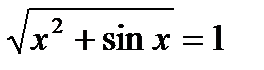
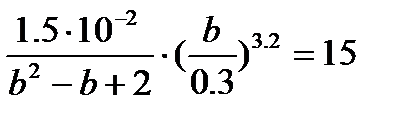
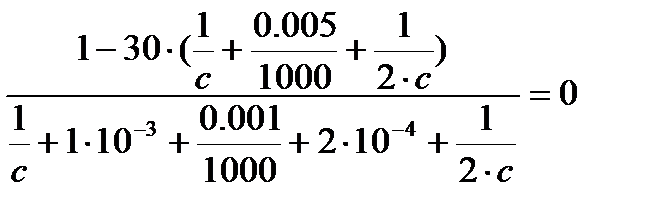
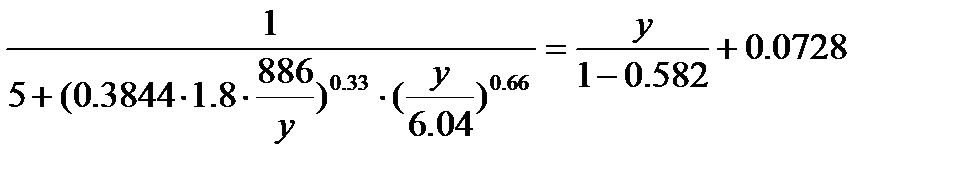Задание 2.

Жидкость по трубе самотеком перетекает из одной емкости в другую только за счет разности давлений в них. Давление в приемной емкости равно атмосферному. При помощи функции root( ) требуется вычислить скорости течения жидкости в трубе w, м/с при избыточных давлениях в первой емкости P₁ равных: 0,5 кгс/см², 1 кгс/см² и 1,5 кгс/см².

Уравнения для расчета скорости потока жидкости:

Разность давлений;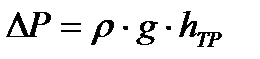

Потери напора в трубопроводе: ;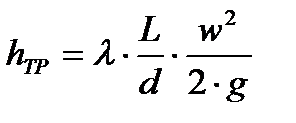

Коэффициент трения: ;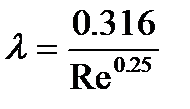

Число Рейнольдса: .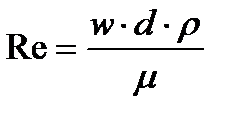

где Δp–разница давлений в емкостях; l – длина трубопровода (l = 100 м), d – внутренний диаметр трубопровода (d= 0.05 м), µ – вязкость жидкости (µ = 10^-3Па·с); ρ – плотность жидкости (ρ = 1000 кг/м³), g – ускорение свободного падения (g = 9.81 м/с²).

Задание 3.

Требуется построить на одном графике несколько зависимостей температур кипения жидкости от давления для смеси метанол-вода при различных концентрациях.

Таблица 4.1.

Концентрации метанола (х₁) и воды (х₂), мол.доля

№ смеси	х1	х2
	0,1	0,9
	0,4	0,6
	0,8	0,2

Уравнения для расчета температуры кипения смеси заданного состава:

.

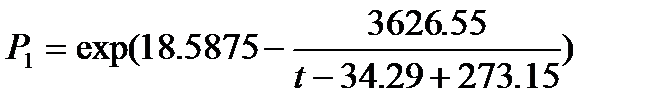
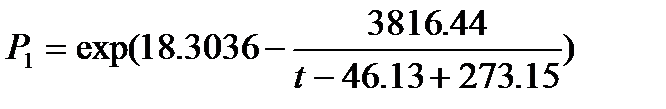
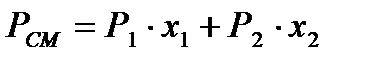где t– температура, ⁰С; Р₁ и Р₂ – давления рассчитанные по уравнению Антуана, для метанола и воды, мм.рт.ст.; Р_СМ – давление, при котором смесь закипит, если имеет температуру t.

Для выполнения данного задания рекомендуется Р_СМ задать как функцию не только температуры, но и составов х₁ и х₂. В этом случае все зависимости будут строится по одной функции, только при постановке их форму графика вместо х₁ и х₂потребуется задать конкретные величины концентраций.

Задание 4.

1. Различие аналитического и численного способов решения уравнений.

2. Как преобразовать задачу поиска значения неизвестной переменной в задачу нахождения корня.

3. Стандартная функция root() и ее аргументы.

4. Как отделить и оценить корни уравнения при помощи графика.

5. Использование функции root() в составе других функций.

Лабораторная работа №4.1.