Уравнения, неравенства и их системы
Линейные уравнения
Квадратные уравнения
Рациональные уравнения
Системы уравнений
Системы неравенств
Линейные уравнения
1.Найдите корни уравнения 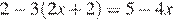 .
.
Решение.
Последовательно получаем:
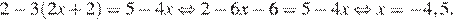
Ответ: −4,5.
Ответ: -4,5
-4,5
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1305.
Задание 6 № 311469
2.Решите уравнение 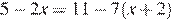 .
.
Решение.
Последовательно получаем:
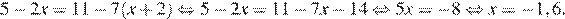
Ответ: −1,6.
Ответ: -1,6
-1,6
Источник: Демоверсия--2012. Математика.
Задание 6 № 338480
3.Решите уравнение 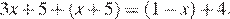
Решение.
Последовательно получаем:
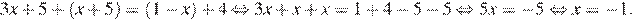
Ответ: −1.
Ответ: -1
-1
Задание 6 № 338488
4.Решите уравнение 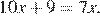
Решение.
Решим уравнение:
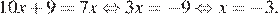
Ответ: −3.
Ответ: -3
-3
Задание 6 № 338495
5.Решите уравнение 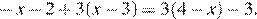
Решение.
Последовательно получаем:
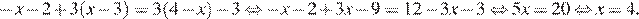
Ответ: 4.
Ответ: 4
Задание 6 № 338500
6.При каком значении  значения выражений
значения выражений 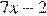 и
и 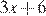 равны?
равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение 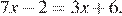 Решим его:
Решим его:
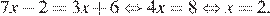
Ответ: 2.
Ответ: 2
Задание 6 № 338509
7.Решите уравнение 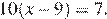
Решение.
Последовательно получаем:

Ответ: 9,7.
Ответ: 9,7
9,7
Задание 6 № 338527
8.Решите уравнение 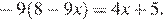
Решение.
Последовательно получаем:
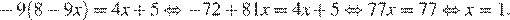
Ответ: 1.
Ответ: 1
Задание 6 № 338557
9.Решите уравнение 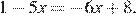
Решение.
Последовательно получаем:
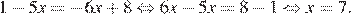
Ответ: 7.
Ответ: 7
Задание 6 № 338560
10.Решите уравнение 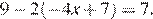
Решение.
Последовательно получаем:
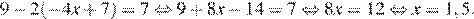
Ответ: 1,5.
Ответ: 1,5
1,5
Задание 6 № 338606
11.Решите уравнение 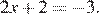
Решение.
Последовательно получаем:
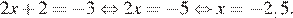
Ответ: −2,5.
Ответ: -2,5
-2,5
Задание 6 № 338610
12.Решите уравнение 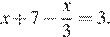
Решение.
Последовательно получаем:
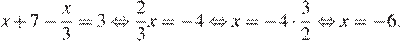
Ответ: -6
-6
Задание 6 № 338658
13.Решите уравнение 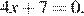
Решение.
Решим уравнение:
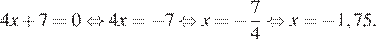
Ответ: −1,75.
Ответ: -1,75
-1,75
Задание 6 № 338868
14.Решите уравнение 
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
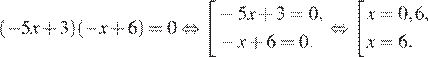
Ответ: 0,66.
Ответ: 0,66
0,66
Источник: Банк заданий ФИПИ
Задание 6 № 341216
15.Решите уравнение 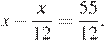
Решение.
Домножим правую и левую часть уравнений на 12:
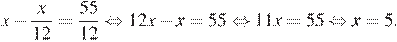
Ответ: 5.
Ответ: 5
Источник: Банк заданий ФИПИ
Задание 6 № 353480
16.Найдите корень уравнения 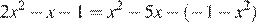
Квадратные уравнения
1.Найдите корни уравнения 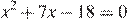 .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
По теореме, обратной теореме Виета, сумма корней равна −7, а их произведение равно −18. Тем самым, это числа −9 и 2.
Ответ: −92.
------------------
Дублирует 314539.
Ответ: -92
-92
Источник: Демонстрационная версия ГИА—2013 по математике.
Задание 6 № 137381
2.Решите уравнение 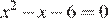 .
.
Решение.
По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение −6.
Тем самым, это числа −2 и 3.
Ответ: −23.
Ответ: -23
-23
Задание 6 № 137382
3.Решите уравнение  .
.
Решение.
Запишем уравнение в виде 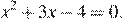 По теореме, обратной теореме Виета, сумма корней равна −3, а их произведение −4.
По теореме, обратной теореме Виета, сумма корней равна −3, а их произведение −4.
Тем самым это числа −4 и 1.
Ответ: −41.
Ответ: -41
-41
Задание 6 № 137383
4.Решите уравнение 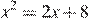 .
.
Решение.
Запишем уравнение в виде 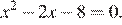 По теореме, обратной теореме Виета, сумма корней равна 2, а их произведение −8.
По теореме, обратной теореме Виета, сумма корней равна 2, а их произведение −8.
Тем самым это числа −2 и 4.
Ответ: −24.
Ответ: -24
-24
Задание 6 № 311405
5.Найдите корни уравнения 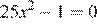 .
.
Решение.
Решим уравнение:
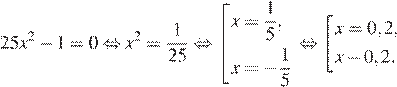
Ответ: −0,20,2.
Ответ: -0,20,2
-0,20,2
Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)
Задание 6 № 311446
6.Найдите корни уравнения 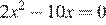 .
.
Решение.
Последовательно получаем:
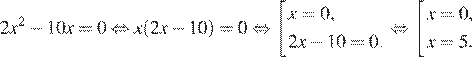
Ответ: 05.
Ответ: 05
Источник: ГИА-2013. Математика. Экзамен. Вариант 9
Задание 6 № 311689
7.Найдите корни уравнения 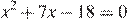
Решение.
По теореме, обратной теореме Виета — сумма корней равна −7, а их произведение равно −18
Тем самым, это числа −9 и 2.
Ответ: −92.
Ответ: -92
-92
Источник: Демонстрационная версия ГИА—2014 по математике.
Задание 6 № 314495
8.Найдите корни уравнения 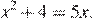
Решение.
Запишем уравнение в виде:
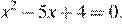
По теореме Виета, сумма корней равна 5, а их произведение равно 4. Тем самым, это числа 4 и 1.
Ответ: 14.
Ответ: 14
Источник: Банк заданий ФИПИ
Задание 6 № 320540
9.  Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Решение.
Уравнения прямых:
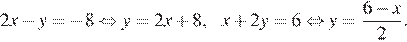
Найдём абсциссу точки пересечения прямых, для этого, приравняем ординаты:
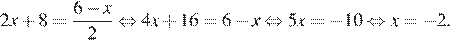
Ответ: −2.
Ответ: -2
-2
Задание 6 № 320541
10.  На рисунке изображены графики функций
На рисунке изображены графики функций 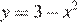 и
и 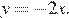 Вычислите координаты точки B.
Вычислите координаты точки B.
Запишите координаты в ответ без пробелов.
Решение.
Точки A и B — точки пересечения графиков функций 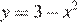 и
и 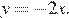 Найдём их абсциссы:
Найдём их абсциссы:
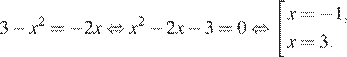
Абсцисса точки B больше нуля, следовательно, это 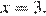 Найдём ординату точки B:
Найдём ординату точки B: 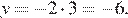
Ответ: 3−6.
Ответ: 3-6
3-6
Задание 6 № 338180
11.Уравнение 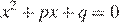 имеет корни −6; 4. Найдите
имеет корни −6; 4. Найдите 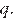
Решение.
По теореме Виета 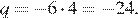
Ответ: −24.
Ответ: -24
-24
Задание 6 № 338202
12.Квадратный трёхчлен разложен на множители: 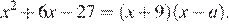 Найдите
Найдите 
Решение.
Корни уравнения 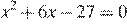 — суть числа −9 и 3. В силу формулы
— суть числа −9 и 3. В силу формулы 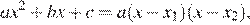 где
где  и
и 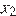 — корни уравнения
— корни уравнения 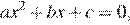 получаем
получаем 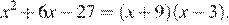 Следовательно,
Следовательно, 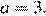
Ответ: 3
Задание 6 № 338494
13.Решите уравнение 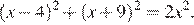
Решение.
Последовательно получаем:
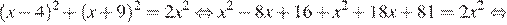
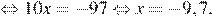
Ответ: −9,7.
Ответ: -9,7
-9,7
Задание 6 № 338518
14.Решите уравнение 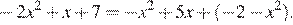
Решение.
Раскроем скобки и преобразуем выражение:
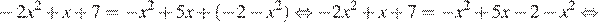
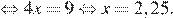
Ответ: 2,25.
Ответ: 2,25
2,25
Задание 6 № 338526
15.Решите уравнение 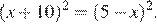
Решение.
Квадраты чисел равны, если числа равны или противоположны:
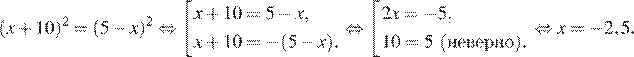
Ответ: −2,5.
Приведем другое решение.
Раскроем скобки в обеих частях уравнения:
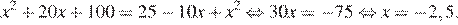
Приведем другое решение.
Воспользуемся формулой разности квадратов:
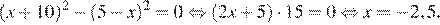
Ответ: -2,5
-2,5
Задание 6 № 338915
16.Решите уравнение 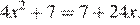
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Последовательно получаем:
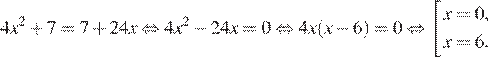
Ответ: 06.
Ответ: 06
Задание 6 № 353508
17.Уравнение 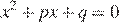 имеет корни −5; 7. Найдите
имеет корни −5; 7. Найдите 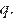
Рациональные уравнения
1.Решите уравнение: 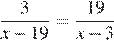 .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Используем свойство пропорции.
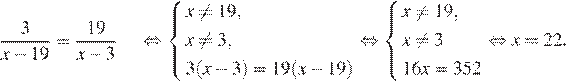
Ответ: 22.
Ответ: 22
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
Задание 6 № 311755
2.Решите уравнение 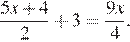
Решение.
Умножим левую и правую часть уравнения на 4, получаем:
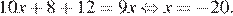
Ответ: −20.
Ответ: -20
-20
Источник: МИОО: Диагностическая работа по математике 01.10.2013 вариант МА90101.
Задание 6 № 316225
3.Решите уравнение: 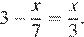
Решение.
Последовательно получаем:
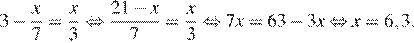
Ответ: 6,3.
Ответ: 6,3
6,3
Источник: Диагностическая работа 01.10.2013 Вариант МА90105
Задание 6 № 316341
4.Решите уравнение: 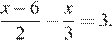
Решение.
Последовательно получаем:
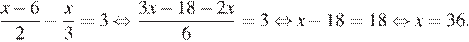
Ответ: 36.
Ответ: 36
Источник: МИОО: Тренировочная работа по математике 19.02.2014 вариант МА90501.
Задание 6 № 338483
5.Решите уравнение 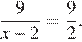
Решение.
Используем свойство пропорции:
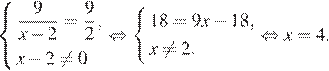
Ответ: 4.
Ответ: 4
Задание 6 № 338503
6.Решите уравнение 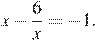
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Умножим обе части уравнения на 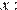
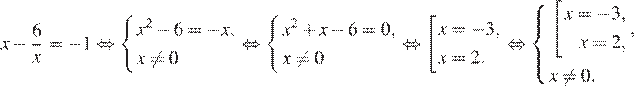
Ответ: −32.
Ответ: -32
-32
Задание 6 № 338583
7.Решите уравнение 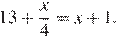
Решение.
Последовательно получаем:
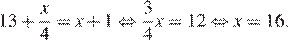
Ответ: 16.
Ответ: 16
Задание 6 № 338723
8.Решите уравнение 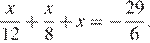
Решение.
Умножим обе части уравнения на 24:
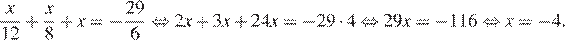
Ответ: −4.
Ответ: -4
-4
Задание 6 № 338805
9.Решите уравнение 
Решение.
Последовательно получаем:
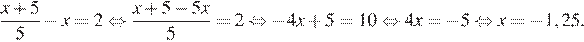
Ответ: −1,25.
Ответ: -1,25
-1,25
Задание 6 № 338937
10.Решите уравнение 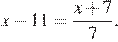
Решение.
Умножим обе части уравнения на 7:
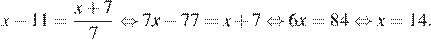
Ответ: 14.
Ответ: 14
Задание 6 № 341402
11.Решите уравнение 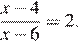
Системы уравнений
1.Решите систему уравнений 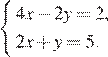
В ответе запишите сумму решений системы.
Решение.
Разделим обе части первого уравнения на 2 и решим систему методом подстановки:
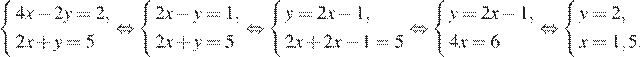
Ответ: 3,5.
Примечание.
Систему можно было бы решить методом алгебраического сложения:
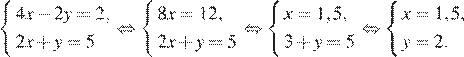
Ответ: 3,5
3,5
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 1)
Задание 6 № 311327
2.Решите систему уравнений 
В ответе запишите сумму решений системы.
Решение.
Решим систему методом подстановки:
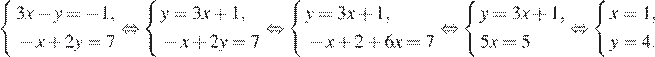
Ответ: 5.
Ответ: 5
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)
Задание 6 № 311338
3.Решите систему уравнений 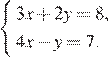
В ответе запишите сумму решений системы.
Решение.
Решим систему методом подстановки:
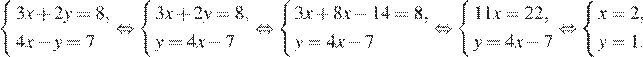
Ответ: 3.
Ответ: 3
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 3)
Задание 6 № 311350
4.Решите систему уравнений 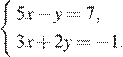
В ответе запишите сумму решений системы.
Решение.
Решим систему методом подстановки:
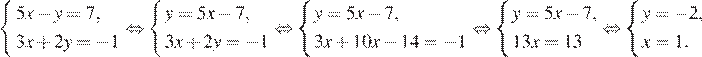
Ответ: −1.
Ответ: -1
-1
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
Задание 6 № 311360
5.Решите систему уравнений 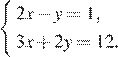
В ответе запишите сумму решений системы.
Решение.
Решим систему методом подстановки:
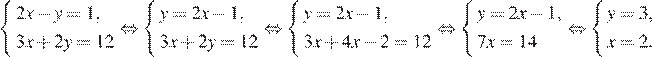
Ответ: 5.
Ответ: 5
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.5)
Задание 6 № 311370
6.Решите систему уравнений 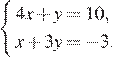
В ответе запишите сумму решений системы.
Системы неравенств
1.Найдите наибольшее значение x, удовлетворяющее системе неравенств 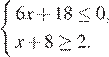
Решение.
Решим систему:
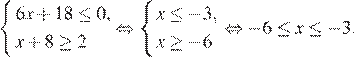
Искомое наибольшее решение равно −3.
Ответ: −3.
Ответ: -3
-3
Источник: Банк заданий ФИПИ
Задание 6 № 314543
2.Найдите наибольшее значение  , удовлетворяющее системе неравенств
, удовлетворяющее системе неравенств 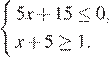
Графики функции
Чтение графиков
Растяжение и сдвиги
Чтение графиков
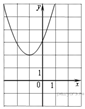
1.Найдите значение  по графику функции
по графику функции 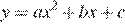 , изображенному на рисунке.
, изображенному на рисунке.
1) 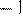 2)
2) 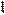 3)
3) 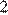 4)
4) 
Решение.
Абсцисса вершины параболы равна −1, поэтому 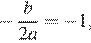 откуда
откуда 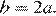 Парабола пересекает ось ординат в точке с ординатой 3, поэтому
Парабола пересекает ось ординат в точке с ординатой 3, поэтому 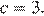 Тем самым, уравнение параболы принимает вид
Тем самым, уравнение параболы принимает вид 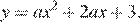 Поскольку парабола проходит через точку (−1; 2), имеем:
Поскольку парабола проходит через точку (−1; 2), имеем:
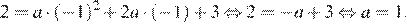
Верный ответ указан под номером 2.
Ответ: 2.
Ответ: 2
Задание 10 № 193090
2.Найдите значение  по графику функции
по графику функции 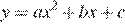 , изображенному на рисунке.
, изображенному на рисунке.
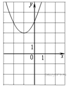
1) 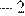 2)
2) 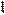 3)
3) 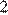 4)
4) 
Решение.
Абсцисса вершины параболы равна −1, поэтому 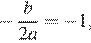 откуда
откуда 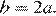 Парабола пересекает ось ординат в точке с ординатой 3, поэтому
Парабола пересекает ось ординат в точке с ординатой 3, поэтому 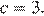 Тем самым, уравнение параболы принимает вид
Тем самым, уравнение параболы принимает вид 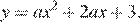 Поскольку парабола проходит через точку (−1; 2), имеем:
Поскольку парабола проходит через точку (−1; 2), имеем:
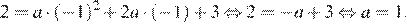
Таким образом,
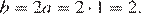
Верный ответ указан под номером 3.
Ответ: 3.
Ответ: 3
Задание 10 № 193091
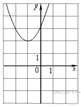
3.Найдите значение  по графику функции
по графику функции 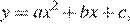 изображенному на рисунке.
изображенному на рисунке.
1) 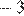 2)
2) 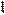 3)
3) 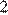 4)
4) 
Решение.
Значение  — это значение графика при ордината графика при
— это значение графика при ордината графика при 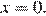 Значит,
Значит, 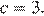 Такой ответ указан под номером 4.
Такой ответ указан под номером 4.
Ответ: 4.
Ответ: 4
Задание 10 № 193102
4.Найдите значение 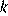 по графику функции
по графику функции  изображенному на рисунке.
изображенному на рисунке.
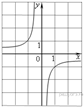
Решение.
Поскольку гипербола проходит через точку (−1; 1), имеем: 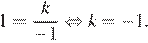
Ответ: −1.
Ответ: -1
-1
Задание 10 № 311406
5.На рисунке изображён график функции 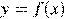 . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.
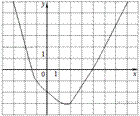
1) функция возрастает на промежутке 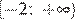
2) 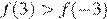 3)
3) 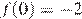
4) прямая  пересекает график в точках
пересекает график в точках 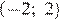 и
и 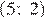
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке 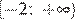 — неверно, функция убывает на промежутке
— неверно, функция убывает на промежутке 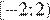 и затем возрастает на
и затем возрастает на 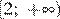 .
.
2) 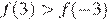 — неверно,
— неверно, 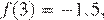
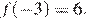
3) 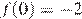 — верно, видно из графика.
— верно, видно из графика.
4) Прямая  пересекает график в точках
пересекает график в точках 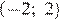 и
и 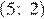 — верно, видно из графика.
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
Ответ: 12|21
12|21
Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)
Задание 10 № 314676
6. 
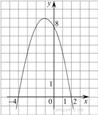
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания.
1) Функция возрастает на промежутке (−∞; −1].
2) Наибольшее значение функции равно 8.
3) f(−4) ≠ f(2).
Решение.
Проверим каждое утверждение.
1) На луче (−∞; −1] большему значению аргумента сответствует большее значение функции. Следовательно, функция возрастает на этом луче; первое утверждение верно.
2) Наибольшее значение функции равно 9. Второе утверждение неверно.
3) Значения фунцкии в точках −4 и 2 равны нулю, поэтому f(−4) = f(2). Третье утверждение неверно.
Ответ: 23.
Ответ: 23
Источник: Банк заданий ФИПИ
Задание 10 № 314703
7. 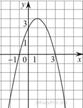
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(−1) = f(3).
2) Наибольшее значение функции равно 3.
3) f(x)>0 при −1<x<3.
Решение.
Проверим каждое утверждение.
1) f(−1) = f(3). Первое утверждение верно.
2) Наибольшее значение функции равно 4. Второе утверждение неверно.
3) f(x)>0 при −1<x<3. Третье утверждение верно.
Ответ: 2.
Ответ: 2
Источник: Банк заданий ФИПИ
Задание 10 № 314704
8. 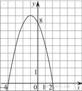
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наибольшее значение функции равно 9.
2) f(0)>f(1).
3) f( x )>0 при x<0.
Решение.
Проверим каждое утверждение.
1) Наибольшее значение функции равно 9. Первое утверждение верно.
2) Значения фунцкии в точке 0 равно 8, а в точке 1 — 5 поэтому f(0) > f(1). Второе утверждение верно.
3) На луче (−∞; 0) функция принимает как положительные так и отрицательные значения. Третье утверждение неверно.
Ответ: 3.
Ответ: 3
Источник: Банк заданий ФИПИ
Задание 10 № 333008
9.На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
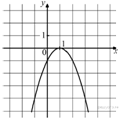
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | 1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3] |
Ответ: 
Решение.
Функция, изображённая на графике возрастает на промежутке 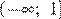 и убывает на промежутке
и убывает на промежутке 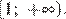 Следовательно, на данных промежутках функция возрастает на третьем промежутке и убывает на первом.
Следовательно, на данных промежутках функция возрастает на третьем промежутке и убывает на первом.
Ответ: 31.
Ответ: 31
Источник: МИОО: Диагностическая работа по математике 17.04.2014 вариант МА90601
Задание 10 № 333087
10.На рисунке изображён график функции вида 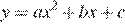 . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
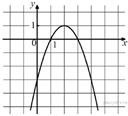
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | 1) [0; 3] 2) [−1; 1] 3) [2; 4] 4) [1; 4] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б |
Решение.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Данная функция возрастает на промежутке 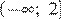 и убывает на промежутке
и убывает на промежутке 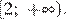 Таким образом, из приведённых промежутков функция только возрастает на промежутке
Таким образом, из приведённых промежутков функция только возрастает на промежутке 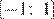 убывает на промежутке
убывает на промежутке 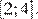
Ответ: 23.
Ответ: 23
Источник: МИОО: Диагностическая работа по математике 17.04.2014 вариант МА90602
Задание 10 № 339184
11.На рисунке изображены графики функций вида y = ax2 + bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D.
А)  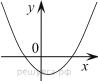 | Б)  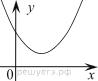 | В)  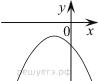 | Г)  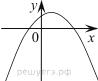 |
| 1) a > 0, D > 0 | 2) a > 0, D < 0 | 3) a < 0, D > 0 | 4) a < 0, D < 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Растяжение и сдвиги
1.Установите соответствие между графиками функций и формулами, которые их задают.
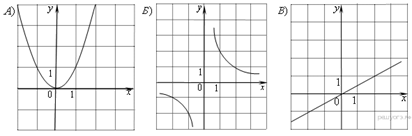
1) 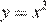 2)
2) 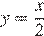 3)
3) 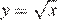 4)
4) 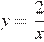
| А | Б | В |
Решение.
Определим вид графика каждой из функций.
1) 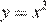 — уравнение параболы, ветви которой направленны вверх.
— уравнение параболы, ветви которой направленны вверх.
2) 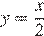 — уравнение прямой.
— уравнение прямой.
3) 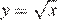 — уравнение верхней ветви параболы, направленной вправо.
— уравнение верхней ветви параболы, направленной вправо.
4) 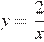 — уравнение гиперболы.
— уравнение гиперболы.
Тем самым найдено соответствие: A — 1, Б — 4, В — 2.
Ответ: 142.
Ответ: 142
Источник: Демонстрационная версия ГИА—2013 по математике.
Задание 10 № 193087
2.График какой из приведенных ниже функций изображен на рисунке?
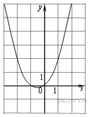
1) 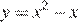 | 2) 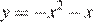 | 3) 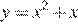 | 4) 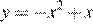 |
Решение.
Ветви изображённой на рисунке параболы направленны вверх, а абсцисса вершины отрицательна. Следовательно, данному графику могут соответсвовать функции 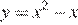 или
или 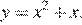 Выделим полный квадрат в обоих выражениях:
Выделим полный квадрат в обоих выражениях:
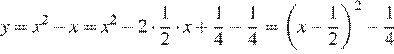
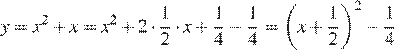
Графику соответствует вариант под номером 3.
Ответ: 3
Задание 10 № 193093
3.На одном из рисунков изображен график функции 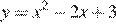 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
| 1) | 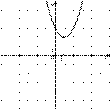 | 2) | 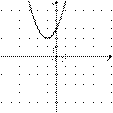 |
| 3) | 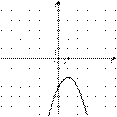 | 4) | 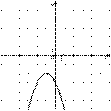 |
Решение.
Коэффициент 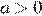 , поэтому ветви параболы направлены вверх. Абсцисса вершины параболы равна:
, поэтому ветви параболы направлены вверх. Абсцисса вершины параболы равна: 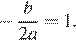
Правильный вариант ответа указан под номером 1.
Ответ: 1
Задание 10 № 193097
4.На одном из рисунков изображена парабола. Укажите номер этого рисунка.
| 1) | 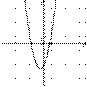 | 2) | 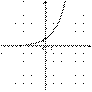 |
| 3) | 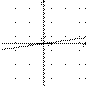 | 4) | 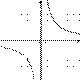 |
Решение.
Парабола изображена на рисунке 1.
Правильный ответ указан под номером 1.
Ответ: 1
Задание 10 № 198175
5.График какой из приведенных ниже функций изображен на рисунке?
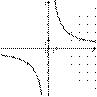
1)  | 2) 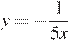 | 3) 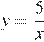 | 4) 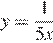 |
Решение.
Изображённая на рисунке гипербола расположена в первой и третьей четвертях, следовательно, данному графику могут соответсвовать функции 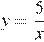 или
или 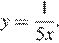 При
При 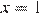 ордината функции на графике равна 5, следовательно, это график функции
ордината функции на графике равна 5, следовательно, это график функции 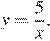
Ответ: 3.
Ответ: 3
Задание 10 № 200515
6.На одном из рисунков изображен график функции 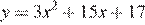 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
| 1) | 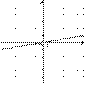 | 2) | 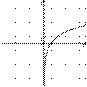 |
| 3) | 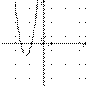 | 4) | 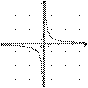 |
Решение.
График функции 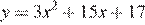 — парабола. Определим тип каждого графика функции.
— парабола. Определим тип каждого графика функции.
1) На первом рисунке изображена линейная функция.
2) На втором рисунке изображена логарифмическая функция.
3) На третьем р<
