Линейные неравенства. Системы линейных неравенств

Уравнение – хорошо, в жизни пригодится, но не менее важно знать геометрический смысл линейных неравенств двух переменных. Принципиальное отличие от неравенств с одной переменной состоит в размерности.

Линейные неравенства

Различают два типа линейных неравенств:

1) Строгие неравенства: .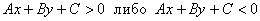

2) Нестрогие неравенства: .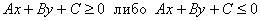

Какой геометрический смысл этих неравенств? Если линейное уравнение 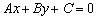задаёт прямую, то линейное неравенство определяет полуплоскость.

Для понимания нижеследующей информации нужно знать разновидности прямых на плоскости и уметь строить прямые. Начнём с простейших линейных неравенств.

Как известно, ось абсцисс 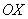задаётся уравнением 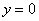– «игрек» всегда (при любом значении «икс») равняется нулю

Рассмотрим неравенство 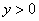. Как его понимать неформально? «Игрек» всегда (при любом значении «икс») положителен. Очевидно, что данное неравенство определяет верхнюю полуплоскость – ведь там и находятся все точки с положительными «игреками».

В том случае, если неравенство нестрогое 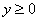, к верхней полуплоскости дополнительно добавляется сама ось .

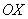Аналогично: неравенству 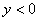удовлетворяют все точки нижней полуплоскости, нестрогому неравенству 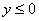соответствует нижняя полуплоскость + ось .

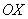С осью ординат 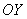та же самая прозаичная история:

– неравенство 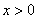задаёт правую полуплоскость;
– неравенство 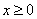задаёт правую полуплоскость, включая ось ординат;
– неравенство задаёт левую полуплоскость;
– неравенство 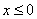задаёт левую полуплоскость, включая ось ординат.

На втором шаге рассмотрим неравенства, в которых отсутствует одна из переменных.

Отсутствует «игрек»:

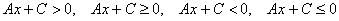
Или отсутствует «икс»:

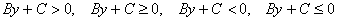
С такими неравенствами можно разобраться двумя способами, пожалуйста, рассмотрите оба подхода.

Пример 1

Решить линейные неравенства:

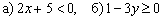
Что значит решить линейное неравенство?

Решить линейное неравенство – это значит найти полуплоскость, точки которой удовлетворяют данному неравенству (плюс саму прямую, если неравенство нестрогое).Решение, как правило, графическое.

Удобнее сразу выполнить чертёж, а потом всё закомментировать:

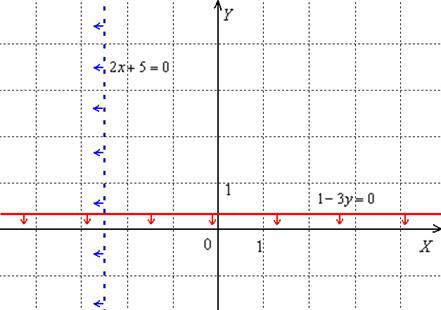
а) Решим неравенство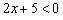

Способ первый

Способ весьма напоминает историю с координатными осями, которую мы рассмотрели выше. Идея состоит в преобразовании неравенства – чтобы в левой части оставить одну переменную без всяких констант, в данном случае – переменную «икс».

Правило: В неравенстве слагаемые переносятся из части в часть со сменой знака, при этом знак САМОГО неравенства не меняется (например, если был знак «меньше», то так и останется «меньше»).

Переносим «пятёрку» в правую часть со сменой знака:

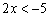
Правило: Обе части неравенства можно умножить (разделить) на ПОЛОЖИТЕЛЬНОЕ число, при этом знак неравенства не меняется.

Умножаем обе части неравенства на :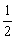

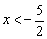
Теперь чертим прямую 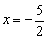(синяя пунктирная линия). Прямая проведена пунктиром по той причине, что неравенство строгое, и точки, принадлежащие данной прямой, заведомо не будут входить в решение.

Каков смысл неравенства 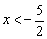? «Икс» всегда (при любом значении «игрек») меньше, чем 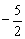. Очевидно, что этому утверждению удовлетворяют все точки левой полуплоскости. Данную полуплоскость, в принципе, можно заштриховать, но я ограничусь маленькими синими стрелочками.

Способ второй

Это универсальный способ. ЧИТАЕМ ОЧЕНЬ ВНИМАТЕЛЬНО!

Сначала чертим прямую 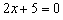. Для ясности, кстати, уравнение целесообразно представить в виде .

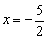Теперь выбираем любую точку плоскости, не принадлежащую прямой. В большинстве случаев, самая лакомая точка, конечно 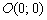. Подставим координаты данной точки в неравенство :

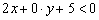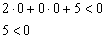
Получено неверное неравенство (простыми словами, так быть не может), значит, точка 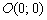не удовлетворяет неравенству .

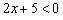Ключевое правило нашей задачи:
– Если какая-либо точка полуплоскости (не принадлежащая прямой) не удовлетворяет неравенству, то и ВСЕ точки данной полуплоскости не удовлетворяют данному неравенству.
– Если какая-либо точка полуплоскости (не принадлежащая прямой) удовлетворяет неравенству, то и ВСЕ точки данной полуплоскости удовлетворяют данному неравенству.

Можете протестировать: любая точка справа от прямой 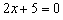не будет удовлетворять неравенству .

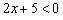Какой вывод из проведённого опыта с точкой 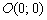? Деваться некуда, неравенству 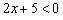удовлетворяют все точки другой – левой полуплоскости (тоже можете проверить).

б) Решим неравенство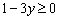

Способ первый

Преобразуем неравенство:

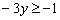
Правило: Обе части неравенства можно умножить (разделить) на ОТРИЦАТЕЛЬНОЕ число, при этом знак неравенства МЕНЯЕТСЯ на противоположный (например, если был знак «больше либо равно», то станет «меньше либо равно»).

Умножаем обе части неравенства на :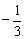

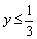
Начертим прямую 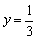(красный цвет), причём, начертим сплошной линией, так как неравенство у нас нестрогое, и прямая заведомо принадлежит решению.

Проанализировав полученное неравенство 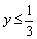, приходим к выводу, что его решением является нижняя полуплоскость (+ сама прямая).

Подходящую полуплоскость штрихуем либо помечаем стрелочками.

Способ второй

Начертим прямую 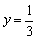. Выберем произвольную точку плоскости (не принадлежащую прямой), например, 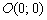и подставим её координаты в наше неравенство :

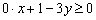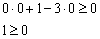
Получено верное неравенство, значит, точка 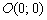удовлетворяет неравенству 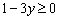, и вообще – ВСЕ точки нижней полуплоскости удовлетворяют данному неравенству.

Здесь подопытной точкой мы «попали» в нужную полуплоскость.

Решение задачи обозначено красной прямой и красными стрелочками.

Пример 2

Решить линейные неравенства:

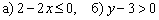
Это пример для самостоятельного решения. Постарайтесь решить задачу двумя способами (к слову, это хороший способ проверки решения). В ответе в конце урока будет только итоговый чертёж.

Переходим к рассмотрению третьего, общего случая, когда в неравенстве присутствуют обе переменные:

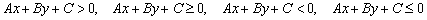
Как вариант, свободный член «ц» может быть нулевым.

Пример 3

Найти полуплоскости, соответствующие следующим неравенствам:

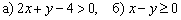
Решение: Здесь используется универсальный метод решения с подстановкой точки.

а) Построим уравнение прямой 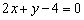, при этом линию следует провести пунктиром, так как неравенство строгое и сама прямая не войдёт в решение.

Выбираем подопытную точку плоскости, которая не принадлежит данной прямой, например, 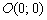, и подставим её координаты в наше неравенство:

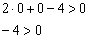
Получено неверное неравенство, значит, точка 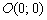и ВСЕ точки данной полуплоскости не удовлетворяют неравенству 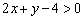. Решением неравенства будет другая полуплоскость, любуемся синими молниями:

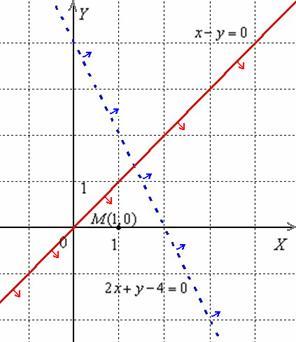
б) Решим неравенство 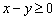. Сначала построим прямую. Это сделать несложно, перед нами каноничная прямая пропорциональность 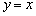. Линию проводим сплошняком, так как неравенство нестрогое.

Выберем произвольную точку плоскости, не принадлежащую прямой 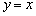. Хотелось бы снова использовать начало координат, но, увы, сейчас оно не годится. Выгоднее взять точку с небольшими значениями координат, например, 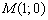. Подставим её координаты в наше неравенство:

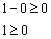
Получено верное неравенство, значит, точка 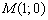и все точки данной полуплоскости удовлетворяют неравенству 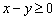. Искомая полуплоскость помечена красными стрелочками. Кроме того, в решение входит сама прямая .

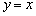Пример 4

Найти полуплоскости, соответствующие неравенствам:

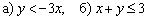
Это пример для самостоятельного решения. Полное решение, примерный образец чистового оформления и ответ в конце.

Разберём обратную задачу:

Пример 5

а) Дана прямая 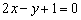. Составить уравнение полуплоскости, в которой находится точка 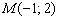, при этом сама прямая должна входить в решение.

б) Дана прямая 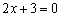. Составить уравнение полуплоскости, в которой находится точка 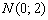. Сама прямая не входит в решение.

Решение: здесь нет необходимости в чертеже, и решение будет аналитическим. Ничего трудного:

а) Составим вспомогательный многочлен 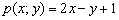и вычислим его значение в точке :
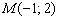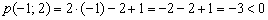. Таким образом, искомое неравенство будет со знаком «меньше». По условию прямая 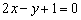входит в решение, поэтому неравенство будет нестрогим: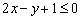

б) Составим многочлен 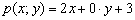и вычислим его значение в точке :
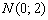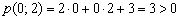. Таким образом, искомое неравенство будет со знаком «больше». По условию прямая 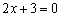не входит в решение, следовательно, неравенство будет строгим: .

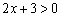Ответ: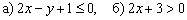

Творческий пример для самостоятельного изучения:

Пример 6

Даны точки 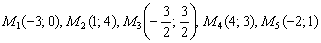и прямая 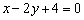. Среди перечисленных точек найти те, которые вместе с началом координат лежат по одну сторону от заданной прямой.

Небольшая подсказка: сначала нужно составить неравенство, определяющее полуплоскость, в которой находится начало координат. Аналитическое решение и ответ в конце

Системы линейных неравенств

Что значит решить систему линейных неравенств?

Решить систему линейных неравенств – это значит найти множество точек плоскости, которые удовлетворяют каждому неравенству системы.

В качестве простейших примеров рассмотрим системы неравенств, определяющих координатные четверти прямоугольной системы координат

Система неравенств 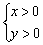задаёт первую координатную четверть (правая верхняя). Координаты любой точки первой четверти, например, 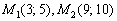и т.д. удовлетворяют каждому неравенству данной системы.

Аналогично:
– система неравенств 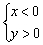задаёт вторую координатную четверть (левая верхняя);
– система неравенств 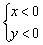задаёт третью координатную четверть (левая нижняя);
– система неравенств 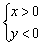задаёт четвёртую координатную четверть (правая нижняя).

Система линейных неравенств может не иметь решений, то есть, быть несовместной. Снова простейший пример: 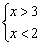. Совершенно очевидно, что «икс» не может одновременно быть больше трёх и меньше двух.

Решением системы неравенств может являться прямая, например: 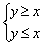решением данной системы является прямая .

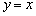Но самый распространённый случай, когда решением системы является некоторая область плоскости. Область решений может быть не ограниченной (например, координатные четверти) либо ограниченной. Ограниченная область решений называется многоугольником решений системы.

Пример 7

Решить систему линейных неравенств

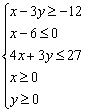
На практике в большинстве случаев приходится иметь дело с нестрогими неравенствами

Решение: то, что неравенств многовато, пугать не должно. Сколько может быть неравенств в системе? Да сколько угодно. Главное, придерживаться рационального алгоритма построения области решений:

1) Сначала разбираемся с простейшими неравенствами. Неравенства 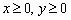определяют первую координатную четверть, включая границу из координатных осей. Уже значительно легче, так как область поиска значительно сузилась. На чертеже сразу отмечаем стрелочками соответствующие полуплоскости (красные и синие стрелки)

2) Второе по простоте неравенство 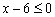– здесь отсутствует «игрек». Во-первых, строим саму прямую 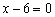, а, во-вторых, после преобразования неравенства к виду 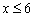, сразу становится понятно, что все «иксы» меньше, чем 6. Отмечаем зелёными стрелками соответствующую полуплоскость. Ну что же, область поиска стала ещё меньше – такой не ограниченный сверху прямоугольник.

3) На последнем шаге решаем неравенства «с полной амуницией»: 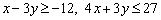. Алгоритм решения мы подробно рассмотрели в предыдущем параграфе. Вкратце: сначала строим прямую, потом с помощью подопытной точки находим нужную нам полуплоскость.

Встаньте, дети, встаньте в круг:

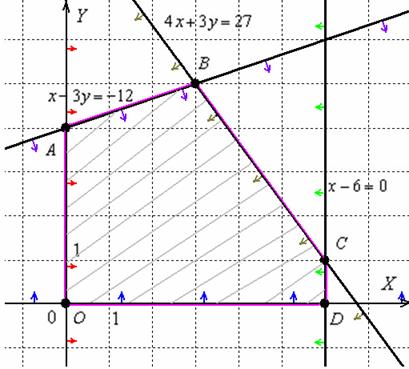
Область решений системы представляет собой многоугольник 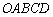, на чертеже он обведён малиновой линией и заштрихован

Любая точка данного многоугольника удовлетворяет КАЖДОМУ неравенству системы (для интереса можете проверить).

Ответ: решением системы является многоугольник .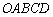

При оформлении на чистовик неплохо бы подробно расписать, по каким точкам вы строили прямые, и как определяли полуплоскости (см. первый параграф данного урока). Однако на практике в большинстве случаев вам зачтут и просто правильный чертёж. Сами же расчёты можно проводить на черновике или даже устно.

Помимо многоугольника решений системы, на практике, пусть и реже, встречается открытая область. Попытайтесь разобрать следующий пример самостоятельно. Хотя, точности ради, пыток тут никаких – алгоритм построения такой же, просто область получится не ограниченной.

Пример 8

Решить систему

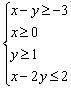
Пример 9

Решить систему и найти координаты вершин полученной области

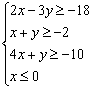
Решение: изобразим на чертеже область решений данной системы. Неравенство 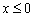задаёт левую полуплоскость с осью ординат, и халявы тут больше нет. После расчётов на чистовике/черновике или глубоких мыслительных процессов, получаем следующую область решений:

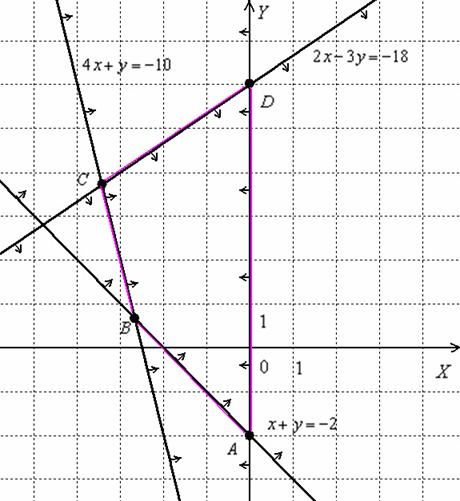
Область решений представляет собой многоугольник 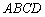. Теперь нужно найти координаты вершин полученной области. Здесь ясно прорисовались координаты только двух точек: 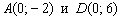. Остаётся решить вопрос с точками .

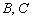Нетрудно заметить, что вершины 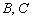являются точками пересечением прямых..

Найдём координаты вершины :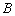

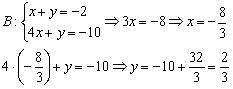
Примечание: из второго уравнения системы почленно вычтено первое уравнение.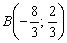

Найдём координаты точки :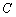

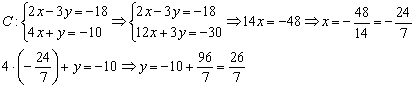
Примечание: второе уравнение системы умножено на 3, затем уравнения сложены почленно.

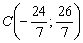
Для красоты координаты точек 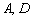тоже можно найти аналитическим методом:

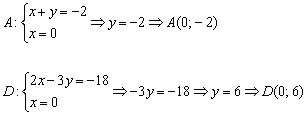
Ответ: область решений системы представляет собой многоугольник с вершинами в точках .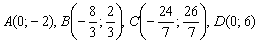

для самостоятельного решения:

Пример 10

Найти область решений системы и координаты вершин полученной области

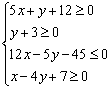
И опять же, буквенные обозначения вершин многоугольника у нас могут отличаться. У меня будет точка «цэ», а у вас эта же вершина может быть обозначена через «дэ».

Мы рассмотрели примеры средней степени сложности, чего вполне достаточно. В ряде задач, например, в задаче линейного программирования коэффициенты неравенств обычно велики, и приходиться возиться (иногда долго) с подбором масштаба и построением самих прямых.

Желаю успехов!

Решения и ответы:

Пример 2: Ответ:

Пример 4: Решение:
а) Построим прямую 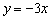. Выберем произвольную точку плоскости, не принадлежащую данной прямой, например, 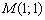и подставим её координаты в неравенство:

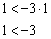
Получено неверное неравенство, значит, неравенство 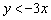задаёт полуплоскость, которой не принадлежит точка 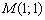, при этом прямая 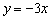не входит в решение.
б) Построим прямую 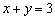. Выберем произвольную точку плоскости, не принадлежащую данной прямой, например, 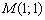и подставим её координаты в неравенство:

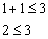
Получено верное неравенство, значит, неравенство 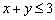задаёт полуплоскость, в которой находится точка 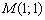, при этом прямая 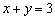входит в решение.
Ответ:

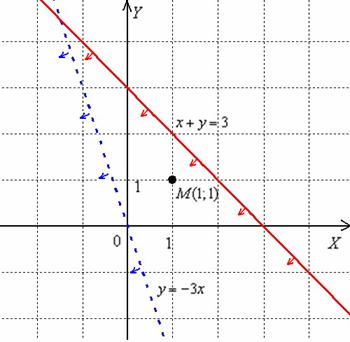
Пример 6: Решение: Составим многочлен 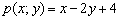и вычислим его значение в точке :
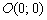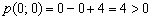, следовательно, искомые точки должны удовлетворять неравенству 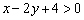(а значит, и условию ).
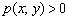Вычислим значения многочлена в каждой из пяти точек:

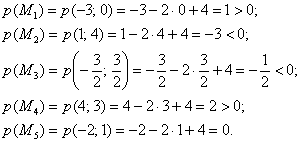
Условию 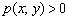удовлетворяют точки .
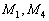Ответ: в одной полуплоскости с началом координат лежат точки .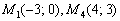

Пример 8: Решение: изобразим на чертеже область решений, соответствующую заданной системе линейных неравенств:

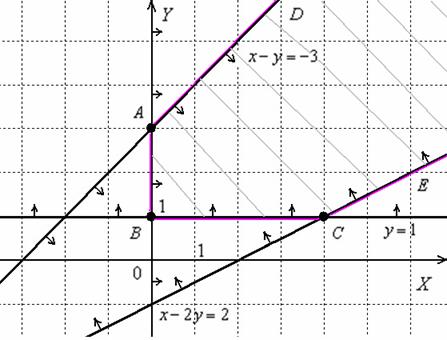
Ответ: область решений системы ограничена ломаной 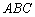и лучами .

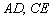Пример 10: Решение: изобразим на чертеже область решений данной системы неравенств:

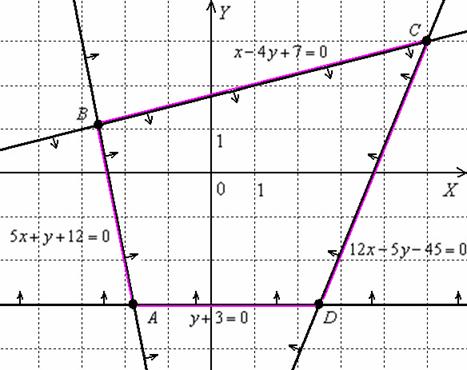
Область решений представляет собой многоугольник 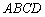. Найдём координаты вершин полученной области:

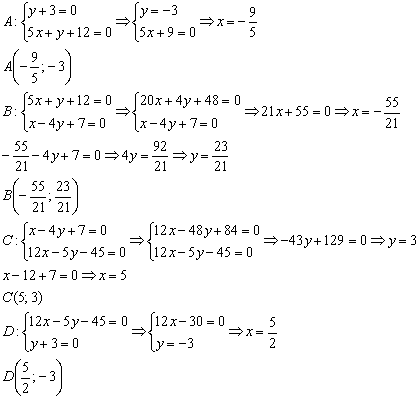
Ответ: область решений системы представляет собой многоугольник с вершинами в точках .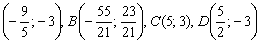

Типовая задача

Пример 1

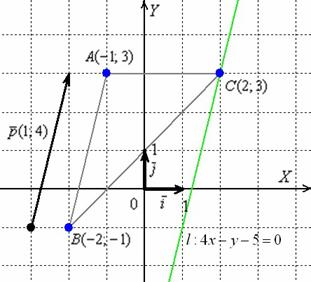
Даны три вершины параллелограмма 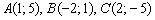. Найти четвёртую вершину .

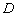Начинаем разбираться:

Шаг первый: очевидно, что речь идёт о «плоской» задаче.

Шаг второй: в задаче речь идёт о параллелограмме.

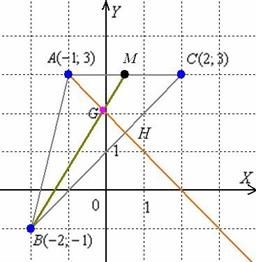
Шаг третий: Выполним чертёж, на котором отметим три известные вершины.

несложно сразу построить искомую точку :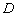

Построить, это, конечно, хорошо, но решение необходимо оформить аналитически.

Шаг четвёртый: Разработка алгоритма решения. Первое, что приходит в голову – точку 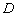можно найти как пересечение прямых 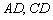. Их уравнения нам неизвестны, поэтому придётся заняться этим вопросом:

1) Противоположные стороны 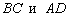параллельны. По точкам 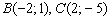найдём направляющий вектор данных сторон .

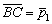2) Составим уравнение прямой 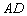по известной точке 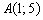и найденному направляющему вектору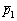

3) Противоположные стороны 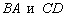параллельны. По точкам 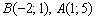найдём направляющий вектор этих сторон .

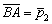4) Составим уравнение прямой 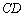по точке 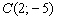и направляющему вектору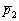

Можно было пойти более длинным путём – сначала найти уравнения прямых 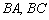и только потом «вытащить» из них направляющие векторы .

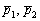5) Теперь уравнения прямых 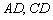известны. Осталось составить и решить соответствующую систему линейных уравнений

Точка 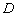найдена.

Задача довольно таки простая и её решение очевидно, но существует более короткий путь!

Второй способ решения:

Диагонали параллелограмма своей точкой пересечения делятся пополам. Точку 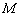я отметил, но чтобы не загромождать чертёж сами диагонали не провёл.

1) С помощью формул координат середины отрезка найдём точку 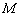– середину диагонали .

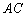2) Рассмотрим диагональ 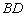. Из условия известна вершина «б», из предыдущего пункта найдена середина 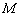. Используя те же формулы координат середины отрезка, находим вершину .

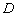Хорошее знание свойств параллелограмма позволило значительно сократить решение!

Переходим к наиболее распространённой задаче, которая встречается практически в каждом сборнике, в каждой методичке:

Типовая задача с треугольником на плоскости

Типовая задача с треугольником на плоскости, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше.

Пример 1

Даны вершины треугольника 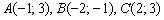. Требуется:

1) составить уравнения сторон 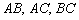и найти их угловые коэффициенты;
2) найти длину стороны ;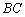
3) найти ;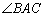
4) составить уравнение прямой 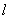, проходящей через точку 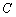параллельно прямой ;
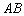5) составить уравнение высоты 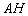и найти её длину;
6) вычислить площадь треугольника ;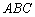
7) составить уравнение медианы ;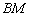
8) найти точку пересечения .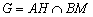

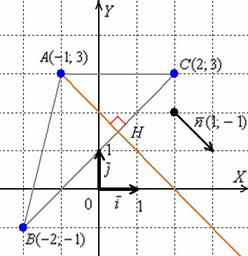
Решение: С чего начать? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и самопроверки всегда строим чертёж на черновике.

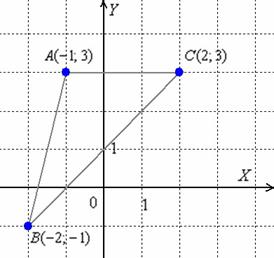
Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1 см (2 тетрадные клетки).

1) Составим уравнения сторон 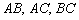и найдём их угловые коэффициенты.

Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум точкам.

Составим уравнение стороны 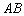по точкам :

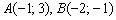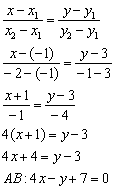
Для проверки следует мысленно либо на черновике подставить координаты каждой точки в полученное уравнение. Теперь найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:

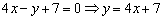
Таким образом, угловой коэффициент: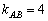

Аналогично находим уравнения сторон 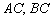. Не вижу особого смысла расписывать то же самое, поэтому сразу приведу готовый результат:

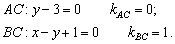
2) Найдём длину стороны 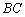. Для точек 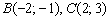используем формулу:

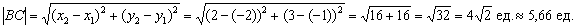
По этой же формуле легко найти и длины других сторон. Проверка очень быстро выполнятся обычной линейкой.

3) Найдём 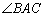. Это угол при вершине 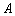. Есть несколько способов решения, но самый универсальный способ – находить угол при вершине, как угол между векторами.

Используем формулу .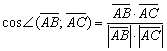

Найдём векторы:

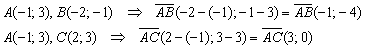
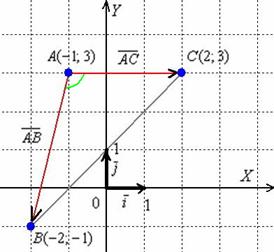
Таким образом:

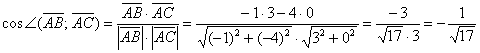
Кстати, попутно мы нашли длины сторон .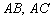

В результате:

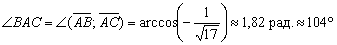
Ну что же, похоже на правду, для убедительности к углу можно приложить транспортир.

Внимание! Не путайте угол треугольника с углом между прямыми. Угол треугольника может быть тупым, а угол между прямыми – нет .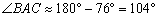

4) Составить уравнение прямой 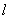, проходящей через точку 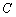параллельно прямой .

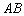Из общего уравнения прямой 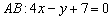вытащим направляющий вектор 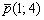. Составим уравнение прямой 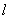по точке 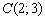и направляющему вектору :

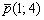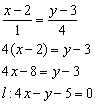
Как найти высоту треугольника?

5) Составим уравнение высоты 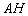и найдём её длину.

Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

То есть, необходимо составить уравнение перпендикуляра, проведённого из вершины 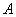к стороне 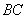. Из уравнения 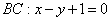снимаем вектор нормали 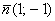. Уравнение высоты 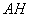составим по точке 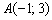и направляющему вектору :

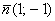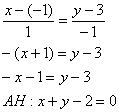
Обратите внимание, что координаты точки 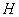нам не известны.

Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: 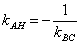. В данном случае 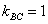, тогда: 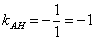. Уравнение высоты 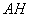составим по точке 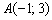и угловому коэффициенту :

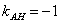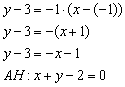
Длину высоты можно найти двумя способами.

Существует окольный путь:

а) находим 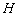– точку пересечения высоты и стороны ;
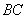б) находим длину отрезка 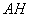по двум известным точкам.

Точка известна: 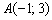, уравнение прямой тоже известно: 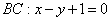, Таким образом:

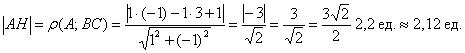
5) Вычислим площадь треугольника. В пространстве площадь треугольника традиционно рассчитывается с помощью векторного произведения векторов, но здесь дан треугольник на плоскости. Используем школьную формулу:
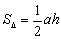– площадь треугольника равна половине произведения его основания на высоту.

В данном случае:

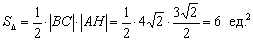
Как найти медиану треугольника?

7) Составим уравнение медианы .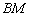

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

а) Найдём точку 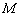– середину стороны 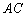. Используем формулы координат середины отрезка. Известны конца отрезка: 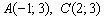, тогда координаты середины:

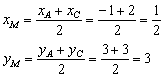
Таким образом: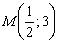

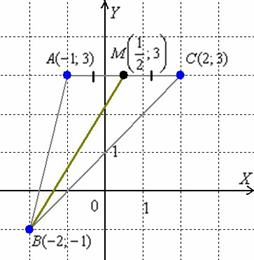
Уравнение медианы 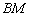составим по точкам :

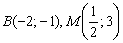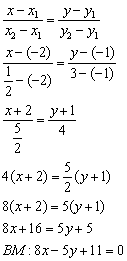
Чтобы проверить уравнение, в него нужно подставить координаты точек .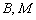

8) Найдём точку пересечения 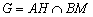высоты и медианы.

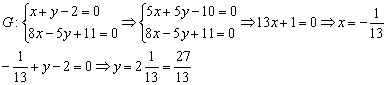
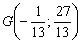
А сейчас рассмотрим более редкие задания. Треугольник тот же.

9) найти уравнение биссектрисы ;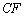
10) найти центр тяжести 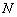треугольника;
11) составить систему линейных неравенств, определяющих треугольник.

Как найти уравнение биссектрисы треугольника?

9) Биссектриса делит угол пополам. Чтобы были более понятны последующие выкладки, я сразу приведу готовый чертёж с результатом:

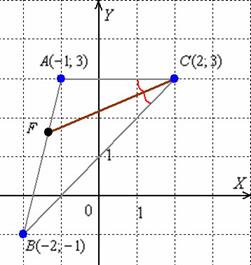
Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков:

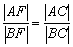
Длины сторон уже найдены в предыдущих пунктах: .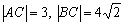

Таким образом: 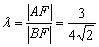. Координаты точки 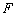найдём по формулам деления отрезка в данном отношении. Да, параметр «лямбда» получился просто сказочным, а кому сейчас легко?

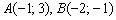
Понеслась нелёгкая:

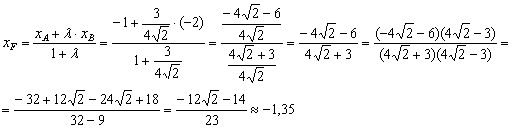
На последнем шаге я провёл умножение числителя и знаменателя на сопряжённое выражение 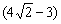– чтобы использовать формулу 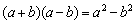и избавиться от иррациональности в знаменателе.

Разбираемся со второй координатой:

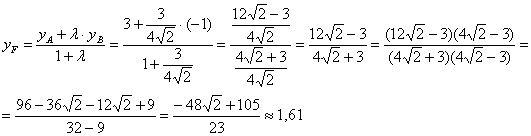
Таким образом: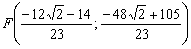

Предчувствие вас не обмануло, уравнение биссектрисы 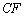составим по точкам