Линейное уравнение с постоянными коэффициентами

Рассмотрим линейное уравнение с постоянными коэффициентами:

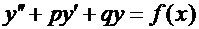(16)

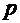( и 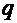– постоянные числа), и соответствующее ему однородное уравнение

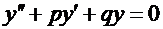. (17)

Определение. Характеристическим уравнением, соответствующим дифференциальному уравнению (17), называется алгебраическое квадратное уравнение

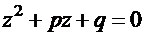. (18)

Отметим, что второй производной 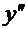дифференциального уравнения соответствует в характеристическом уравнении 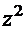. Коэффициент при первой производной 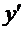переходит в коэффициент при первой степени 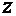. Наконец, коэффициент при 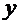, то есть при производной нулевого порядка, переходит в свободный член (коэффициент при нулевой степени ).

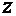Примеры.1. Для линейного однородного уравнения 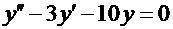соответствующее характеристическое уравнение записывается в виде .

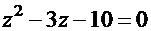2. Уравнению 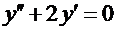соответствует характеристическое уравнение .

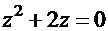3. Уравнению 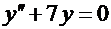соответствует характеристическое уравнение .

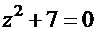Общее решение однородного уравнения (17) можно получить, исходя из корней соответствующего характеристического уравнения (17). Здесь возможны три случая в соответствии с возможным значением его дискриминанта .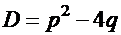

А. Случай положительного дискриминантаПусть 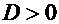. В этом случае уравнение (18) имеет два различных вещественных корня 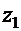и :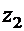

,

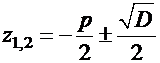что соответствует разложению квадратного трехчлена на множители с вещественными коэффициентами:

.

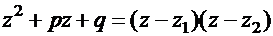Можно проверить, что в этом случае общее решение однородного уравнения (16) имеет вид:

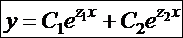. (19)

Примеры. 1. 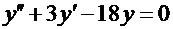; начальные условия: 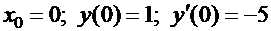. Соответствующее характеристическое уравнение: 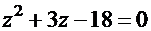. Дискриминант 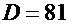. Корни квадратного уравнения 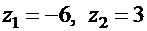. Общее решение имеет вид: .

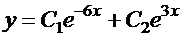Найдем частное решение для задачи Коши.

Дифференцируем общее решение: 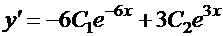. Подставляем начальные условия в 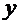и 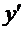(учитывая, что ):

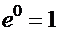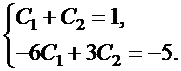
Решая эту систему, получаем: 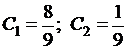. Соответствующее решение задачи Коши: .

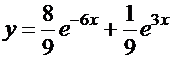2. 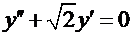. Характеристическое уравнение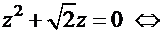 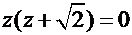. Корни квадратного уравнения 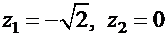. Общее решение имеет вид: .

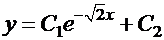Б. Случай нулевого дискриминантаПусть 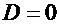. В этом случае характеристическое уравнение имеет один вещественный корень кратности :

,

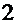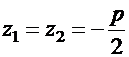что соответствует разложению квадратного трехчлена на множители с вещественными коэффициентами:

.

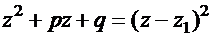Можно проверить, что в этом случае общее решение однородного уравнения (17) имеет вид:

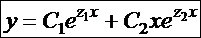. (20)

Пример. 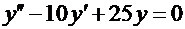. Соответствующее характеристическое уравнение 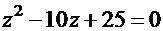. Дискриминант 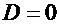. Кратный корень квадратного уравнения 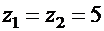. Общее решение имеет вид: .

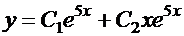В. Случай отрицательного дискриминантаПусть 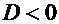. В этом случае уравнение (17) имеет два различных комплексных корня 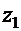и 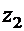, которые задаются формулой:

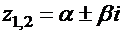, где .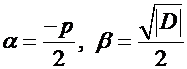

К этим значениям можно придти, используя формально выражение для корней, полученное в случае положительного дискриминанта, и помня, что 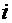обозначает «мнимую единицу» —комплексное число, для которого :

.

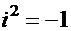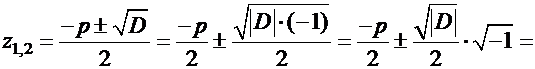
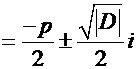Можно проверить, что в этом случае общее решение однородного уравнения (17) имеет вид:

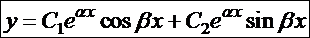. (21)

Примеры. 1. 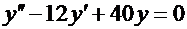. Соответствующее характеристическое уравнение 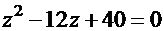. Дискриминант 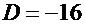. Корни квадратного уравнения 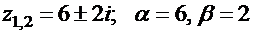. Общее решение имеет вид: .

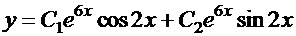2. 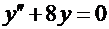. Соответствующее характеристическое уравнение 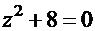. Корни квадратного уравнения 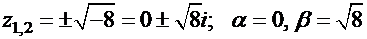. Общее решение имеет вид: .

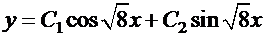Найдем частное решение для задачи Коши с начальными условиями 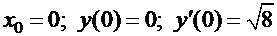. Дифференцируем общее решение:

.

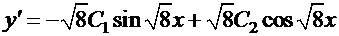Подставляем начальные условия в 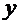и 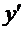(учитывая, что ):

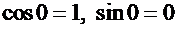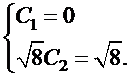
Отсюда 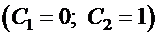. Соответствующее частное решение .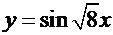