Вариационное исчисление. Метод вариации в задачах с неподвижными границами.

В задачах физики иногда возникает необходимость найти максимальные и минимальные значения величин, которые зависят от одной или нескольких функций.

Определение 1:

Функционалом называют переменную величину 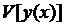, зависящую от функции 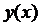, если 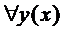из некоторого класса функций соответствует значение 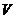, т.е. имеет место соответствие: функции 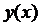соответствует число .

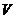Аналогично определяются и функционалы, зависящие от нескольких функций или зависящие от функций нескольких независимых переменных.

Простейшим примером является длина 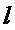дуги кривой, соединяющей две заданные точки 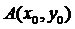и

.

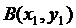
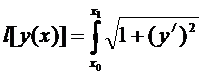Площадь 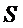некоторой поверхности также является функционалом, так как она определяется выбором :

,

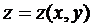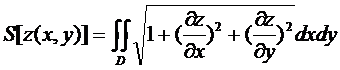где 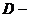проекция поверхности на плоскость .

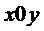Моменты инерции, статические моменты, координаты центра тяжести некоторой однородной кривой или поверхности также являются функционалами, так как определяются выбором функций, которые определяют кривые или поверхности.

Вариационное исчисление изучает методы, которые позволяют находить максимальные и минимальные значения функционалов.

На развитие вариационного исчисления как самостоятельной математической дисциплины оказали влияние три задачи:

1) Задача о брахистохроне: задача о линии наибыстрейшего ската, которая называется брахистохроной (Иоганн Бернулли, 1689). Эта линия, соединяющая две заданные точки, не лежащие на одной вертикальной прямой, и по которой материальная точка скатится за кратчайшее время. Оказалось, что линией быстрейшего ската является циклоида.

2) Задача о геодезических линиях.

Найти линию наименьшей длины, соединяющая две заданные точки на некоторой поверхности 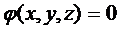. Такие линии называются геодезическими.

Найдём минимум функционала:

,

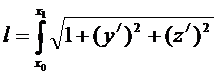где 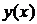и 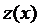удовлетворяют условию .

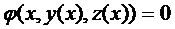3) Изопериметрическая задача:

Требуется найти линию заданной длины, ограничивающую максимальную площадь .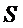

Чаще всего рассматривают следующие основные вариационные задачи:

,

,

,

.

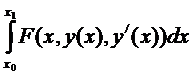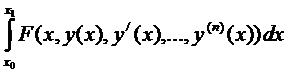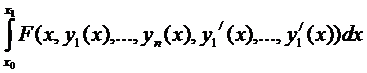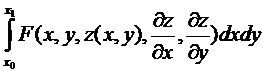Вариация и её свойства.

Определение 2:

Приращением или вариацией 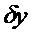аргумента 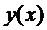функционала 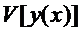называется разность между двумя функциями 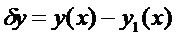, где 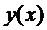меняется произвольно в некотором классе функций.

Определение 3:

Функционал 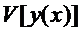непрерывен при 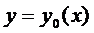в смысле близости 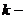ого порядка, если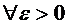 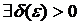такое, что имеет место неравенство

при

,

,

…

.

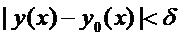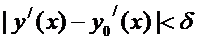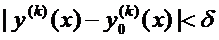Функция 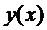берётся из класса функций, на котором функционал 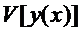определён.

Определение 4:

Функционал называется линейным 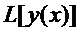, если выполняются следующие условия:

1. 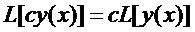, где 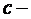постоянная.

2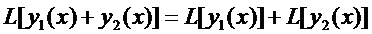

Например, .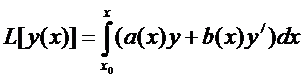

Определение 5:

Если приращение функционала 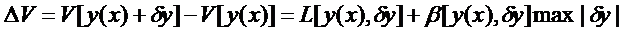представимо в таком виде, где 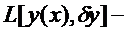линейный по отношению к 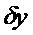функционал и при 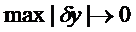, то линейная по отношению к 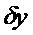часть приращения функционала, т.е. 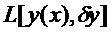называется вариацией функционала и обозначается .

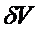Итак, вариация функционала – это главная, линейная по отношению к 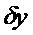часть приращения функционала.

При исследовании функционалов, вариация играет ту же роль, что и производная при исследовании функций.

Вообще говоря, упрощения исследования функционалов дают почти эквивалентное определение вариации функционала.

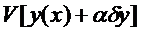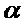по при 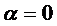, т.е. .

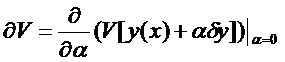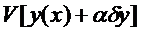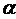Действительно, производная от по при 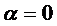равна:

.

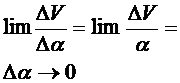
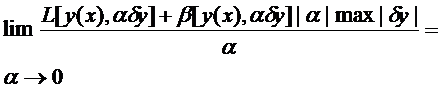
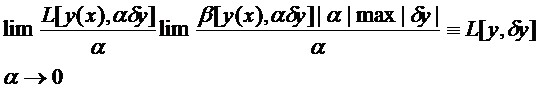Так как 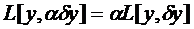, а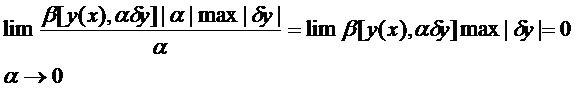

Если существует вариация в смысле главной части приращения функционала, то существует и вариация в смысле производной по параметру при 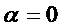. Второе определение несколько шире первого, так как не всегда можно выделить главную линейную часть приращения функционала.

Определение 6:

Функционал 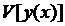достигает на кривой 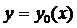максимума(минимума), если значения функционала 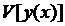на любой близкой от 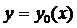кривой, больше(не меньше), чем 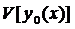, т.е. .

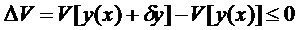Есл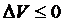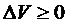и ( ) и 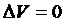только при , то говорят, что на кривой 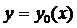достигается строгий максимум (минимум).

Теорема:

Если функционал 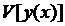, имеющий вариацию, достигает максимума или минимума при 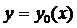, где 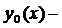внутренняя точка область определения функционала, то при , .

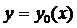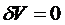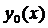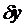При одинаковых и функционал 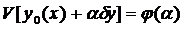является функцией от 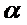, которая при 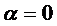по предположению имеет максимум или минимум. Тогда 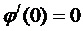или

,

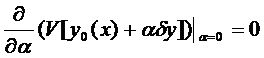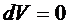
В определении максимума или минимума надо указывать, какого порядка близость имеется в виду. Если функционал достигает максимума или минимума по отношению ко всем кривым, для которых 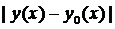мал, то максимум или минимум называется сильным.

Если же лишь по отношению к кривым, близким к 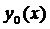в смысле близости первого порядка, т.е. ещё мал и 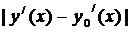, то максимум или минимум называется слабым.

Замечание:

Если на кривой 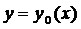достигается экстремум, то не только ,

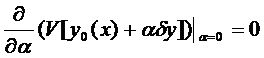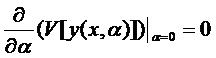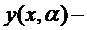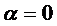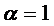но и , где любое семейство допустимых кривых, причём при и функция 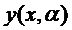должна приращаться в 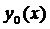и 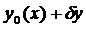. Эта производная, конечно, не совпадает с вариацией функционала, но обращается в нуль одновременно с 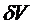, на кривых, реализующих экстремум функционала, это будет использовано в дальнейшем при исследовании функционалов на экстремум.

ЛЕКЦИЯ 15: