Раздел 1. Векторная и линейная алгебра.
Раздел 1. Векторная и линейная алгебра.
Лекция 1. Матрицы, операции над ними. Определители.
- Определения матрицы и транспонированной матрицы.
- Что называется порядком матрицы? Если в матрице 3 строки и 5 столбцов, то каков ее порядок? Порядок транспонированной матрицы?
- Какая матрица называется квадратной? Единичной?
- Определение суммы матриц. Можно ли сложить матрицы A порядка
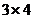и B порядка 
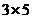? - Определение умножения матрицы на число. Пусть
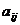- элементы матрицы A. Каковы элементы матрицы 4A? - Умножение матриц. Матрицы каких порядков можно перемножать?
- Существуют ли произведения матриц AB и BA, если матрица A имеет порядок 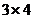, а B -
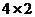? - Чему равно произведение матриц EA?
- Для каких матриц существуют определители? Определитель – это число или матрица?
- Правило вычисления определителей 2 порядка.
- Правило треугольников и правило дополнения (Саррюса) для определителей 3 порядка.
Лекция 2. Свойства определителя квадратной матрицы. Обратная матрица.
- Определитель – это матрица или число?
- В каких случаях определитель равен нулю?
- Если k строк определителя умножить на одно и тоже число n, то как изменится определитель?
- Определения минора и алгебраического дополнения элемента матрицы.
- В разложение определителя по элементам строки входят миноры или алгебраические дополнения?
- Что такое невырожденная (неособая) квадратная матрица?
- Определение обратной матрицы.
- Почему обратную матрицу может иметь только невырожденная матрица?
- Имеет ли обратную матрицу прямоугольная матрица порядка ?
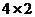- Имеет ли обратную матрицу матрица
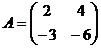и почему?
Лекция 3. Системы линейных алгебраических уравнений.
- Чем отличается однородная система от неоднородной?
- В матричной записи системы
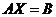каково число столбцов в матрицах 
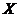и 
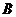? - Что такое определитель системы?
- Определение решения системы.
- Какие системы называются совместными?
- Можно ли использовать правило Крамера при решении системы 3 линейных уравнений с четырьмя неизвестными?
- Можно ли использовать правило Крамера, если определитель системы равен нулю и почему?
- Можно ли использовать метод Гаусса при решении системы 3 линейных уравнений с четырьмя неизвестными?
- Изменяют ли эквивалентные преобразования расширенной матрицы в методе Гаусса решение системы?
- Можно ли решать систему с помощью обратной матрицы, если определитель системы равен нулю и почему?
Лекция 4. Векторы.
- Чем отличаются векторные величины от скалярных? Ускорение – это векторная величина или скалярная?
- Определение вектора, его модуля. Может ли модуль вектора быть меньше нуля?
- Что такое коллинеарные векторы? Компланарные векторы?
- Может ли начало радиус-вектора лежать в точке А(1,0)?
- Какие векторы называются свободными?
- Как находятся координаты вектора?
- Определения суммы и разности двух векторов.
- Можно ли вычитать векторы разных размерностей?
- Сформулируйте правило параллелограмма.
- Как расположены и как направлены векторы
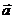и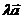 
, если 
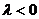? - Понятие базиса системы векторов. Является ли базисом система двух коллинеарных векторов на плоскости? Система трех компланарных векторов в пространстве?
- Три формы записи вектора в пространстве.
Лекция 9. Предел функции.
- Определение ограниченной функции.
- Определение бесконечно малой функции.
- Определение предела функции в точке. Геометрический смысл.
- Определение предела функции в бесконечности. Геометрический смысл.
- Определения последовательности и ее предела.
- Записать связь предела и бесконечно малой функции.
- Может ли функция иметь два предела?
- Арифметические действия над пределами.
- Предельный переход в неравенствах.
- Записать четыре вида 1 замечательного предела. Какую неопределенность представляет из себя 1 замечательный предел?
- Запишите два вида второго замечательного предела. Какую неопределенность он из себя представляет?
- Какие бесконечно малые называются эквивалентными? Что такое О (о большое) и о (о малое)?
Раздел 1. Векторная и линейная алгебра.