Теоретико-множественный смысл натурального числа.
Натуральное число– есть общее свойство класса конечных равномощных между собой множеств.
Нуль - общее свойство пустого множества, количество элементов в пустом множестве. 0=n(Ø)
Определение отношения «меньше» для натуральных чисел:
Число а меньше b тогда и только тогда, когда при счете число а называют раньше числа b.
Определение отношения «меньше» с теретико-множественной позиции:
Пусть а-число элементов в множестве А, а b-число элементов в множестве B, тогда а будет меньше b тогда и только тогда, когда множество А равномощно отрезку натурального ряда Na, а множество B равномощно отрезку натурального ряда Nb и отрезок натурального ряда Na является собственным подмножеством отрезка натурального ряда Nb.
Пример: Почему 5<7? 5<7, т.к. N5 С N7. 5 не больше 7, т.к. N7 не является подмножеством N5.
Теоретико-множественный смысл отношения «меньше»: а меньше b в том случае, когда отрезок натурального ряда (Na) является собственным подмножеством натурального ряда (Nb)
3 ВОПРОС:Истомина 1 кл.1ч. с. 30 «больше». С.28 «меньше»
Теоретико-множественный смысл суммы натуральных чисел. Свойства сложения, их теоретико-множественный смысл. Словесные формулировки свойств сложения, изучаемых в начальной школе. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл суммы натуральных чисел.
Сложение целых неотрицательных чисел связано с объединением конечных непересекающихся множеств. Например, если множество А содержит 5 элементов, а множество В – 4 элемента и пересечение множеств А и В, пусто, то число элементов в их объединении равно сумме 5 + 4.
Теорема. Пусть А и В — конечные множества, не имеющие общих элементов. Тогда их объединение тоже конечно, причем n(A и B) =п(А) + n(B). Доказательство. Докажем сначала, что если a и b натуральные числа, то существует взаимно-однозначное отображение отрезка натурального ряда Nа на множество X таких чисел, что а + 1 =<х=<а + b. Действительно, если поставить в соответствие числу с ? Nb число с + а, то в силу монотонности сложения этим будет задано взаимно однозначное отображение отрезка Nb на множество X. Например, если а = 3, b = 5, то соответствие между множествами N5 и X = {4, 5, 6, 7, 8} может быть установлено так: числу с ? N5 сопоставим число х = 3 + с; числу 1 - число 3 + 1=4, числу 2 - число 3 + 2 = 5 и т.д., числу 5 - число 2 + 5 = 8.
Пусть п (А) = а, п (В) = b. Тогда существуют взаимно однозначные отображения А на Nа и В на Nb. Но согласно доказанному выше, отрезок Nb можно взаимно однозначно отобразить на множество X таких чисел, что а + 1 <х<а + Ъ. Тем самым множество В взаимно однозначно отображается на X. Отображая взаимно-однозначно множество А на Na, множество В на X, получаем взаимно - однозначное отображение множества А объедин. В на отрезок Na+b Поскольку нет элементов, одновременно принадлежащих А и В, то это отображение определено на всем множестве А объедин. В. Значит, в множестве А объедин. В имеется а +b элементов, что и требовалось доказать. Из рассмотренной теоремы следует, что
Теоретико-множественных позиций сумма натуральных чисел а и в представляет собой число элементов в объединении конечных непересекающихся множеств А и В таких, что а = n(A), b = n(B): а + в = n(A) + n(B) = n(A È B), если А Ç В = Æ.
Словесные формулировки свойств сложения, изучаемых в нач школе:
- Переместительный закон (коммутативный) – от перемены мест слагаемых сумма не меняется a+b=b+a
- Сочетательный закон (ассоциативный) – сумма не зависит от порядка выполняемых действий или 2 соседних слагаемых можно заменить значением их суммы (a+b)+c= a+(b+c)
Пример: «Катя нашла 3 гриба, а Маша – 4. Сколько всего грибов нашли девочки?»
В задаче рассматриваются три множества: множество А грибов Кати, множество В грибов Маши и их объединение. Требуется узнать число элементов в этом объединении, а оно находится сложением. Так как n(А) = 3, n(В) = 4 и А Ç В= Æ, то n(A È B) = 3 +4. Сумма 3 + 4 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи: 3 + 4 = 7. Следовательно, девочки нашли 7 грибов.
3 ВОПРОС:Истомина 1 кл.1ч. с.66
Определение вычитания натуральных чисел через сложение. Теоретико-множественный смысл разности натуральных чисел. Условие существования разности в множестве натуральных чисел. Правила вычитания числа из суммы и суммы из числа. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл разности натуральных чисел.
Натуральные числа — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Разность целых не отрицательных чисел а - в, называется такое целое неотрицательное число, что: а = в + с.
8 – 6 = 2 т. к. 6 + 2 = 8
С теоретико-множественной позиции разность натуральных чисел a и b представляет собой число элементов в дополнении множества B до множества A, если а = n(A), (целое неотрицательное число определяющее число элементов в множестве А) b = n(B) (целое неотрицательное число определяющее число элементов в множестве В) и BСA (Множество В, является подмножеством множества А).
а = n(A)
 b = n(B)
b = n(B)
 BСA
BСA
а – в = n(B\A)
Пример:
7 – 2 = n(B\A) = 5
7 = n(A)
2 = n(B)
BСA
Условие существования разности натуральных чисел: разность натуральных чисел a и b существует тогда и только тогда, когда b 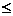 a и эта разница единственна.
a и эта разница единственна.
Правило вычитания числа из суммы и суммы из числа, их теоретико-множественная интерпретация.
Взаимосвязь вычитания чисел и вычитание множеств позволяет обосновать выбор действия. Чтобы узнать, насколько одно число меньше или больше другого, надо из большего числа вычисть меньшее.
Взаимосвязь действий над числами, теоретико-множественный смысл отношений «меньше на и больше на» позволяют обосновывать выбор действий при решении задач с этими отношениями.
1. Вычитание числа из суммы:
Правило вычитания числа из суммы: чтобы вычесть число из суммы достаточно вычесть это число из любого слагаемого и полученному результату прибавить оставшееся слагаемое(другое, которое еще не задействовано).
Теор.множ.трактовка этого правила:
Для трех конечных мн-в А, В и С, таких, что а=n(А), в=n(В) и с=n(С), A 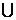 B= Ø, С
B= Ø, С 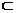 А
А
имеет место равенство: (А U В) \ С=(А\С) В, из этого следует, что число элементов в этой разности n((А 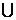 В) \ С) равно разности элементов из объединения – число элементов во мн-ве С: n((А
В) \ С) равно разности элементов из объединения – число элементов во мн-ве С: n((А 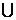 В) \ С)=n(А\C)
В) \ С)=n(А\C) 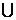 B) = (а+в)-с=(а-с)+в n(А\C)+n(В) = (а-с)+в
B) = (а+в)-с=(а-с)+в n(А\C)+n(В) = (а-с)+в
2.Вычитание суммы из числа:
a - (b + c) = a - b - c (при а >= b + c)
Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности - второе слагаемое.
Теоретико-множественная интерпретация правила вычитания суммы из числа: для трёх конечных множеств А, В, С таких, что a=n(A), b=n(B), c=n(C), B 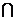 C=
C= 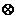 , B
, B 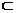 A и C
A и C 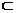 A, тогда имеет место равенство: A\(B
A, тогда имеет место равенство: A\(B 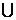 C)=(A\B)\C) из этого следует, что: n(A\(B
C)=(A\B)\C) из этого следует, что: n(A\(B 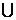 C))=n(A)\n(B
C))=n(A)\n(B 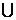 C)=n(A)- n(B
C)=n(A)- n(B 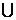 C)=a-(b+c)
C)=a-(b+c)
1. Если из числа вычесть нуль, оно не изменится.
2. Если из числа вычесть это число, получится нуль.
3 ВОПРОС:Истомина 1 кл.1ч.с,88
Определение умножения натуральных чисел через сложение. Теоретико-множественный смысл произведения. Свойства умножения. Словесные формулировки свойств умножения, изучаемых в начальной школе. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл умножения натуральных чисел.
Натуральные числа — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
