Решение линейных дифференциальных уравнений 2-го порядка с

Постоянными коэффициентами

5.1. Линейные дифференциальные уравнения 2-го порядка.

Уравнение вида

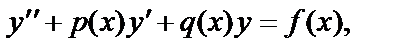(19)

где p(x), q(x) и f(x) – заданные функции, называется линейным дифференциальным уравнением 2-го порядка.

Отличительной его особенностью является то, что искомая функция у, и ее производные 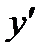и 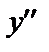входят в уравнение в первых степенях и не перемножаются между собой, т.е. связаны линейно.

Если 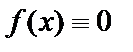, то уравнение (19) называется линейным однородным дифференциальным уравнением и имеет вид:

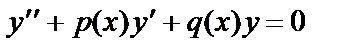. (20)

если же 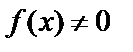, то уравнение (19) называется линейным неоднородным дифференциальным уравнением 2-го порядка.

Общее решение линейного однородного уравнения 2-го порядка (20) имеет вид:

,

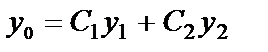где у₁ и у₂ – два линейно независимых частных решения этого уравнения 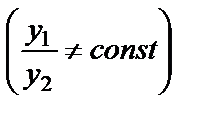, а С₁ и С₂ – произвольные постоянные.

Общее решение линейного неоднородного уравнения (19) имеет вид:

,

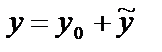где 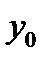– общее решение соответствующего однородного уравнения (20), а 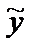– какое-либо частное решение неоднородного уравнения (19).

5.2. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

Если коэффициенты при у, 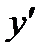и 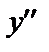– постоянные, то уравнение

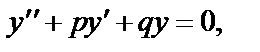(21)

где p и q – вещественные числа, называется линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами.

Общее решение уравнения (21) имеет вид: ,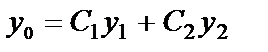

где у₁ и у₂ – два линейно независимых частных решения этого уравнения, а С₁ и С₂ – произвольные постоянные.

Для нахождения линейно независимых частных решений у₁ и у₂ уравнения (21) используется квадратное уравнение вида

,

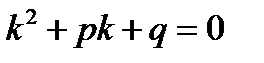которое называется характеристическим для уравнения (21).

В таблице 1 приведены виды функций у₁ и у₂ и вид общего решения уравнения (21) в зависимости от вида корней характеристического уравнения.

Таблица 1.

Корни характеристического уравнения	Вид функций у1 и у2	Вид общего решения уравнения
Вещественные различные	,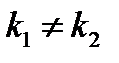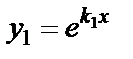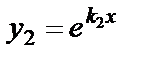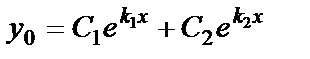
Вещественные равные	,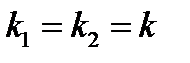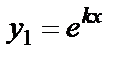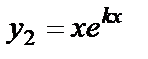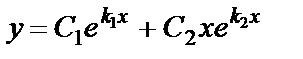
Комплексно-сопряженные	,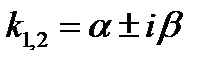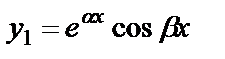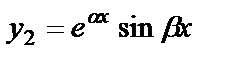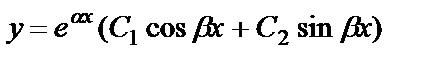

Пример 5. Найти общее решение уравнения .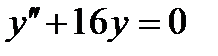

Решение. Характеристическое уравнение для данного однородного уравнения имеет вид 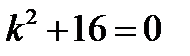(коэффициент при 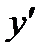равен нулю). Его корнями являются комплексные числа 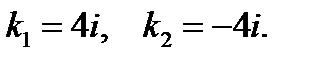Здесь 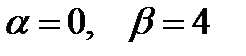. Тогда 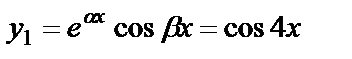, 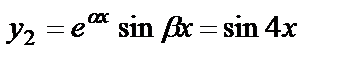и общее решение данного уравнения: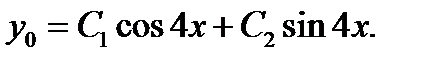

Ответ: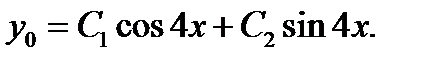

5.2. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

Уравнение вида

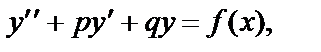(22)

где p и q – вещественные числа, называется линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами.

Общее решение линейного неоднородного уравнения (22) имеет вид:

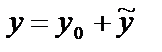(23)

где 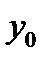– общее решение соответствующего однородного уравнения (21), а 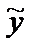– какое-либо частное решение неоднородного уравнения (22).

Построение общего решения неоднородного уравнения состоит из двух этапов. Сначала нужно найти общее решение соответствующего однородного уравнения 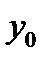, затем найти частное решение 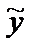неоднородного уравнения.

Решение 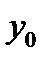для линейного однородного дифференциального уравнения (21) находят, используя характеристическое уравнение (п. 5.1), а для нахождения частного решения 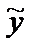уравнения (22) можно использовать либо метод вариации произвольных постоянных, либо метод неопределенных коэффициентов.

Метод вариации произвольных постоянных.

Метод вариации произвольных постоянных применяется для нахождения частного решения 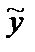линейного неоднородного дифференциального уравнения в тех случаях, когда известно общее решение 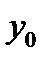соответствующего однородного уравнения.

Если известно 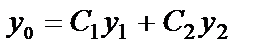, то функция 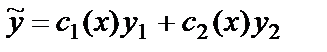будет частным решением уравнения 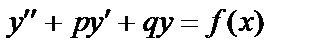, если функции с₁(х) и с₂(х) удовлетворяют так называемым «условиям вариации»:

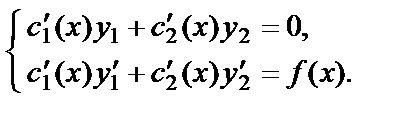(24)

Для нахождения частного решения 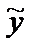необходимо решить систему уравнений (24), затем проинтегрировать полученные функции:

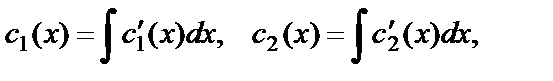(25)

и записать частное решение: 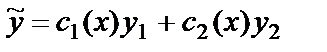. Константы интегрирования в (25) можно взять равными нулю, т.к. мы находим частное решение.

Пример использования метода вариации произвольных постоянных приведен в образце выполнения контрольной работы.

Метод неопределенных коэффициентов.

Метод неопределенных коэффициентов применяется для нахождения частного решения 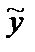неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f(x), стоящая в правой части этого уравнения, имеет один из двух «специальных» видов:

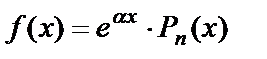, (26)

где P_n(x) – многочлен степени n: P_n(x) = a₀ xⁿ + a₁ x^n-1 +….+ a_n-1 x+ a_n,

или

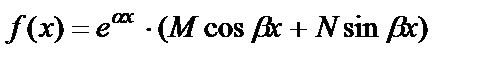, (27)

где M и N – числа.

1) Если 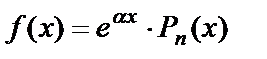, то частное решение можно искать в виде:

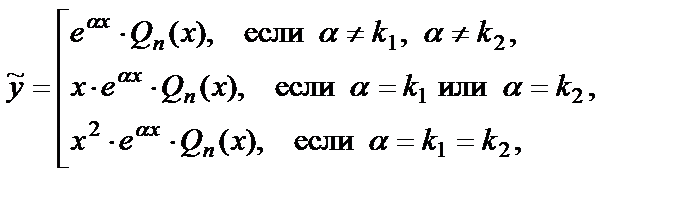(28)

где k₁, k₂ – корни характеристического уравнения, Q_n(x) – многочлен степени n, записанный с неопределенными коэффициентами, подлежащими определению, например,

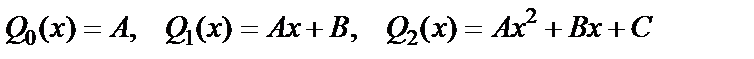, и т.д.

2) Если 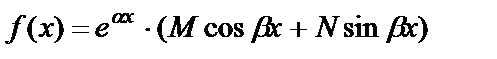, то частное решение можно искать в виде:

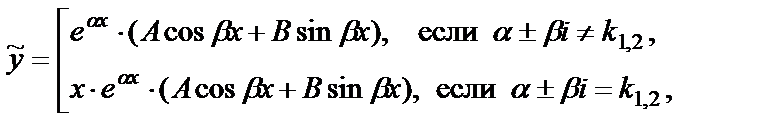(29)

где k₁, k₂ – корни характеристического уравнения, А и В – неизвестные постоянные, подлежащие определению.

Пример 6. Найти общее решение уравнения .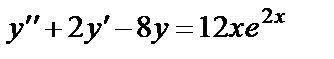

Решение.

1 этап. Построим общее решение 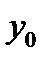соответствующего однородного уравнения 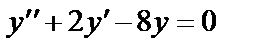. Составим для него характеристическое уравнение 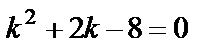и найдем корни: 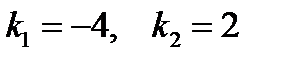– корни вещественные и различные. По таблице 1 определим вид линейно независимых частных решений однородного уравнения: 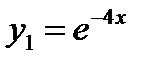, 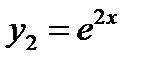и запишем его общее решение:

.

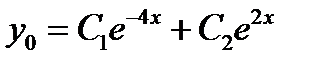2 этап. Построим частное решение данного неоднородного уравнения 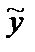. В заданном уравнении 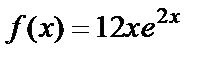– правая часть 1-го специального вида: 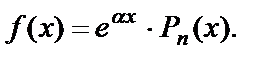Здесь 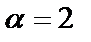, P_n(x) = 12x, т.е. многочлен в правой части – 1-й степени (n = 1). Число 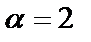совпадает с корнем характеристического уравнения 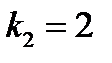. Следовательно, согласно (28) частное решение 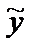будем искать в виде:

,

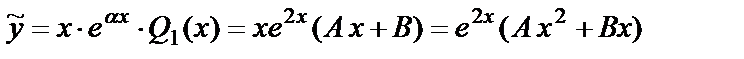где А, B – неизвестные коэффициенты, подлежащие определению.

Найдем производные 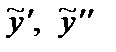и подставим 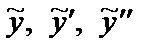в данное неоднородное уравнение 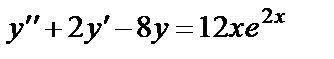, при этом для простоты используем следующую форму записи:

.

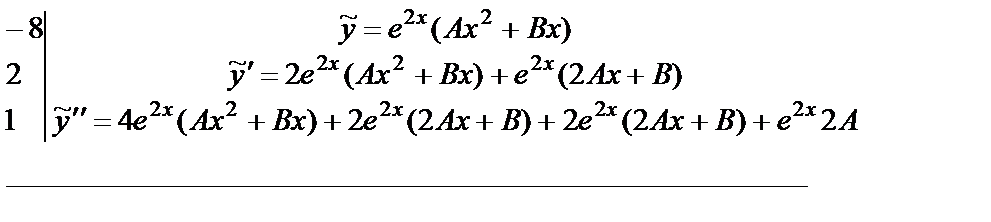
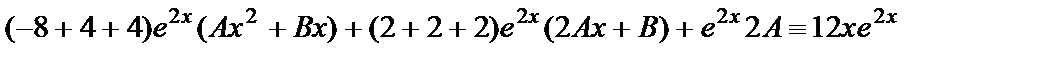Здесь слева от черты записаны коэффициенты, с которыми 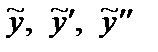входят в уравнение, а под чертой приравниваются (тождественно) левая и правая части уравнения после подстановки в него .

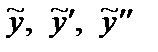После сокращения обеих частей тождества на 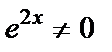, получаем:

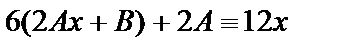, откуда, приравнивая коэффициенты при х¹ и при х⁰ в обеих частях тождества, получаем: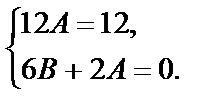

Решая систему, находим 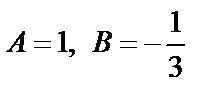. Подставляя найденные значения в 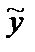, получим: .

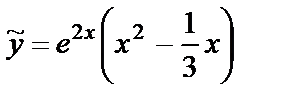Объединяя результаты 2-х этапов, получаем общее решение уравнения: .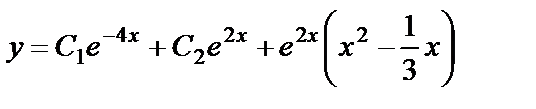

Ответ: .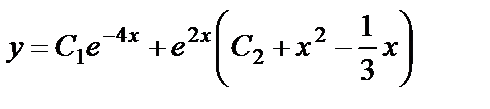

Пример использования метода неопределенных коэффициентов для случая, когда функция, стоящая в правой части уравнения, имеет 2-й специальный вид, приведен в образце выполнения контрольной работы.