Элементы теории случайных величин
Величина x является случайной, если при каждом повторном ее наблюдении она принимает различные значения.
Различают дискретные и непрерывные случайные величины.
Дискретная случайная величина может принимать лишь дискретные значения.
Непрерывная случайная величина принимает значения из некоторого интервала, причем всевозможные, число таких значений бесконечно.
Основной характеристикой непрерывной случайной величины является функция распределения случайной величины. Различают две функции распределения: интегральную 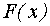 и дифференциальную
и дифференциальную 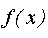 функции распределения.
функции распределения.
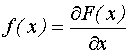
f(x) - дифференциальная функция распределения случайной величины
F(x) - интегральная функция распределения случайной величины
| Интегральной функцией распределения F(x) называется неубывающая функция вида (для положительных случайных величин) F(X)=P(x<X) | 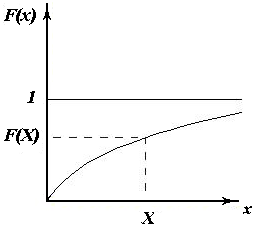 |
Вероятность данного значения случайной величины - это отношение числа, которое определяет, сколько раз случайная величина принимает данное значение к числу испытаний. Это определение называется частотой 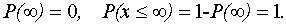
Дифференциальная функция распределения f(x): Основное свойство дифференциальной функции распределения f(x): 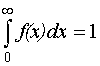 | 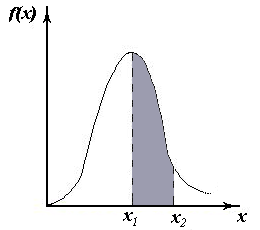 |
Вероятность того, что 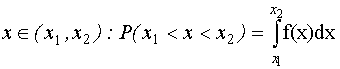

Вероятность конкретного значения непрерывной случайной величины не определена. Из определения вероятности вытекает основное свойство дифференциальной функции распределения f(x).
Наибольшее распространение в теории вероятности получило так называемое нормальное распределение (распределение Гаусса).
Дифференциальная функция распределения для распределения Гаусса имеет вид:
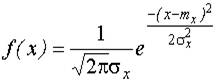 , , , , | где 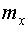 - математическое ожидание случайной величины; - математическое ожидание случайной величины; 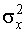 - дисперсия случайной величины (характеристика разброса случайных значений относительно математического ожидания); - дисперсия случайной величины (характеристика разброса случайных значений относительно математического ожидания); 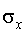 - среднеквадратичное отклонение (СКО) случайной величины: - среднеквадратичное отклонение (СКО) случайной величины: 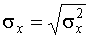 |
Размерность математического ожидания и среднеквадратичного отклонения совпадают с размерностью случайной величины, а размерность дисперсии - квадрат размерности случайной величины.
Сравним две случайные величины:
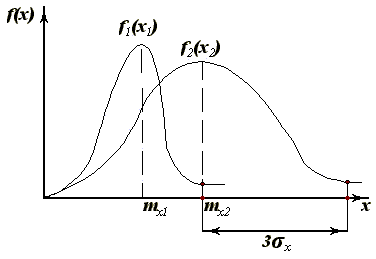 | Для нормального распределения 95% значений случайной величины укладываются в 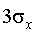 . . |
Кроме функции распределения, случайная величина характеризуется моментными характеристиками (моментами). Существуют начальные и центральные моменты.
Начальным моментом k-го порядка 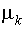 называется выражение: называется выражение: | 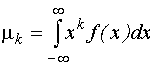 |
Центральным моментом k-го порядка 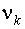 называется выражение: называется выражение: | 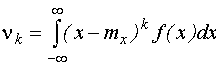 |
| Величина математического ожидания, равная нулю, называется центрированной случайной величиной. | 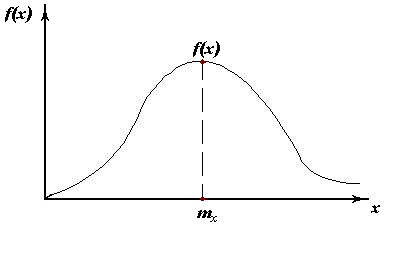 |
| Математическое ожидание и дисперсия случайной величины являются соответственно начальным моментом 1-го порядка и центральным моментом 2-го порядка. | 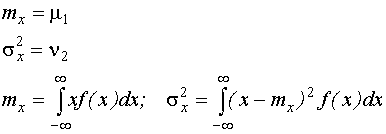 |
Пример.
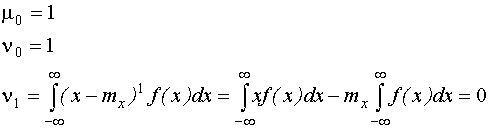
Моментные характеристики случайной величины не могут быть определены непосредственно по данным выражениям, так как необходимо знать дифференциальную функцию распределения случайной величины.
Если имеется выборка значений случайной величины, то на основе этой выборки могут быть даны оценки моментной характеристики.
| Оценка математического ожидания определяется как среднее значение всех значений: | 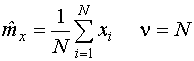 |
| Оценка дисперсии: | 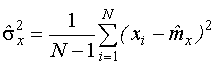 |
При вычислении оценки в знаменателе используется число степеней свободы ( 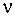 ).
). 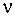 определяется как разность между объемом выборки и числом наложенных связей, то есть числом обращений к исходной выборке с целью вычисления оценок, найденных по той же выборке при вычислении данной оценки. Для математического ожидания
определяется как разность между объемом выборки и числом наложенных связей, то есть числом обращений к исходной выборке с целью вычисления оценок, найденных по той же выборке при вычислении данной оценки. Для математического ожидания 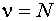 , для дисперсии
, для дисперсии 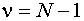 .
.
Свойства оценок
Оценки характеристик случайных величин, как и другие оценки, характеризуются следующими свойствами:
1. смещенность или несмещенность;
2. состоятельность или несостоятельность;
3. эффективность или неэффективность.
Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине
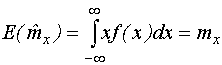
E - символ математического ожидания.
В противном случае оценка называется смещенной.
Оценка называется состоятельной, если выполняется следующее условие:
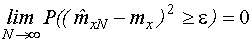
Свойство состоятельности заключается в том, что с ростом объема выборки точность оценки увеличивается.
Оценка называется эффективной, если ее дисперсия минимально возможная: