Свободные колебания системы с произвольным числом степеней свободы

Динамика сооружений - это один из специальных разделов строительной механики, посвященный методам расчета сооружений на динамические нагрузки. Динамические нагрузки по своей природе весьма разнообразны. К такого рода воздействиям относятся природные явления, т.е. сейсмические толчки, ветровые порывы, а также различные динамические воздействия технологического или аварийного происхождения: движение неуравновешенных частей машин и механизмов; падение летящего тела при соударение его с элементами конструкций; работа копров, молотов и других ударных механизмов; движение поездов, кранов и т.д.

Особенностью динамических нагрузок является то, что при их действии сооружение переходит в состояние движения, причем при периодическом повторении динамических воздействий в определенных условиях происходит накопление энергии системы, выра­жающееся в постепенном увеличении амплитуды колебаний.

Это явление, называемое резонансом, особенно опасно для сооружения тем, что разрушение может произойти и при воздействиях с малой интенсивностью.

Существенным отличием динамических методов расчета от статических является введение в уравнениях состояния нового пере­менного - времени и, ввиду их значительности, инерционных сил. При этом, если при решении аналогичных задач при статическом нагружении, уравнения состояния выражались при помощи алгебраических или трансцендентных уравнений, то соответствующая динамическая задача требует уже решения дифференциальных уравнений с производными по времени.

В динамике сооружений следует различать два типа движения или колебания системы. Колебания системы при отсутствии действия внешних сил называются свободными. Если колебания системы сопровождаются действием внешних динамических нагрузок, то колебания называются вынужденными.

Для описания динамических колебаний необходимо ввести в рассмотрение следующие понятия: круговая частота w и пе­риод колебаний 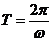. Круговая частота определяет число циклов колебания в течении 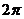секунд, а период определяет интервал времени, в течении которого совершается полный цикл колебаний.

Системы в динамике сооружений различаются по числу степеней свободы. Числом степеней свободы системы называется число независимых геометрических параметров (обобщенных координат), определяющих положение системы (материальных точек) в любой момент времени при ее (их) движении. Число степеней свободы системы складывается из числа степеней свободы материальных точек, принадлежащих системе. Число степеней свободы является основной характеристикой системы при динамических воздействиях.

В динамике сооружений различают два основных подхода: кинетостатический и энергетический.

Кинетостатический подход состоит в том, что сооружение в произвольный момент времени предполагается находящимся в равновесном состоянии под действием заданных динамических и вызванных ими инерционных нагрузок. Далее для составления уравнений состояния применяются классические методы строительной механики (метод сил, перемещений или смешанный).

Энергетический подход основан в определении в равновесном состоянии через закон сохранения энергии с учетом инерционных сил. В частности, когда силы сопротивления движению не учитываются, энергетический принцип в общем случае записы­вается в виде:

,

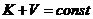где K - кинетическая энергия системы; V - потенциальная энергии системы или работа внешних или внутренних сил, так как система в процессе колебания находится в равновесном состоянии.

В настоящей книге при решении конкретных задач ограничимся применением кинетостатического подхода, а для вывода уравнения - метода сил.