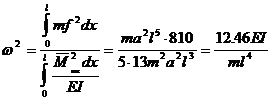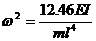Колебания систем с бесконечным числом степеней свободы.

Теория механических колебаний имеет многозначисленные и весьма разнообразные приложения едва ли не во всех областях техники. Независимо от назначения и конструктивного решения различных механических систем их колебания подчиняются одним и тем же физическим закономерностям, изучение которых и составляет предмет теории колебаний упругих систем. Наиболее полно разработана линейная теория колебаний. Теория колебаний систем с несколькими степенями свободы была дана еще в XVIII веке Лагранжем в его классическом труде "Аналитическая механика".

Жозеф Луи Лагранж (1736 - 1813) - с 19-летнего возраста профессор математики в Турине. С 1759 года - член, а с 1766 года - президент Берлинской Академии наук; с 1787 года жил в Париже. В 1776 году был избран почетным иностранным членом Петербургской Академии наук.

В конце XIX века Рэлеем были заложены основы линейной теории колебаний систем с бесконечной степенью степеней свободы (т.е. с непрерывным распределением массы по всему объему деформируемой системы). В XX веке линейная теория, можно сказать, была завершена (метод Бубнова-Галеркина, который позволяет с помощью последовательных приближений определять также высшие частоты колебаниий).

Джон Уильям Стретт (лорд Рэлей) (1842 - 1919) - английский физик, автор ряда работ по теории колебаний.

Иван Григорьевич Бубнов (1872 - 1919) - один из основоположников строительной механики корабля. Профессор Петербургского политехнического института, с 1910 года - Морской академии.

Борис Григорьевич Галеркин (1871- 1945) - профессор Ленинградского политехнического института.

Формула Рэлея наиболее популярна в теории колебаний и устойчивости упругих систем. Идея, лежащая в основе вывода формулы Рэлея, сводится к следующему. При моногармонических (однотонных) свободных колебаниях упругой системы с частотой w, перемещения ее точек совершаются во времени по гармоническому закону:

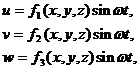
где ¦₁(x,y,z), ¦₂(x,y,z), ¦₃(x,y,z) - функции пространственных координат точки, определяющие рассматриваемую форму колебаний (амплитудную).

Если эти функции известны, то частоту w свободных колебаний можно найти из условия постоянства суммы кинетической и потенциальной энергии тела. Это условие приводит к уравнению, содержащему лишь одну неизвестную величину w.

Однако указанные функции заранее неизвестны. Руководящая идея метода Рэлея состоит в том, чтобы задаваться этими функциями, сообразуя их выбор с граничными условиями и ожидаемой формой колебаний.

Подробнее рассмотрим реализацию этой идеи для плоских изгибных колебаний стержня, форма колебаний описывается функцией ¦=¦(x). Свободные колебания описываются зависимостью

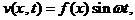(33)

потенциальная энергия изогнутого стержня

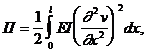(34)

кинетическая энергия

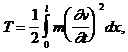(35)

где l - длина стержня, m=m(x) интенсивность распределенной массы стержня;

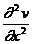- кривизна изогнутой оси стержня; 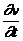- скорость поперечных колебаний.

Учитывая (33)

.

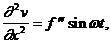
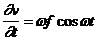Тогда

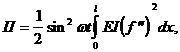(36)

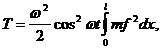(37)

С течением времени каждая из этих величин непрерывно меняется, но, согласно закону сохранения энергии их сумма остается постоянной, т.е.

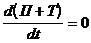(38)

или подставляя сюда выражения (36), (37)

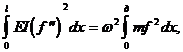(39)

Отсюда следует формула Рэлея:

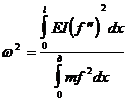(40)

Если со стержнем с распределенной массой m, связаны сосредоточенные грузы с массами M_i, то формула Рэлея приобретает вид:

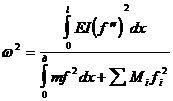(41)

Как относиться к этой формуле - считать ее точной или приближенной?

Весь ход вывода показывает, что в рамках принятых допущений (справедливость технической теории изгиба стержней, отсутствия неупругих сопротивлений) эта формула точная, если ¦(x) - истинная форма колебаний. Однако функция ¦(x) заранее неизвестна. Практическое значение формулы Рэлея состоит в том, что с ее помощью можно найти собственную частоту w, задаваясь формой колебаний ¦(x). При этом в решение вностися более или менее серьезный элемент приближенности. По этой причине формулу Рэлея иногда называют приближенной.

Пример:

y

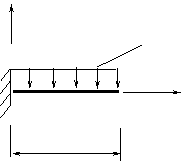m=cosnt Примем в качестве формы колебаний функцию: ¦(x)=ax², которая удовлетворяет кинематическим граничным условиям задачи.

x

EI

l

Определяем:

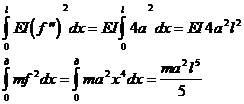
По формуле (40)

.

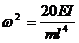Этот результат значительно отличается от точного

.

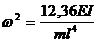Более точной является формула Граммеля, которая до сих пор еще не стала такой популярной, как формула Рэлея (возможно, вследствие своей относительной "молодости" - она предложена в 1939 году).

Снова остановимся на той же задаче о свободных изгибных колебаниях стержня.

Пусть ¦(x) - задаваемая форма свободных колебаний стержня. Тогда интенсивность максимальных сил инерции определяется выражением mw²¦, где по прежнему m=m(x) - интенсивность распределенной массы стержня; w² - квадрат собственной частоты. Эти силы достигают указанного значения в тот момент, когда прогибы максимальны, т.е. определяются функцией ¦(x).

Запишем выражение наибольшей потенциальной энергии изгиба через изгибающие моменты, вызываемые максимальными силами инерции:

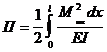. (42)

Здесь 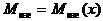- изгибающие моменты, вызываемые нагрузкой mw²¦. Обозначим 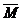_изг - изгибающий момент, вызываемый условной нагрузкой m¦, т.е. в w² раз меньший, чем силы инерции.

Тогда:

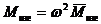, (43)

и выражение (10) можно записать в виде:

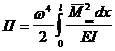. (44)

Наибольшая кинетическая энергия, как и выше

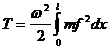(45)

Приравнивая выражения (44) и (45) приходим к формуле Граммеля:

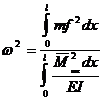(36)

Для вычислений по этой формуле необходимо прежде всего задаться подходящей функцией ¦(x). После этого определяется условная нагрузка m¦=m(x)¦(x) и записываются выражения 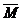_изг вызываемые условной нагрузкой m¦. По формуле (36) определяют частоту собственных колебаний системы w .

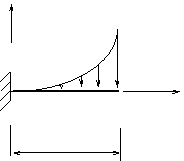
Пример: (рассматриваем предыдущий)

Условная нагрузка: m(x)=m=const; ¦(x)=ax²

y

m(x)·¦(x)=max²

x

EI

l

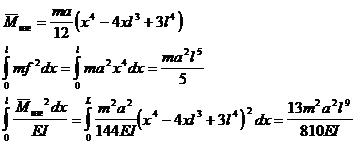
Находим: